季度降水分布函数的对比分析——以宜宾市为例

张 静, 倪长健, 袁淑杰

(成都信息工程学院高原大气与环境四川省重点实验室,四川成都610225)

降水是地面观测中最基本的气象要素之一,也是决定某地天气气候特征的关键因子[1]。它不仅直接影响土壤水分平衡,也间接影响太阳辐射、气温、湿度等天气变量。对降水量及其分布规律的研究不仅有重要的气候学意义,而且对农业生产以及水资源的合理调度都具有一定的指导意义。近年来,科学工作者开展了大量的相关研究工作。胡文东[2]指出宁夏大多数气象站的年降水量服从正态分布,而季度降水量及月降水量服从正态分布的气象站相对较少。吴慧[3]指出海南省各站春、夏、秋季降水基本符合正态分布,冬季仅北部和东部地区符合正态分布,月降水量的正态性也随季节而变化,且具有局地性。李伟光等[4]对海口不同时间尺度降水量进行了分布拟合,指出Γ分布函数对海口不同时间尺度降水量均有较好拟合效果。在气象变量中,干旱地区的年、季、月降水量,各种时段的最大降水量,最大风速和极大风速比较接近皮尔逊-Ⅲ(P-Ⅲ)分布[5]。以上研究表明,在不同地区及不同的时间尺度下,降水量服从不同的概率分布函数。

利用1960～2010年宜宾地区日降水量资料,基于正态分布、对数正态分布、伽马分布及皮尔逊-Ⅲ分布函数进行宜宾季度降水量拟合分布研究。在此基础上,基于离差最小平方和准则探讨各季降水量的最优分布函数,以期为农业生产、水资源管理与应用以及防灾、减灾提供一定的科学依据。

1 分布函数及参数估计方法

大多数诊断方法和预测模型都是建立在假设气候变量是正态分布的前提下进行的,但气候变量并不都符合正态分布,从这个意义上讲,对于气候变量分布函数的研究还有助于提高气候诊断预报的准确性。在前人研究成果的基础上,文中选择正态分布函数、对数正态分布函数、伽马函数及皮尔逊-Ⅲ分布函数进行宜宾市各季度降水量分布拟合研究。

1.1 分布函数的选择

正态分布作为最常见且应用最广泛的随机变量的分布,在随机变量的分布中居于中心地位[6],其概率密度函数为:

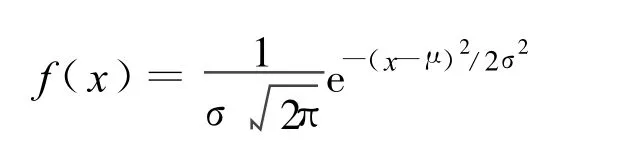
式中,μ、σ分别为正态分布变量的均值和标准差。

两参数对数正态分布是常见的一种用来描述正态分布的有偏数据的分布,被广泛地应用于经济、医学、生物和材料等研究领域。对于 x＞0,其概率密度函数为:

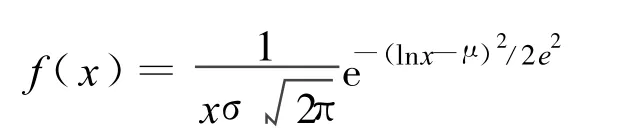
式中,μ、σ分别为变量对数值的平均值与标准差。

伽马分布模式是统计学基本模式之一,伽马分布有较强的适应性,可以拟合许多正偏的观测资料,因此在统计气候学,环境污染,人工控制天气等方面被广泛应用。其概率密度函数为:

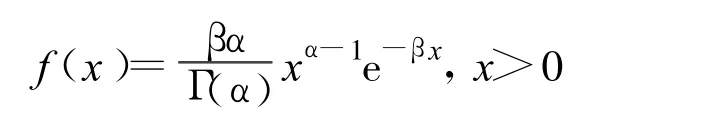
其中,α为伽马分布的形状参数,α＞0;β为伽马分布的尺度参数,β＞0。

P-Ⅲ型分布常用于拟合水文变量分布,其概率密度函数为

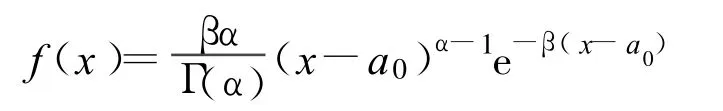
式中,Γ(α)为 α的伽马函数;α、β、a0分别是P-III型分布函数的形状、尺度和位置参数,α＞0,β＞0。

1.2 各分布参数估计方法

极大似然估计方法是参数估计中最重要、应用最广泛的方法之一,选取使似然函数达到最大的数值作为参数的估计值。正态分布函数、对数正态分布函数及伽马分布分别采用极大似然法进行参数估计[4,7-8]。由前人的研究成果表明,概率权重法用于P-Ⅲ分布的参数估计时,其稳定性优于其他方法,因此,文中亦选用此方法进行P-Ⅲ分布的参数估计[9]。

1.3 拟合检验方法

对于气候要素概率分布拟合试验,可选用任何理论分布函数,但只有通过拟合检验的分布函数,最终才能用于该气候要素分布的拟合。常用于拟合检验的方法有 χ2检验和Kolmogorov-Smirnov检验。文中选用K-S检验[10]进行分布函数的拟合。对通过拟合检验的分布函数,基于离差最小平方和准则(OLS)[11],优选出拟合各季度降水最优的分布函数。

2 应用实例

利用1960～2010年季降水量资料,分别应用正态分布、对数正态分布、伽马分布及P-III型分布函数进行宜宾各季降水分布拟合研究。首先,根据参数估计法求得的参数构建出各季度降水量的分布模型。

通过得到的分布模型及实测降水概率曲线,得到宜宾市各个季度分布函数拟合图如图1～4所示。从图中可以看出,不同分布函数对降水量的拟合效果不同。其中,P-III型分布函数的拟合效果相对较好,其理论频数与实测频数的吻合程度相当高。相比而言,其余3种分布曲线与实测曲线的吻合度相对较低,但和实测曲线的走势基本一致。就同一分布函数而言,其对不同季节降水量的拟合效果也存在差异。如P-Ⅲ分布和Г分布对秋季降水量的实测频数曲线吻合度较高,而其他季节吻合度相对较低,拟合效果相对较差;而对数正态分布则与春季和冬季降水量的实测频数曲线较为吻合,说明这两个季节的拟合效果相对较好;正态分布则对春季及秋季降水量的拟合效果较差。除此之外,各分布对不同季节下不同降水量级的拟合程度也存在差异。春季,正态分布对降水量为80～120mm及200～360mm降水量级的频数曲线拟合较差,而对120～200mm降水量的频数曲线拟合较好;夏季,Г分布及对数正态分布与420～600mm降水量级下的实测频数曲线吻合较差;秋季,4种分布函数对降水量级为200～400mm的实测频率曲线相对拟合较差;冬季,Г分布和对数正态分布对降水区间在50～70mm的实测频数曲线拟合较差。

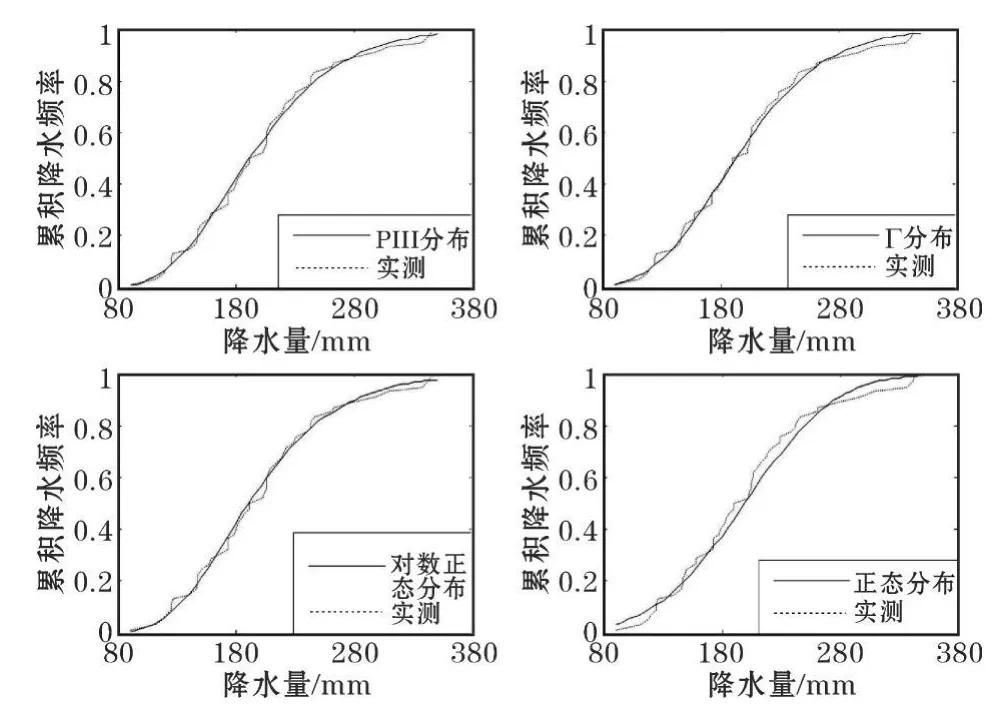
图1 春季各分布函数的拟合图对比

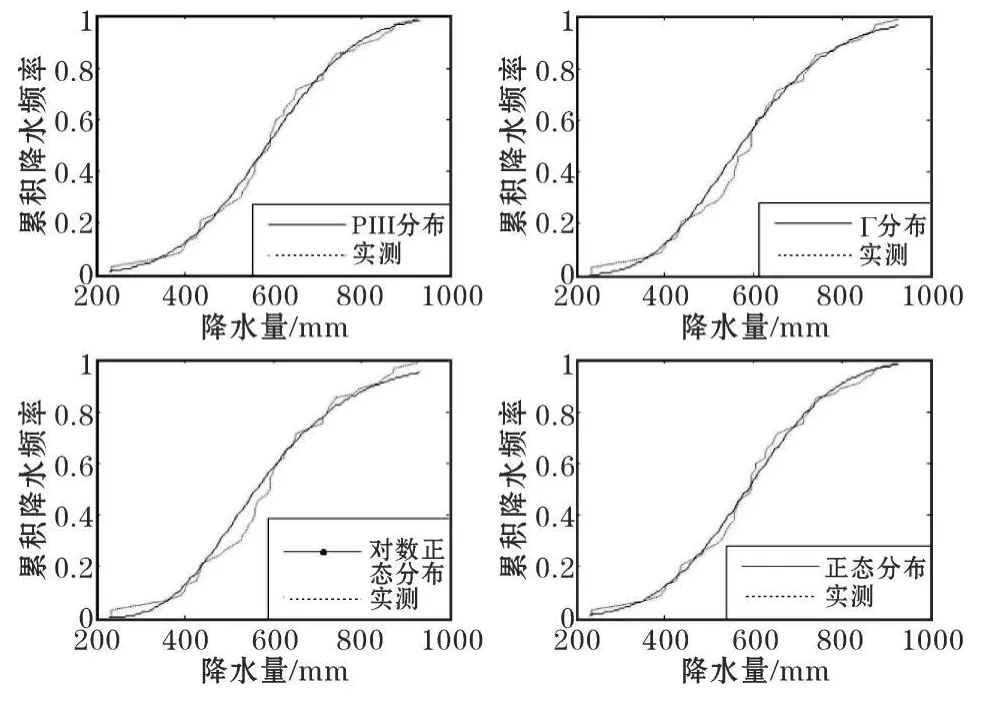
图2 夏季各分布函数的拟合图对比

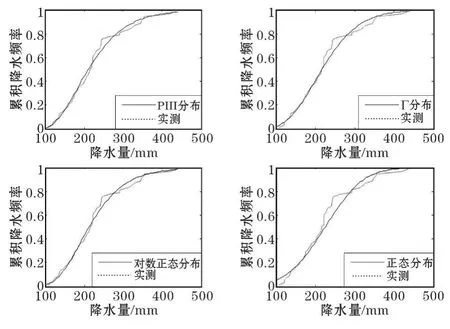
图3 秋季各分布函数的拟合图对比

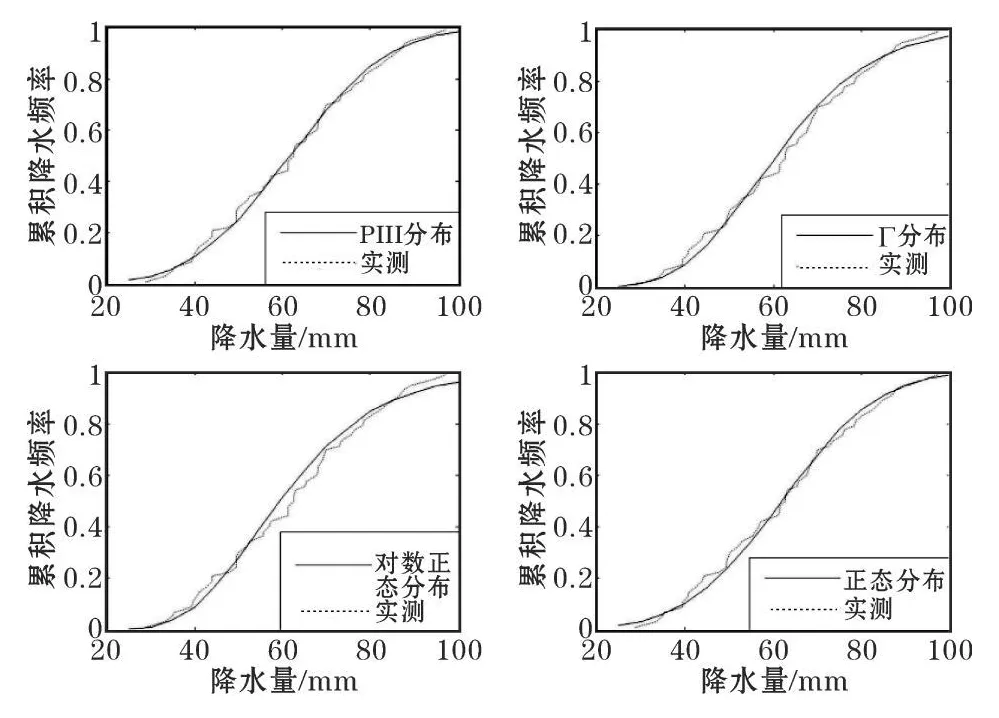
图4 冬季各分布函数的拟合图对比

2.1 拟合检验

从图1～图4可知,正态分布、伽马分布、对数正态分布及P-Ⅲ分布函数对宜宾市季度降水量的实测曲线基本吻合。但若要将上述分布用于宜宾市季度降水量的拟合中,则还需对分布函数进行拟合检验。对于K-S检验,当其统计量Dn小于临界值Dαn时,则表示通过检验。文中选取置信水平 α=0.05,当统计样本数 n=51时,查表得临界值Dαn=0.18659,若实际降水资料拟合概率分布的Dn＜Dαn,则说明拟合概率分布模型通过95%的置信度检验。根据各季度降水资料及各分布函数模型,计算出的K-S检验统计量如表1所示。从表1可知,对于4种概率分布函数,均存在Dn＜Dαn。说明4种理论分布均通过检验,即宜宾市季度降水量均可用正态分布、伽马分布、对数正态分布和P-Ⅲ分布函数进行拟合。虽然各分布都通过拟合检验,但由于其K-S值不一样,各分布的检验效果也存在一定的差异。如夏季对数正态分布函数、秋季的正态分布函数和Г分布、冬季的对数正态分布函数的Dn＞0.1,相对而言,上述几种情况的分布函数对实测曲线的拟合效果更差。

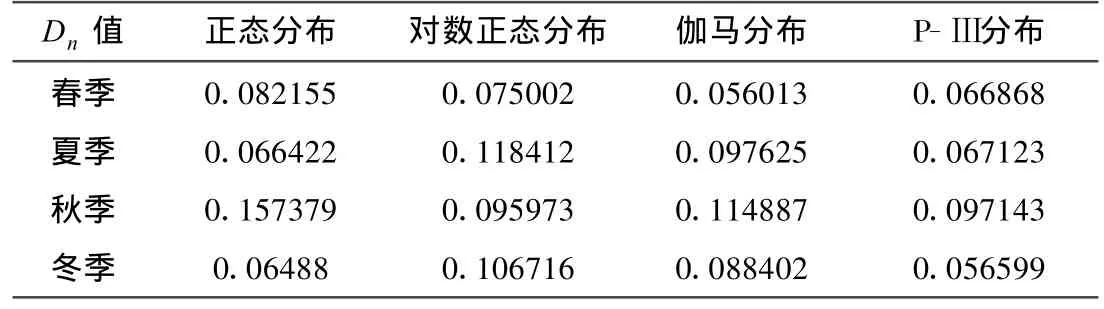
表1 各季4种分布的K-S检验计算结果

2.2 对比分析

从拟合图及K-S的检验结果可知,各分布函数均可用于宜宾市各季降水量的拟合,同时,拟合效果也存在一定的差异。春季,除正态分布外,其余3种分布函数对实测曲线的拟合效果都较好;夏季,P-Ⅲ分布及正态分布的拟合效果相对较好;秋季,P-Ⅲ分布及对数正态分布的拟合效果相对较好;而冬季,P-Ⅲ分布、伽马分布和正态分布拟合效果都较好。针对这些差异,为了进一步判定宜宾市各季降水量的最优拟合分布函数,通过OLS准则进行宜宾各季降水量拟合的最佳分布函数分析。当OLS值最小,则其对应的分布就为拟合效果最佳的分布。

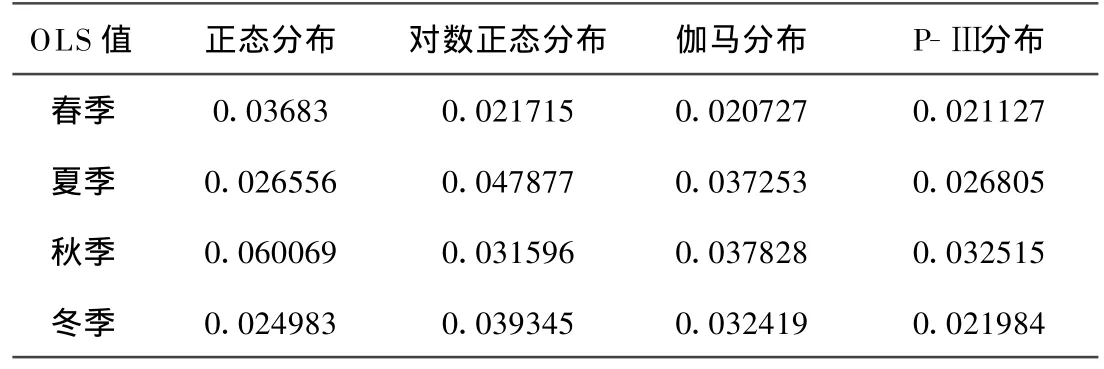
表2 各概率分布函数OLS方法计算结果

从表2看出:春季,伽马分布的OLS值最小,说明在4种分布中,其能最好的拟合春季降水量分布;夏季,则是正态分布的理论曲线和实测分布曲线拟合的效果最好;对数正态分布则是对秋季降水量的最优拟合分布函数;而冬季则是P-Ⅲ分布函数的拟合效果最好。

总体而言,从拟合图、K-S检验及OLS拟合优度检验结果中可知,各分布函数对实测降水曲线的拟合效果较好,但各分布的拟合效果也存在着一定的差异。同时,从3种拟合结果中得出的差异都较为一致,如春季,从拟合图中可知正态分布的拟合效果最差,而其K-S检验结果也是最差的,同时,其OLS值最大,也说明该分布的拟合效果最差。

3 结论

根据四川省宜宾市的季度降水量资料,利用极大似然估计等参数估计方法,分别采用正态分布、伽马分布、对数正态分布和P-Ⅲ分布进行宜宾季度降水量最优拟合分布研究,得到以下主要结论:

(1)正态分布、伽马分布、对数正态分布及P-Ⅲ分布均可拟合宜宾市的各季降水量分布。

(2)通过对比分析可知,各季度降水量的最优拟合分布函数不同。伽马分布、正态分布、对数正态分布及P-Ⅲ分布分别为宜宾市春、夏、秋、冬各季降水量的最优拟合分布函数。这一结果与一般情况下认为P-Ⅲ分布为降水量拟合效果最优分布函数的结论不太一致。

因此,为了预报的准确性,对特征变量的最优拟合分布函数的研究很有必要,同时,对不同时间尺度降水量分布函数的研究也能进一步为农业生产提供一定的指导依据。

[1] 王纪军,任国玉,匡晓燕,等.河南省月和年降水量正态性分析[J].气候与环境研究,2010,15(4):522-528.

[2] 胡文东,陈晓光,李艳春,等.宁夏月、季、年降水量正态性分析[C].2007年中国气象学会年会论文集,2007:1036-1044.

[3] 吴慧.海南省降水量的正态分布特征及正态化变换[J].广东气象,2005,(2):12-13.

[4] 李伟光,朱乃海,陈汇林,等.海口不同时间尺度降水量统计拟合[J].安徽农学通报,2007,13(12):189-190,227.

[5] 屠其璞,王俊德,丁裕国,等.气象应用概率统计学[M].北京:气象出版社,1984.

[6] 罗春玲.正态分布的性质及应用[J].才智,2010,17:64-66.

[7] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2001:179-185.

[8] 于洋,孙月静.对数正态分布参数的最大似然估计[J].九江学院学报,2007,26(6):55-57.

[9] 宋德敦,丁晶.概率权重矩法及其在P-III分布中的应用[J].水利学报.1988,(3):1-11.

[10] 侯芸芸.基于Copula函数的多变量洪水频率计算研究[D].西安:西北农林科技大学,2010.

[11] 郭生练,闫宝伟,肖义,等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文,2008,28(3):1-7.

[12] 谢华,黄介生.两变量水文频率分布模型研究述评[J].水科学进展,2008,19(3):443-452.