热薄型材料复印纸点燃模型的试验研究

吴桂红 ，吴义强 ，胡云楚 ，袁利萍 ，姚春花

(1.中南林业科技大学 a.材料科学与工程学院，1b. 理学院，湖南 长沙 410004；2. 竹业湖南省工程研究中心，湖南 长沙 410004)

热薄型材料复印纸点燃模型的试验研究

吴桂红1a，1b，吴义强1a，2，胡云楚1a，1b，袁利萍1a，姚春花1a

(1.中南林业科技大学 a.材料科学与工程学院，1b. 理学院，湖南 长沙 410004；2. 竹业湖南省工程研究中心，湖南 长沙 410004)

热薄型材料相比热厚型材料在火灾初期更易点燃，因此研究热薄型材料的点燃对于预防火灾的发生及蔓延具有重要意义。利用锥形量热仪以复印纸为试样进行了试验测试，得到试样在不同热辐射强度下的点燃时间，并将试验结果与之前的理论模型进行对比验证。试验结果更符合线性热损失的点燃模型，该模型还提供了临界辐射热通量的计算公式，其数值和试验值相吻合。线性热损失的点燃模型可用来预测热薄型材料在不同热辐射强度下的点燃时间。

热薄型材料；复印纸；点燃模型；点燃时间；临界辐射热通量

火灾的发生始于材料的点燃，火蔓延即是材料不断被点燃的过程。在热源作用下热薄型材料相比热厚性材料更容易被点燃，燃烧释放出热量再引燃周围的可燃物，如果失去人为控制就可能引发大的火灾。因此，研究热薄型材料的点燃对于预防火灾的发生及蔓延具有重要意义。Spearpoint[1]利用积分模型研究不同热辐射情况下材料的点燃，分析机理并提出了点燃时间的计算模型；Spearpoint提出了临界热流的概念，认为如果达不到临界热流着火将不会发生，因此临界热流成为判断材料是否着火的重要判据。Mikkola和Wichman[2]将材料暴露表面的边界条件简化为热辐射边界，运用拉普拉斯变换方法，推导得到热厚型、热薄型材料点燃时间的理论计算公式。Delichatsios[3]则认为点燃模型应根据辐射量的不同而采用不同的模型，有热薄型、热厚型和有限厚度模型之分。国内外学者从理论到试验对不同工况下不同材料的点燃模型做了系列研究[4-12]，研究结果表明，热厚型材料的点燃时间平方根的倒数与热流强度具有近似的线性关系，热薄型材料引燃时间的倒数与外辐射热通量具有很好的线性关系。

1 研究方法

1.1 燃烧性能测试仪器及样品

试验样品为浙江广博集团股份有限公司生产的嵩山多功能复印纸（NO.F7041），试样尺寸为100 mm×100 mm。为了减少外界的影响，将样品放在用铝箔纸包覆的100 mm×100 mm×10 mm岩棉板上进行隔热，背面垫有厚13 mm、密度为650 kg/m3、热阻很大的矿棉纤维毯，保证符合背面隔热的条件。

采用英国FTT锥形量热仪，按照ISO 5660标准试验方法，测试样品在预先设定的不同热辐射强度下的点燃时间，每种工况下重复3次。

1.2 热薄型材料的点燃模型

固体材料的厚度对其传热行为有着重要的影响，根据不同厚度条件下材料传热行为的不同表现，可将固体材料分为热薄型材料和热厚型材料。热薄型材料是指与固体材料中热扩散层的特征厚度相比，材料厚度相对较小，沿厚度方向所观察到的固体性状无明显变化，因此可以把热薄型材料固体内部温度看成一个值，且与表面的温度相同，即固体内部的温度只是时间坐标的函数，而不是空间厚度坐标的函数，而热厚型材料内部则存在温度梯度。热薄型对应的情况之一就是物理尺寸很薄的材料受热，比如说薄膜、纸张、布匹、薄木等。一般来说，厚度不超过1 mm的材料都可视为热薄型，故试验样品复印纸可以视为热薄型材料。

热薄型理想材料受热模型请参见笔者之前的论文[13]，并在无热损失和线性热损失两种情况下分别得到了相应的点燃模型

式 中tig为 点 燃 时 间，I为 热 辐 射强 度，C为 热 容 量，α 为 吸 收 比，Tig为点燃温度，T0为室温，ht为表面总的换热系 数； 而 合 并 系 数 C1=[C(Tig-T0)]/α，C2=C/ht和C3=[ht(Tig-T0)]/α都可通过软件自定义函数拟合计算得到。

式（2）从数学意义上来讲要有意义就必须满足I＞C3，其物理意义就是体现了不同工况下试样的点燃必须达到一定的引燃临界热流，而临界热流是判断材料是否能够发生着火的重要判据。只有当外加辐射热流大于临界辐射热通量时，试样才会被点燃。由式（2）可以得到引燃临界辐射热通量CHF=C3=[ht(Tig-T0)]/α，试样总的换热系数、吸收比、点燃温度等都是随实际火灾工况变化的，利用查到的相关数据代入近似估算，可以确定CHF的数量级应为103～104。

2 结果及分析

2.1 试验结果

利用英国FTT锥形量热仪测定了预先设定的不同的热辐射强度下复印纸的点燃时间，试验数据列于表1。

表1 不同热辐射强度下复印纸的点燃时间Table 1 Ignited time of copy paper under different radiation intensity

试验还测定了较低热流下的情况，虽然在较低热流下试样不燃或阴燃，但这些数据在确定拟合参量初值以及判定临界热流时需考虑，具体试验结果列于表2。

表 2 低于临界热辐射通量下复印纸的点燃情况Table 2 Ignited situations of copy papers with below critical heat flux

2.2 两种模型的拟合对比

取三次同等工况下试验的平均值作为拟合数据，分别按照无热损失的点燃模型的式（1）和线性热损失的点燃模型的式（2）进行自定义函数拟合，得到两个相应的数值拟合模型

对比线性热损失的理论点燃模型的式（2）和数值拟合模型的式（4）可以得到CHF=C3=2.468 435 164×104W/m2。一方面，这与前面CHF估算的数量级103～104是相符的；另一方面，这与试验结果也是相符合的，试验中在辐射热流为 2.25×104W/m2时不燃，2.5×104W/m2时点燃时间为87.7 s，所以临界辐射热通量应在2.25×104～2.5×104W/m2之间，这与式（4）中CHF=2.468 435 164×104正好吻合。最重要的是，线性热损失的点燃模型可以很清晰地体现出引燃的临界辐射热通量的物理含义，这也正是采用该模型的最大的优越之处。

两个模型的拟合曲线图与试验结果对比见图1，图中横轴为热辐射强度，纵轴为点燃时间。两条拟合曲线都体现了点燃时间随着热辐射强度的增大而减小；结合拟合图形以及拟合报表可以得到结论：在整个试验范围内线性热损失的点燃模型的拟合效果明显优于无热损失的点燃模型。复印纸放在用铝箔纸包覆的岩棉板上，背面垫有矿棉纤维毯，希望能够满足背面隔热的条件，只是背面完全隔热的条件在实际火场或是试验中尤其是高热流强度下是很难满足的，毕竟热损失在大多数加热情况下都不可能完全忽略不计的。线性热损失的点燃模型的拟合曲线尾部稍有翘起，分析原因应该是试验误差引起的，随着辐射强度的增大，点燃时间越来越短，短到只有三四秒的时候试验误差引起的相对误差就会比较大。从实际意义出发应重点关注热流范围为20～40 kW/m2，毕竟当材料的点燃时间随着辐射强度的增加而减小到短暂的2秒或是3秒已没有太多实际的应用价值。

图1 复印纸的点燃时间与辐射强度的拟合对比曲线Fig.1 Fitting curves between ignited time and radiation intensity of copy paper

2.3 点燃时间倒数模型的对比检验

为了检验模型的可靠性，可将拟合结果与Mikkola＆Wichman[2]推导得到的热薄型材料点燃时间的理论计算公式进行对比，该理论公式为：

这表明了热薄型材料引燃时间的倒数与外辐射热通量具有很好的线性关系，不少学者的试验研究结果也证明了这一结论。

同样，将式（1）和（2）分别求点燃时间的倒数，可得到

利用试验结果结合式（6）、（7）和（8）分别作3个模型的点燃时间倒数对辐射热通量的拟合曲线图，并与试验结果对比见图2，图中横轴为热辐射强度，纵轴为点燃时间的倒数。图2显示出，利用试验数据按Mikkola & Wichman理论模型和线性热损失的点燃模型拟合出来的效果都是很不错的，而无热损失的点燃模型的拟合效果相对欠佳，这与前面的理论分析也是相吻合的。当辐射强度从30 kW/m2到45 kW/m2，线性热损失的点燃模型的拟合效果较理想，在30 kW/m2处很明显地体现出引燃的临界辐射热通量，只是数值与前面的试验结果（25、27.5 kW/m2）不同，分析原因是由于数值模拟的精度数量级的差异造成的，于是针对同数量级也即是前三组试验数据再进行了相应的模拟，得到模拟对比图3。图3显示出对于辐射强度为25、27.5 和30 kW/m2时，线性热损失的点燃模型和Mikkola & Wichman理论模型都有很好的拟合效果。一方面这说明了对于热薄型材料的点燃时间倒数与辐射强度成正比是成立的，另一方面也验证了利用线性热损失的点燃模型来模拟是基本可行的，同时该模型还能清晰地体现临界热辐射强度的意义。在图3中得到的CHF= 2.468 435 164×104W/m2，这与前面线性热损失数值拟合模型式（4）得到的CHF=C3= 2.468 435 164 ×104W/m2也是相吻合的，这也再次验证了线性热损失的点燃模型的可行性。

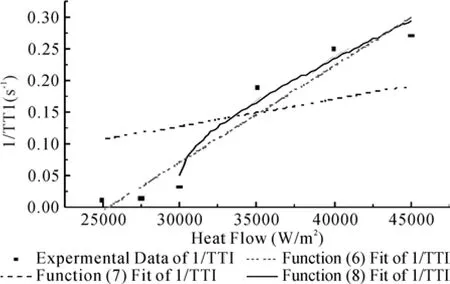
图2 3个模型的点燃时间倒数的对比拟合曲线Fig.2 Fitting curves of inverse of ignited time among three models

图3 25、27.5 和30 kW /m2时3个模型点燃时间倒数的对比拟合曲线Fig.3 Fitting curves of inverse of ignited time among three models under conditions of 25, 27.5 and 30 kW /m2

3 结 论

利用锥形量热仪测试了复印纸在不同热辐射强度下的点燃时间，并用试验结果按照[13]文中建立的两种理论模型（即热薄型材料在无热损失和线性热损失两种条件下的点燃模型）分别进行拟合，得到了相应的数值模型。通过对比拟合效果的优劣来反证理论模型的优劣，线性热损失的点燃模型比起无热损失的模型更符合试验结果，理论分析与试验结果达到一致。实际问题中，材料的受热是非常复杂的过程，光有理论分析或是试验结果都是远远不够的，二者有效地结合起来考虑更具可行性，也更具可信度。另外，考虑线性热损失的点燃模型最大的优越之处就是能够清晰地体现出临界热辐射通量的物理意义。将两种模型的点燃时间倒数拟合图与Mikkola & Wichman理论模型进行了对比，验证了考虑热损失模型的可行性和优越性。线性热损失的点燃模型可用来预测材料在不同热辐射强度下的点燃时间，为材料的制造及其应用提供阻燃防火的科学理论指导。

[1] Spearpoint M J. Predicting the ignition and burning rate of wood in the cone calorimeter using an integral model [M]. Baltimore:University of Maryland, 1999.

[2] Mikkola E, Wichman I. On the thermal ignition of combustible materials [J].Fire and Materials, 1989, 14: 87- 96.

[3] Delichatsios M A. Ignition time for thermally thick and intermediate conditions in flat and cylindrical geometries [J]. Fire Science and Technology Laboratory, 1995, 102(3): 233-244.

[4] Babrauskas V, Wetterlund I. Testing of furniture composites in the cone calorimeter: a new specimen preparation method and round robin results [J].Fire Safety Journal, 1998, 30: 179 -194.

[5] Nazaré S, Kandola B, Horrocks A R. Use of cone calorimetry to quantify the burning hazard of apparel fabrics [J].Fire and Materials, 2002, 26:191-199.

[6] Woodfield P L, Monde M, Mitsutake Y. Improved analytical solution for inverse heat conduction problems on thermally thick and semi-infinite solids[J]. International Journal of Heat and Mass Transfer, 2006, 49: 2864-2876.

[7] Lee B H, Kim H S, Kim S, et al. Evaluating the flammability of woodbased panels and gypsum particleboard using a cone calorimeter[J].Construction and Building Materials, 2011,25:3044-3050.

[8] Spearpoint M J, Quintiere J G. Predicting the piloted ignition of wood in the cone calorimeter using an integral model-effect of species, grain orientation and heat flux [J]. Fire Safety Journal,2001, 36:391-415.

[9] Schartel B,Hull T R. Development of fire-retarded materials-Interpretation of cone calorimeter data [J]. Fire and Materials,2007, 31:327-354.

[10] Hapuarachchi T D, Ren G, Fan M, et al. Fire retardancy of natural fibre reinforced sheet moulding compound [J]. Appl Compos Mater, 2007, 14:251-264.

[11] Delichatsios M A. Piloted ignition times, critical heat fluxes and mass loss rates at reduced oxygen atmospheres [J]. Fire Safety Journal, 2005, 40: 197-212.

[12] Wang Yafei, Yang Lizhong, Zhou Xiaodong, et al. Experiment study of the altitude effects on spontaneous ignition characteristics of wood [J]. Fuel, 2010, 89: 1029-1034.

[13] 吴桂红,吴义强,胡云楚,等. 热薄型材料在均匀辐射场中的点燃模型[J]. 中南林业科技大学学报,2012,32(1):14-17.

Experimental study on ignition models of thermally thin material (copy paper)

WU Gui-hong1a,1b, WU Yi-qiang1a,2, HU Yun-chu1a,1b, YUAN Li-ping1a, YAO Chun-hua1a

(1a. School of Materials Science and Engineering; 1b. School of Science, Central South University of Forestry and Technology, Changsha 410004, Hunan, China; 2. Hunan Provincial Engineering Research Center of Bamboo Industry, Changsha 410004, Hunan, China)

∶ Thermally thin material is more easily ignited than thermally thick material does in the initial stage of fire disaster, so studying the ignition models of thermally thin material has important significance to preventing fire. Cone calorimeter (CONE) was used to test the ignited time of copy papers in different heat fluxes. And the tested ignited time was contrasted with that computered by the theoretical models. The ignition model of linear processing heat loss was well consistent with the test result,which can provide the calculating formula of critical heat flux, and the the calculated values and experimental values coincided very well. Therefore, the ignition model of linear processing heat loss can be used to predict the ignited time of thermally thin material under different heat radiation intensity.

∶ thermal thin materials; copy paper; ignition model; ignited time; critical heat flux

S784；TK16

A

1673-923X(2013)11-0162-04

2013-08-16

国家自然科学基金项目(31170521)；高等学校博士学科点专项科研基金资助课题 (20114321110005)

吴桂红（1979-），女，讲师，博士研究生，主要从事物理学和生物质复合材料研究；E-mail: guihongwu@163.com

胡云楚（1960-），男，湖南湘潭人，教授，博士，博士生导师，主要从事材料化学和阻燃材料方面的研究；E-mail:hucsfu@163.com；吴义强（1967-），男，河南固始人，教授，博士，博士生导师，主要从事木材科学、木材功能性改良、生物质复合材料研究，E-mail: wuyq0506@126.com

[本文编校：吴 毅]