Multiple solutions and fermion mass effect in QED3
Zhou Yuqing
(Department of Physics, Southeast University, Nanjing 211189, China)
Nowadays, it is widely accepted that quantum chromodynamics (QCD) in 3+1 dimensions is a basic theory for hadron physics. Especially in high energy regions, the theoretical results of QCD coincide with the corresponding hadron experiment. However, QCD is very difficult to deal with in the low-energy region because here the nonperturbative effects cannot be ignored. In addition, since the full propagators including high-order corrections contain all the physical information about QCD, the theoretical results depend on the form of the propagators. Up to now, the investigation of the propagators in low energy is still a challenging domain in field theory. Using the Lorenz analysis, we write the inverse quark propagator as

whereAq(m,p2) is the vector part andBq(m,p2) is the scaler part. As is well known, there are two solutions to the Dyson-Schwinger equation (DSE) for the quark propagator, i.e. the Numbu-Goldstone (NG) solution and the Wigner (WN) solution. In chiral limit, the NG solution corresponds to the chirally broken phase while the WN solution corresponds to the chirally symmetric phase. One accepts that the NG solution is the solution realized in the real world. So the investigation of the NG solution is an interesting problem.

QED3as a field-theoretical model has been extensively studied in recent years. It has many features similar to quantum chromdynamics (QCD) in 3+1 dimensions. This is because QED3is known to have a phase where the initial chiral symmetry of the theory is spontaneously broken and it is also known that the fermions are confined in this phase. Moreover, QED3is superrenormalizable, so it is not plagued with the ultraviolet divergences which are present in QED4. These are the basic reasons why QED3is regarded as an interesting toy model. It is far more simple in theoretical structure to study color confinement and dynamical chiral symmetry breaking(DCSB)[4-7]by QED3than by QCD. Therefore, we can use the DSEs for the fermion and photon propagators in QED3to investigate our problems.
1 Dyson-Schwinger Equation for Fermion Propagator
The Lagrangian of QED3in a general covariant gauge in the Euclidean space, ignoring the issues discussed in Ref.[8], can be written as
(1)
where the 4×1 spinorψis the fermion field. In chiral limit,m=0; i.e., this Lagrangian is chiral symmetric. But the broken symmetry makes the fermion gain a nonzero mass due to the nonperturbative effect. Then the chiral phase transition occurs. The order parameter is trivially defined as
(2)
whereA(p2),B(p2) are obtained in the following. The infrared value ofB(p2) is also considered as the order parameter. Atm≠0, the last definition should be changed[9].
Generally, the fermion propagator with nonzero mass can be divided into two parts, the massless part and the mass part. We suppose that the inverse fermion propagator is analytic about fermion mass.
(3)
Atm→0, the high-order terms can be ignored. Based on the Lorentz analysis, the mass term in the last function is written as
(4)
We aim to obtain the involved four functions,A,B,C,D. The functions can be obtained by the application of the Dyson-schwinger (DS) equation for the fermion propagator. In chiral limit, the full inverse fermion propagator and the full photon propagator satisfy the following DS equation,

(5)

(6)
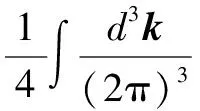
(7)
where the notation Tr denotes trace over the Dirac indices. If the coupled functions have nontrivial solutions (the NG solution,B(p2)≠0), then the original massless fermion will acquire nonzero mass and chiral symmetry is broken spontaneously.
In addition, the DS equation satisfied by the photon vacuum polarization tensor can be written as

(8)
Using the relationship between the vacuum polarizationΠ(q2) andΠρν(q2),
Πρν(q2)=(q2δρν-qρqν)Π(q2)
(9)
we can obtain an equation forΠ(q2) which has ultraviolet divergence. Fortunately, it is present only in the longitudinal part. One can remove this divergence by applying the projection operator

(10)
and obtain a finite vacuum polarization. However, the full vertex is unknown. Although several works have attempted to solve it[10-16], none of them have turned up trumps. Following some previous works[17-18], we choose the first part in theBCvertex,

(11)
One argues that this tenser destroys Ward-Takahashi identity(WTI), whereas self-consistent investigation (more details can be found in Ref.[8]) shows that numerical results of the DSE for the fermion propagator obtained by adopting this vertex are almost equivalent to those by the application ofBCandCPvertices[19]. Inspired by this, we choose the ansatze.
Finally, we have to choose a gauge. Since the Landau gauge is the most convenient and commonly used gauge, we use it. Using the rainbow approximation for the full vertex, the coupled DS equations for the fermion propagator and photon vacuum polarization reduce to the following form,
(12)
(13)
(14)
wherep=q+k.
The next step is to obtain mass functionsC(p2) andD(p2). In order to obtain the two functions, we start from propagators with massive fermion, where we will meetΓν(m;p,k). Since the Lagrangian of QED3is translation invariant, the WTI remains. We write the identity at small mass,
(p-k)νΓν(m;p,k)=S-1(p)-S-1(k)+m[Γ(p,0)-Γ(k,0)]
(15)
Based on the freeness of kinematic singularities, the vertex is given as
(16)

(17)
The corresponding boson propagator in Landau gauge can be written as
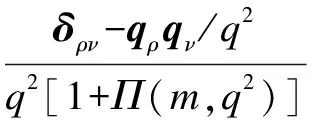
(18)
Based on the same idea for the fermion propagator, we also express this propagator asO(m1),

where

(19)
Substituting Eqs.(4) and (5) into the DS equation for the fermion propagator, we can obtain

(20)
and then obtain

(21)
From the DS equation of the fermion propagator atm≠0, ignoring the high order of massO(m2), we can obtain the linear part of fermion mass as follows:

(22)
The functions ofCandDare obtained as

(23)

(24)
And Boson polarization is also obtained in this approximation.



(25)
According to Eqs.(20) to (24) and using the identity

(26)
we obtain the coupled equations forC(p2),D(p2),Π′(q2),

whereH(k,q)=2k2-4kq-6(kq)2/q2. By all appearances, all the above three functions are not the functions of the fermion mass. From them, we will numerically investigateC(p2),D(p2),Π′(q2). It is noted that the three functions have no effect on our model in chiral limit.
2 Numerical Results
In chiral limit, we first define the original value of each function as a plus value to iterate, till the DS equations (11) to (13) obtain stable results. We plot them in Fig.1 and name this as a conventional or a plus solution. This solution was discussed in previous work[8].
Then, starting fromB<0, we also iterate the equation group to obtain a stable result and showA(p2),B(p2) andΠ(q2) in Fig.1. We can see from Fig.1 that the behaviors ofA(p2) orΠ(q2) are apparently different between the chirally symmetric phase and asymmetric phase, but are uniform whenB>0 andB<0.

Fig.1 Functions in the chirally symmetric phase and asymmetric phase. (a) A(p2); (b) B(p2); (c) Π(q2)
One sees that the function of fermion self-energy is negative at allp2and its absolute value is similar to a plus solution while the other two functionsA,Πdo not reveal different behaviors betweenB>0 andB<0. Then, settingB≡0, we numerically solve the coupled DS equations to obtain the Wigner solutions and they are also shown in Fig.1. The trivial solution of fermion self-energy lies betweenB<0 andB>0. However, correspondingA,Πreveal different behaviors whenB≠0. In infrared region,Adiminishes whenΠincreases and diverges whenp2→0.
Beyond chiral limit, we also study the linear effect of fermion mass on propagators. Using the above method, we obtainC(p2),D(p2) andΠ′(q2) as shown in Fig.2.
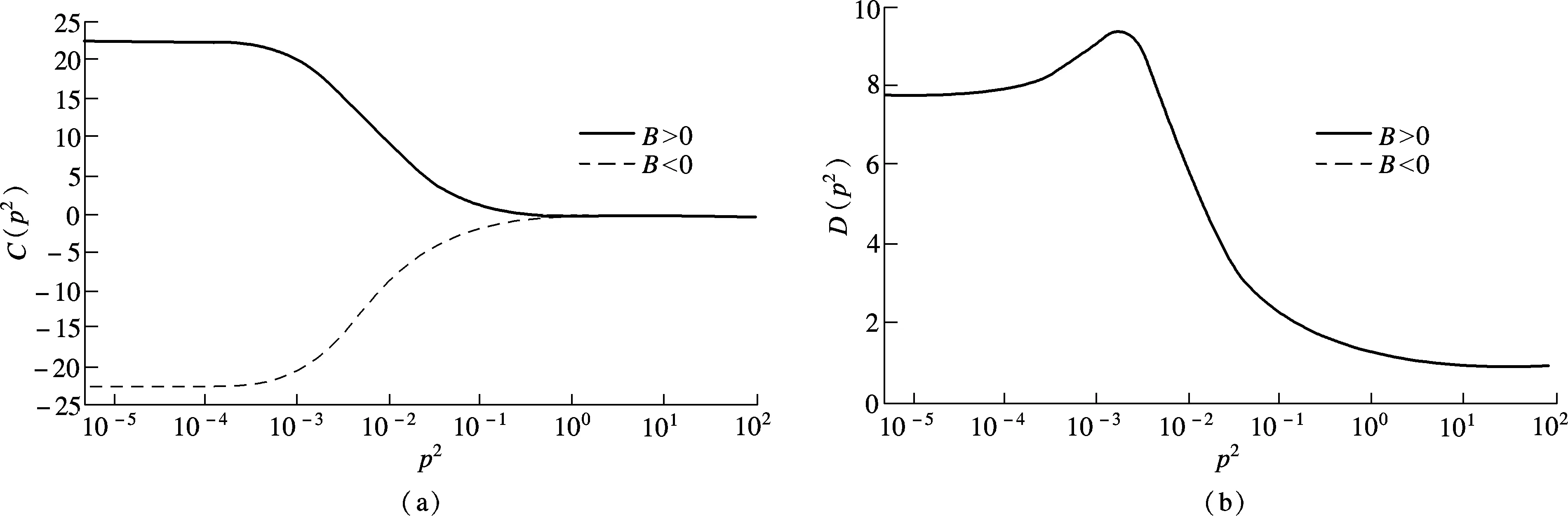

Fig.2 Functions in the broken phase. (a) C(p2); (b) D(p2); (c) Π′(q2)
One sees that there are two apparently different solutions forC(p2) andΠ′(q2), while we find only one solution forD(p2). All solutions for the three functions hardly change in the infrared region, but each value of the solutions diminishes in large momentum. WhenB>0 which is studied frequently in previous works, the DS equation gives the plus solution forC(p2) and negativeΠ′(q2). The infrared value of vector function of the fermion propagator decreases with the increasing mass. Nevertheless, forB<0, the second infrared value for vector function gives the opposite movement, and the difference between two infrared values gets large with the increasing mass.
In principle, there should be two solutions forD(p2), corresponding toC(p2),Π′(q2), while we only find one and it is plus. Therefore, the two scalar functions of the fermion propagator tend to equal each other and this is in accordance with Ref.[9] where QCD is used.
3 Conclusion
We have investigated the coupled DS equation for the fermion propagator in the unquenched QED3. In chiral limit, we find that, besides two familiar nonnegative solutions, there is a negative solution for this equation. Moreover, there exist two solutions for the DS equation beyond chiral limit. Since QED3may be relative to the theory of dx2-y2superconductivity, those solutions can be used to analyze the existence of three phases, antiferromagnet, pseudogap and superconductivity. We suppose that massless QED3is suitable in the underdoped region, especially near the area where the above mentioned three phases compete, and QED3with fermion mass does in the overdoped region in phase figure for YBCO.
AcknowledgementWe would like to thank Professors Zong Hongshi and Sun Weimin for helpful discussions.
[1]Burden C J, Praschifka J, Roberts C D. Photon polarization tensor and gauge dependence in three-dimensional quantum electrodynamics[J].PhysicalReviewD, 1992,46(6): 2695-2702.
[2]Grignani G, Semenoff G, Sodano P. Confinement-deconfinement transition in three-dimensional QED[J].PhysicalReviewD, 1996,53(12): 7157-7161.
[3]Maris P. Confinement and complex singularities in three-dimensional QED[J].PhysicalReviewD, 1995,52(10): 6087-6097.
[4]Cornwall J M. Confinement and chiral-symmetry breakdown: estimates ofFπand of effective quark masses[J].PhysicalReviewD, 1980,22(6): 1452-1468..
[5]Pisarski R D. Chiral-symmetry breaking in three-dimensional electrodynamics[J].PhysicalReviewD, 1984,29(6): 2423-2426.
[6]Appelquist T, Nash D, Wijewardhana L C R. Critical behavior in (2+1)-dimensional QED[J].PhysicalReviewLetters, 1988,60(25): 2575-2578.
[7]Nash D. Higher-order corrections in (2+1)-dimensional QED[J].PhysicalReviewLetters, 1989,62(26): 3024-3026.
[8]Maris P. Influence of the full vertex and vacuum polarization on the fermion propagator in (2+1)-dimensional QED[J].PhysicalReviewD, 1996,54(6): 4049-4058.
[9]Chang L, Liu Y X, Roberts C D, et al. Dynamical chiral symmetry breaking and a critical mass[J].PhysicalReviewC, 2007,75(1): 015201-01-015201-08.
[10]Pennington M R, Walsh D. Masses from nothing: a non-perturbative study of QED3[J].PhysicsLettersB, 1991,253(1): 246-251.
[11]Kondo K I, Nakatani H. Spontaneous chiral-symmetry breaking and scaling law in 3-dimensional QED[J].ModernPhysicsLettersA, 1990,5(6):407-416.
[12]Burden C J, Roberts C D. Light-cone regular vertex in three-dimensional quenched QED[J].PhysicalReviewD, 1991,44(2):540-550.
[13]Simmons E H. Useful gauges for studying dynamical fermion mass generation in arbitrary space-time dimension[J].PhysicalReviewD, 1990,42(8):2933-2935.
[14]Kondo K I, Maris P. First-order phase transition in three-dimensional QED with Chern-Simons term[J].PhysicalReviewLetters, 1995,74(1): 18-21.
[15]Gusynin V P, Hams A H, Reenders M. (2+1)-dimensional QED with dynamically massive fermions in vacuum polarization[J].PhysicalReviewD, 1996,53(4): 2227-2235.
[16]Burden C J, Tjiang P C. Deconstructing the vertex Ansatz in three-dimensional quantum electrodynamics[J].PhysicalReviewD, 1998,58(8): 085019-01-085019-08.
[17]Feng H T, Sun W M, Hu F, et al. The influence of the gauge boson mass on the critical number of the fermion flavors in QED3[J].InternationalJournalModernPhysicsA, 2005,20(13): 2753-2762.
[18]Feng H T, He D K, Sun W M, et al. Influence of finite chemical potential on the fermion chiral condensate in QED3[J].PhysicsLettersB, 2008,661(1): 57-65.
[19]Fischer C S, Alkofer R, Dahm T, et al. Dynamical chiral symmetry breaking in unquenched QED3[J].PhysicalReviewD, 2004,70(7): 073007-01-073007-20.
 Journal of Southeast University(English Edition)2013年4期
Journal of Southeast University(English Edition)2013年4期
- Journal of Southeast University(English Edition)的其它文章
- Elastoplastic response of functionally graded cemented carbidesdue to thermal loading
- Effect of aggregation intervalon vehicular traffic flow heteroscedasticity
- Application of neural network merging model in dam deformation analysis
- Mechanical analysis of transmission lines based on linear sliding cable element
- Improvement of pump-probe optical measurement technique using double moving stages
- Improvement of pump-probe optical measurement technique using double moving stages
