Optimal decision thresholdfor soft decision cooperative spectrum sensing
Sun Dafei Song Tiecheng Wu Ming Hu Jing Guo Jie Gu Bin
(1National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)(2College of Science, Nanjing University of Technology, Nanjing 210009, China)
The inflexible and fixed spectrum allocation in conventional wireless networks has been shown to encourage under-utilization of the spectrum. The cognitive radio (CR) has emerged as a promising technology to solve this problem through opportunistic access of the spectrum by unlicensed CR users, if non-harmful interference to the licensed primary user (PU) is guaranteed[1]. To ensure that the PUs are sufficiently protected against interference from the CR users, CR users should periodically perform spectrum sensing to obtain reliable results of the PUs’ activities[1-2].
Generally, spectrum sensing strategies are categorized into four basic kinds: energy detection, coherent detection, cyclostationary feature detection and eigenvalue-based detection. Due to its simplicity and efficiency, energy detection is recognized as a preferred scheme for practical implementation. To enhance the overall sensing accuracy, cooperation between multiple users is also suggested. Cooperation among CR users is usually cooperated by a fusion center (FC) through two types of fusion rules: hard decision fusion rules[3-4]and soft decision fusion rules[5-6]. In this paper, soft decision fusion rules are investigated, in which accurate energy values observed by different CR users are combined to make a satisfactory decision.
Generally, the performance of spectrum sensing depends greatly on the setting of the decision threshold. Threshold selection can be viewed as an optimization problem. Some research work has been done for this problem based on different objectives in Refs. [7-10]. In the Neyman-Pearson framework, the decision threshold is determined by a given target false alarm probability[4,6]. However, detectors under this scheme cannot achieve the minimum total error probability. In Ref. [7], based on the minimum total error rate criterion, the authors discussed the optimal decision threshold for hard decision cooperative spectrum sensing and the optimal decision threshold can be evaluated numerically. The main contribution of this paper is the derivation of a closed-form expression of the optimal decision threshold for soft decision cooperative spectrum sensing, which is based on the minimum total error probability criterion. The impact of different sensing parameters on the optimal decision threshold value is analyzed.
1 System Model
In this section we investigate cooperative spectrum sensing in a centralized CR network which consists of a FC and several CR users. Within the cognitive radio network, each CR user sends its sensing data to the FC periodically through common control channel. Then the FC combines the sensing data from different CR users and makes a decision on the presence or absence of the PU. For simplicity, we assume that the sensing data are sent from the CR user to the FC without any communication channel loss.
Here we consider a CR network withKCR users. Suppose thatNsamples are utilized for energy detection at each CR user. The spectrum sensing problem at thek-th CR user can be modeled as a binary hypothesis test problem, which is given by
wheres(n) denotes the primary signal;wk(n) denotes the additive white Gaussian noise (AWGN); andhkdenotes the channel gain between the PU and thek-th CR user. The channel gain is assumed to be constant during each sensing period. H0and H1denote the hypotheses corresponding to the absence and presence of the primary signal, respectively.
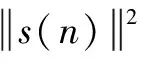
The energy detector measures the primary signal energy within a specified duration. Each CR user calculates a summary statisticYkover a detection interval ofNsamples, which is denoted as
(2)
Then cooperation diversity of multiple CR users is carried out in order to achieve better spectrum sensing performance.
We first consider local spectrum sensing at the individual CR user. The test statistic of thek-th CR user using energy detection is given by Eq.(2). For simplicity, assuming thatNis large enough, local test statisticYkapproximates the Gaussian distribution according to the central limit theorem, i.e.,
(3)
where N(μ,σ2) denotes the Gaussian distribution with the mean valueμand varianceσ2.
We setλkas the local decision threshold for thek-th CR user; the local false alarm probabilityPf,kand the detection probabilityPd,kcan be defined as

(4)
(5)
whereQ(·) denotes the complementary distribution function of the standard Gaussian. Based on the above definitions in Eqs.(4) and (5), the local missed probabilityPm,kcan be defined as
Pm,k=Pr(Yk<λk|H1)=1-Pd,k
(6)
2 Soft Combination
Cooperation among CR users is usually cooperated by a FC through two types of fusion rules: hard decision fusion rules and soft decision fusion rules. When hard decision fusion rules are used, CR users exchange only one bit of information regarding whether their observed energy value is above a certain threshold or not. In this paper, soft decision fusion rules are investigated in which accurate energy values observed by different CR users are combined to make a better decision. It is demonstrated that soft combination schemes have significant performance improvement over conventional hard combination[5].
For soft combination schemes, sensing data from different CR users is linearly combined with weight coefficients and decisions based on the weighted summation. To allow multiple CR users to collaborate, we transmit the test statistic {Yk} directly to the FC through the common control channel. Once the FC receives {Yk}, the global test statisticycis linearly calculated as[6]
(7)
wherewkdenotes the weight coefficient corresponding to thek-th CR user. The combining weight for the particular user represents its contribution to the global decision. For example, if a CR generates a high SNR signal which may lead to a correct detection on its own, it should be assigned by a larger weight coefficient. For those CR users which experience deep fading or shadowing, their weights should be decreased in order to reduce their negative contribution to the FC.
Assuming that {Yk} and {wk} are independent for differentk, then, according to Eq.(7),ycis under the Gaussian distribution. Then the global test statistic has means and variances which are given by
(8)
whereE[·] and var[·] denote the statistical expectation and variance, respectively.
The global test statistic is compared with a global decision thresholdλin order to make a global detection result. Ifyc>λ, the FC decides hypothesis H1is true; otherwise, the frequency band of interest is assumed not to be used by the PU, so the FC decides hypothesis H0is true.
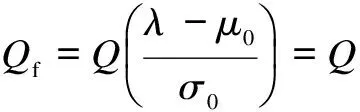
(9)

(10)
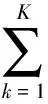
(11)
3 Optimal Decision Threshold Analysis
The essential problem of energy detector design is to determine the decision threshold in order to achieve ideal detection performance. Suppose that we choose a lower decision threshold, so that we will have a higher false alarm probability. On the contrary, if we choose a higher decision threshold, a larger missed detection probability will be achieved. Therefore, there exists a fundamental tradeoff between the probability of false alarm and the probability of missed detection.
Considering the tradeoff between the two error probability, we can know that minimizing the total error probability of spectrum sensing is significant for achieving the better performance of CR systems. For a given frequency band of interest, we defineP(H1) as the probability for which the primary user is present, andP(H0) as the probability for which the primary user is absent. Obviously, we can obtainP(H0)+P(H1)=1. The total error probabilityPeis defined as
Pe=αQf+βQm
(12)
whereα=P(H0) andβ=P(H1). We assume that the prior probabilityαis known for all the CR users based on long-term spectrum measurement. By minimizing the total error probability criterion,QfandQmare weighted and simplified as a measurement of the total error probability. For a special case in whichα=β, the total error probability is calculated as
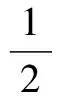
(13)
SubstitutingQfin Eq.(9) andQmin Eq.(11) into Eq.(12), the total error probability is given by
(14)
Therefore, our core goal is to determine the optimal decision threshold which can minimize the total error probability.
Proposition1If the decision thresholdλ∈(1,1+η), then both the false alarm probabilityQfand the missed detection probabilityQmare less than 0.5. Furthermore, letNapproach infinity, the false alarm probabilityQf→0, and the missed detection probabilityQm→0.
ProofIf the decision thresholdλ∈(1,1+η), then
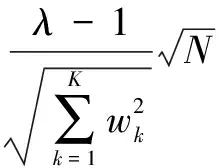
(15)
From Eqs.(9) and (10), according to the monotonicity of theQfunction, the detector performance can be derived as

(16)

(17)
Therefore, we can also have
Qm=1-Qd<0.5
(18)
Furthermore, whenNapproaches infinity, we can obtain
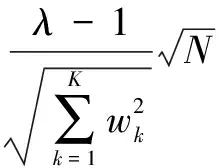
(19)
Thus, we can also see thatQf→0, andQm→0 whenNapproaches infinity.
In the field of spectrum sensing, a detection probability of 90% and a false alarm probability of 10% are regarded as the target requirements for all the sensing algorithms[4]. From Proposition 1, it follows that the constraintsQd>0.5 andQm<0.5 are equivalent to 1<λ<1+η.
Proposition2The total error probabilityPeis a convex function of the decision thresholdλ, when 1<λ<1+η.
ProofAccording to Eq.(14), differentiatingPewith respect toλgives
(20)
Then, the second-order derivative ofPewith respect toλis given by
(21)
If 1<λ<1+η, we can see thatλ-1>0, andλ-(1+η)<0. Then the second-order derivative ofPeis greater than 0, that is

(22)
Thus, the total error probabilityPeis convex inλwhen 1<λ<1+η.
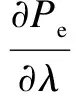
(23)
Solvingλby Eq.(23), the optimal decision threshold is taken to be the largest root. Hence, the optimal decision threshold can be determined by
(24)
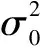
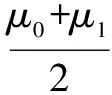
(25)
4 Simulation Results
In this section, simulation results are given to illustrate the impact of system parameters on the optimal threshold value for soft decision cooperative spectrum sensing. Under the Rayleigh fading environment, it is reasonable to assume that we have independent and identically distributed (i.i.d.) Rayleigh fading with the instantaneous SNRsγ1,γ2,…,γKbeing i.i.d. exponentially distributed random variables with the meanγ(i.e., the average SNR). The simulation results are obtained from 104realizations for the given constant channel gains.
First, we present the optimal decision threshold for different average SNRs when the equal gain combining (EGC), the maximal ratio combining (MRC), and the modified deflection coefficient (MDC) schemes[6]are adopted. The weight coefficients of the three soft combination schemes can be given as
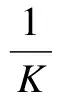
(26)

(27)
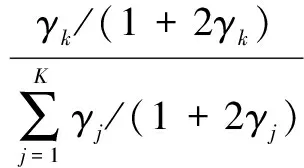
(28)
Here, we consider a system scenario with the number of CR usersK=4, the number of samplesN=100, and the prior probabilityα=0.5. Fig.1 describes the optimal decision threshold vs. the average SNRγfor three different soft combination schemes according to Eqs.(26), (27) and (28). Fig.1 shows that the optimal decision threshold is between 1 (lower bound) and 1+γ(upper bound). It can be also seen that the MRC and MDC schemes have almost the same optimal decision threshold in the low SNR region. Within the high SNR region, the optimal decision threshold for the MRC scheme is greater than that of the MDC scheme. Furthermore, in the low SNR region, the average SNRγ≈ηand then the optimal decision threshold for the EGC schemeλopt≈1+γ/2. In addition, Fig.2 depicts the minimum the total error probability for the corresponding three different soft combination schemes in Fig.1. From Fig.2, we can see that both the MRC and MDC schemes have nearly the same performance which outperforms that of the EGC scheme.
Secondly, we consider the impact of the prior probabilityαon the detector design of the optimal decision threshold. Here, we considerK=4,N=100, and the average
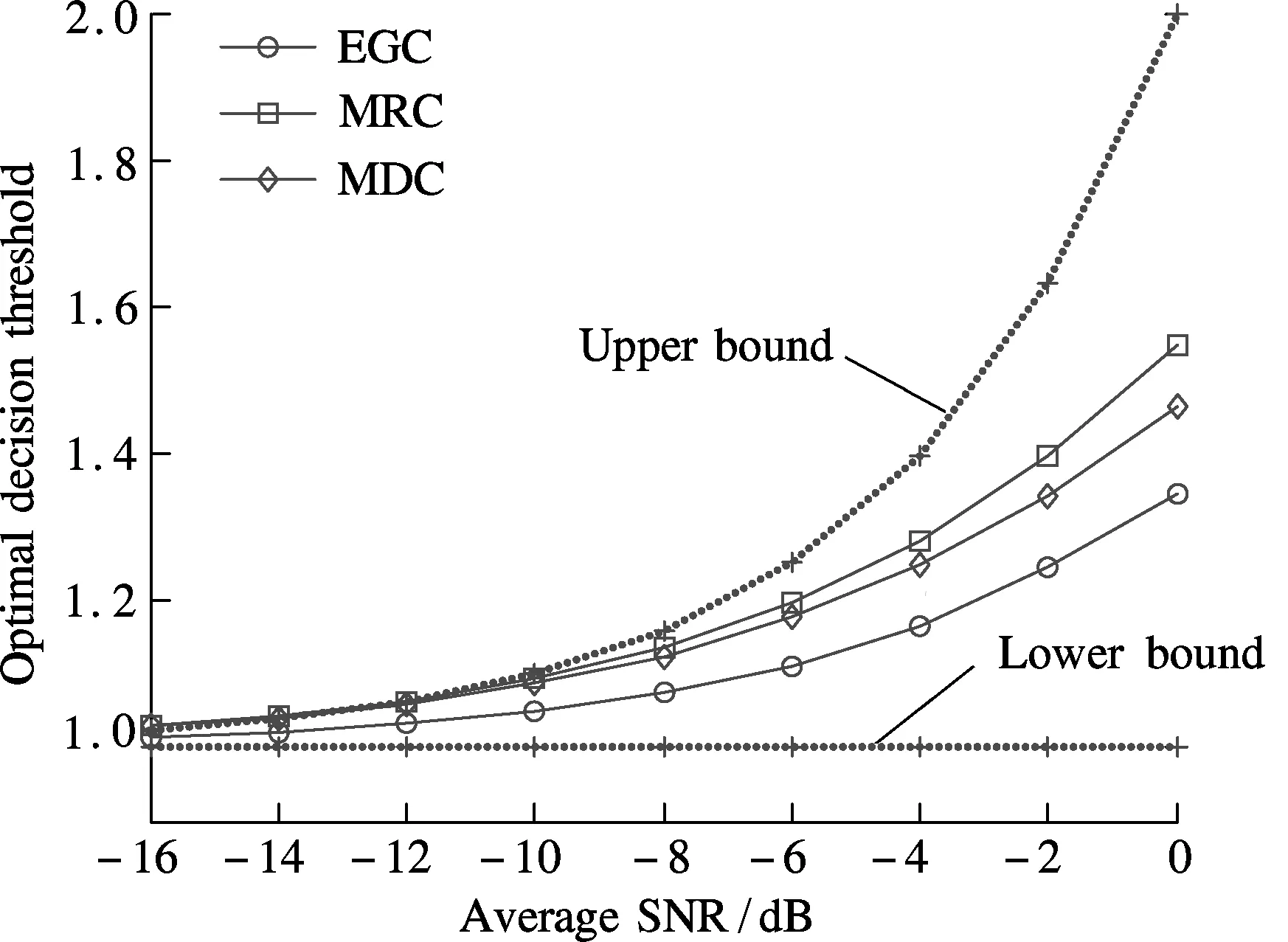
Fig.1 Optimal decision threshold vs. average SNR with three different soft combination schemes (K=4, N=100, and α=0.5)

Fig.2 Minimum total error probability vs. average SNR with three different soft combination schemes (K=4, N=100, and α=0.5)
SNRγ=-6 dB and -10 dB. Fig.3 illustrates the relationship between the optimal decision threshold value and the prior probabilityα. It can be seen from Fig.3 that the optimal decision threshold increases with the increase in the prior probabilityα, which means that the activity of the PU has effects on the design of the detector, which is reasonable. Since the PU is seldom present (i.e., the prior probabilityαis large), the optimal decision threshold value should be increased in order to obtain the target minimum the total error probability.
Thirdly, we consider the influence of the number of samples on the optimal decision threshold. We chooseK=4,α=0.5, and the average SNRγ=-6, -10 dB. Fig.4 describes the optimal decision threshold vs. the number of samples for three different soft combination schemes. It is verified that the number of samples has almost no influence on the optimal decision threshold. It can also be proved that the optimal threshold of the MRC scheme is greater than that of the MDC scheme. Furthermore, the MRC and MDC schemes have almost the same optimal decision threshold value with the average SNRγ=-10 dB.

Fig.3 Optimal decision threshold vs. prior probability with three different soft combination schemes (K=4, N=100, and the average SNR=-6, -10 dB)

Fig.4 Optimal decision threshold versus number of samples with three different soft combination schemes with K=4, α=0.5, and the average SNR=-6 dB, -10 dB
Finally, we analyze the impact of the number of CR users on the optimal decision threshold. Here we setN=100,α=0.5, and the average SNRγ=-6, -10 dB. Fig.5 plots the optimal decision threshold vs. the number of CR users for three different soft combination schemes. As the number of the CR user increases, the EGC scheme has almost the same optimal decision threshold, showing that the number of CR users has a weak influence on the optimal decision threshold for the EGC scheme. However, the optimal decision threshold values of MRC and MDC schemes increase as the number of the CR users increases, and the optimal decision thresholds for the two soft combination schemes approach a corresponding individual limit value while the number of CR users increases.
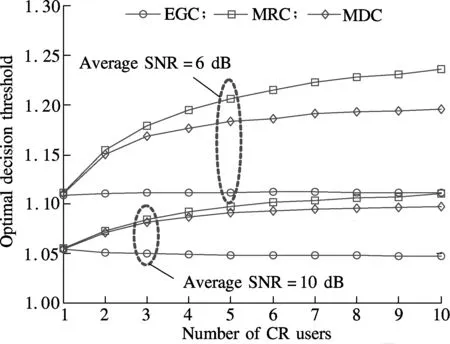
Fig.5 Optimal decision threshold vs. number of CR users with three different soft combination schemes (N=100, α=0.5, and the average SNR=-6, -10 dB)
5 Conclusion
In this paper, a closed-form expression of the optimal decision threshold is derived under the soft decision cooperative spectrum sensing scheme, including several parameters such as the weight coefficients, the prior probability of absence of the PU, the number of samples and the number of CR users. The impacts of these parameters on the optimal decision threshold are verified by detailed simulation results. It is demonstrated that the average SNR of soft combination schemes has a great effect on the value of the optimal decision threshold, whereas the number of samples has a weak influence on the value of the optimal threshold.
[1]Liang Y, Chen K, Li G, et al. Cognitive radio network-ing and communications: an overview [J].IEEETransVehTechnol, 2011,60(7): 3386-3407.
[2]Lu L, Zhou X, Onunkwo U, et al. Ten years of research in spectrum sensing and sharing in cognitive radio [J].EURASIPJWirelessCommunNetw, 2012,28(1): 1-16.
[3]Ghasemi A, Sousa E. Collaborative spectrum sensing for opportunistic access in fading environments [C]//ProcIEEEIntSymponNewFrontiersinDynamicSpectrumAccessNetworks. Baltimore, USA, 2005: 131-136.
[4]Liang Y, Zeng Y, Peh E, et al. Sensing-throughput tradeoff for cognitive radio networks [J].IEEETransWirelessCommun, 2008,7(4): 1326-1337.
[5]Ma J, Zhao G, Li G. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks [J].IEEETransWirelessCommun, 2008,7(11): 4502-4507.
[6]Quan Z, Cui S, Sayed A. Optimal linear cooperation for spectrum sensing in cognitive radio networks [J].IEEEJSelTopicsSignalProcess, 2008,2(1): 28-40.
[7]Zhang W, Mallik R, Letaief K. Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks [J].IEEETransWirelessCommun, 2009,8(12): 5761-5766.
[8]Fan R, Jiang H, Guo Q, et al. Joint optimal cooperative sensing and resource allocation in multichannel cognitive radio networks [J].IEEETransVehTechnol, 2011,60(2): 722-729.
[9]Luo L, Roy S. Efficient spectrum sensing for cognitive radio networks via joint optimization of sensing threshold and duration [J].IEEETransCommun, 2012,60(10): 2851-2860.
[10]Gong S, Wang P, Huang J. Robust performance of spectrum sensing in cognitive radio networks [J].IEEETransWirelessCommun, 2013,12(5): 2217-2227.
 Journal of Southeast University(English Edition)2013年4期
Journal of Southeast University(English Edition)2013年4期
- Journal of Southeast University(English Edition)的其它文章
- Elastoplastic response of functionally graded cemented carbidesdue to thermal loading
- Effect of aggregation intervalon vehicular traffic flow heteroscedasticity
- Application of neural network merging model in dam deformation analysis
- Mechanical analysis of transmission lines based on linear sliding cable element
- Improvement of pump-probe optical measurement technique using double moving stages
- Improvement of pump-probe optical measurement technique using double moving stages
