H.264中一种基于搜索范围自适应调整的运动估计算法

刘英哲 王进祥

(哈尔滨工业大学微电子中心 哈尔滨 150001)

1 引言

H.264视频编码标准中，运动估计被用来消除视频序列的时间冗余。在带来较高压缩质量的同时，运动估计也导致了编码算法复杂、运算量大，给实时视频通信带来困难。尤其是当搜索范围的大小随着视频序列分辨率的提高而不断增加时，从存储器中读取参考像素时对存储带宽的要求逐渐成为实时编码器的主要瓶颈。研究表明通常情况下运动估计单元占据了整个编码系统50%以上的运算量，而对于存储器的读写操作占用则达90%左右[1,2]。因此在保证压缩效率和编码质量的前提下，降低运动估计单元的复杂度是提高整个编码系统效率，满足实时视频通信要求的关键所在。

降低运动估计复杂度的主要方法有搜索范围(SR)调整算法和模板匹配算法。模板匹配算法在搜索窗(SW)内通过使用模板进行匹配来减少计算量。相比于模板匹配算法，SR调整算法在减少运算量的同时，由于能够预先判决搜索区间的大小，还能够有效地降低运动估计时对参考帧存储器的访问次数。文献[3]对典型测试序列仿真，得出不同测试序列搜索区域大小的统计分布情况，以及搜索区域大小对视频压缩率和质量的影响。由于其是早期对SR的研究工作，所以仅仅给出了不同分辨率视频序列应选择的搜索范围大小。文献[4,5]使用最大似然估计建立运动矢量差值(MVD)的概率密度函数，根据预先给定的命中率计算最佳搜索范围。但是该方法中的积分运算和似然估计导致算法非常繁琐。文献[6]将视频序列划分为静止的背景区域和运动的前景区域，对于不同的区域给予不同的 SR判断方法。文献[7]利用视频序列的空间相关性，将当前编码块的SR定义为相邻块最大匹配误差的函数。文献[6,7]的算法在选取 SR时都是根据一定的准则选取最坏情况下的SR值，因此导致其算法效率不高。文献[8,9]从多个方面对运动估计进行了优化，其中针对 SR选择方面，将编码块的运动剧烈程度按照预测运动矢量(PMV)的大小划分为静止、平缓和剧烈，相应地选择3×3, 7×7和9×9大小的搜索范围。文献[10]根据预先设定的阈值和3种固定大小搜索区域，为当前编码块选择SR。然而文献[8-10]由于仅仅采用了几种固定的搜索范围和阈值，导致算法自适应性较差，无法满足视频序列多样性的特点，并且复杂度的降低也很有限。文献[11]阐明了16×16块和8×8块的SR和其它类型分割块SR大小具有一定的相关性，因而可以直接将16×16块和8×8块的SR作为其它尺寸块的SR。但是由于其不加区分地直接使用顶层尺寸块SR作为底层编码块的SR，因此该算法对复杂度的降低也不高。文献[12]通过MVD的概率密度函数和相邻块运动矢量(MV)分布的对应关系计算当前编码块的搜索区域。文献[13]分析了宏块压缩比率和 SR大小的对应关系，通过对压缩比率较小的宏块选取较小 SR的方法，减少运动估计时对存储器的访问次数。文献[14]定义了基于单比特变换SR的线性模型来计算编码块的SR。由于该算法是以单比特图像(one-bit image)为基础，其在较大幅度降低复杂度的同时，也给编码质量和输出码率带来了较大的损失。文献[15]针对可分级视频编码(SVC)提出了一种基于内容自适应的运动估计算法，在设定搜索区间大小时，根据编码块所在区域的运动剧烈程度相应地从预先设定的3种搜索区间中进行选取。

综上所述，使用以上算法能够减少搜索区间的大小，降低系统的复杂度，但是其效率还有待于进一步提高。首先SR和PMV的相关性没有得到有效利用，运动估计是以 PMV为中心进行搜索的，因此即使运动较为剧烈的编码块，对于准确的 PMV应该对应较小的SR；其次以上算法仅仅考虑了编码块的运动幅度而忽略了编码块运动的方向特性。基于此，本文提出了一种新的 SR调整算法，在保证压缩效率和编码质量的前提下，能够进一步降低编码的复杂度。本文算法首先利用当前块在 PMV点的绝对误差和(SAD)以及相邻已编码块的信息，判断 PMV的预测准确程度，动态地调整搜索范围的大小；然后根据已编码块的运动矢量场，判断编码块所在区域是否具有一致的运动方向特性，进一步减少计算量。

2 本文提出的算法

2.1 算法的基本思想

动态 SR的基本思想是，包含运动剧烈物体的编码块对应较大SR，而对于运动平缓的物体采用较小SR。按照该方法进行判断时存在两个问题，首先物体运动特性具有多样性，文献[8-10]采用阈值的方法对编码块的运动程度进行分类，但是简单的阈值设定无法满足自然场景中物体运动的丰富特性；其次H.264编码标准中，运动估计的初始搜索点是通过相邻已编码块的MV预测得到，因此搜索范围更大程度是由PMV的位置决定的。图1中，PMV作为运动估计的起始搜索点，由已编码块A,B和C的运动矢量中值预测得到，X为当前编码块，MV为块X经运动估计得到的运动矢量，灰色区域为实际有效搜索范围。由图1可见，当运动矢量预测值PMV较为精确时，即PMV距离MV较近时，无需搜索过多的区域，就能得到编码块X的MV；反之如果PMV距离MV较远，则需要在较大的SR内搜索。

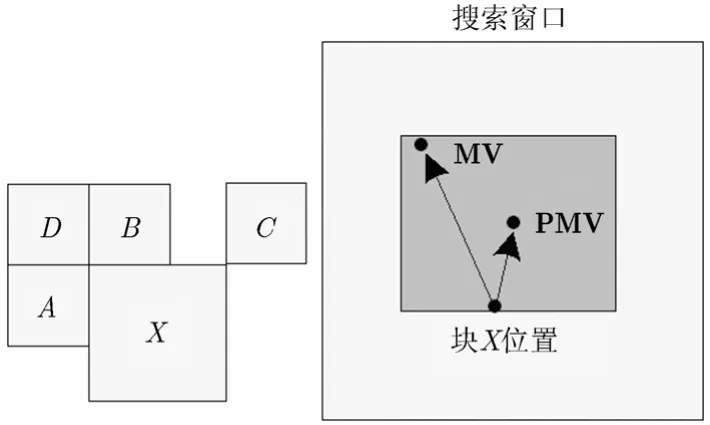
图1 MV和PMV的关系

模板匹配方法中认为代价函数值随着搜索点逐渐接近MV而单调减少，因此可以使用模板沿着代价函数递减的方向进行搜索。基于此思想，使用编码块X在PMV点对应的绝对误差和(SAD)来衡量PMV的预测准确程度，即 SAD越小 PMV距离MV越近，对应的SAD表示为

式(1)中，Curr(i,j)为当前帧中(i,j)点的像素值，PmvX和PmvY分别为预测运动矢量PMV的水平和垂直分量，W和H分别为当前编码块的长度和宽度，refn(i+PmvX,j+PmvY)为参考帧n中(i+PmvX,j+PmvY)点的像素值。已编码块A,B,C和D各自MV点的SAD分别标记为Sada, Sadb, Sadc和Sadd，这4个SAD值分别代表了这4个块运动估计得到的最佳匹配点的SAD值。根据视频序列的空间相关性，可以使用这4个相邻块的SAD值衡量编码块X预测运动矢量的准确度，即PMV的准确度和Sadpmv接近这4个SAD的程度具有相关性。将Sadpmv与Sada,Sadb, Sadc和Sadd的差值构成集合：

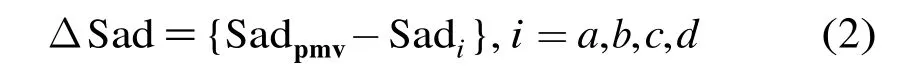
按照下面条件判断：

条件 1 如果ΔSad中有元素小于等于 0，即Sadpmv小于某一相邻块MV点的SAD值，此时可以确定块X的PMV较为接近MV，因此应该设置较小的搜索范围，SR等于

式(3)中SRa, SRb, SRc和SRd分别为块A,B,C和D运动估计后得到的SR。

条件2 当集合ΔSad中所有元素都大于0，且Sadpmv>3max(Sada,Sadb,Sadc,Sadd)，即 Sadpmv大于3倍的相邻块最大SAD值，表明PMV距离MV较远。此时，为了保证编码的质量，应该选择较大的SR值：

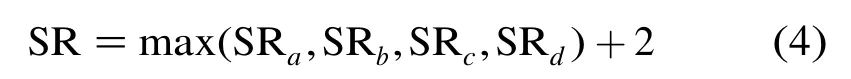
条件3 当条件1和条件2都不满足时，表明PMV的准确程度一般。从集合ΔSad中选取两个最小的元素，即4个SAD值中和Sadpmv最接近的两个，其对应的块分别记做b1和b2，此时SR值设定为

按照式(3)~式(5)确定 SR的大小后，根据 SR将相应的参考像素读入到搜索窗中，但是逐一对SR内的所有点进行匹配计算是没有必要的。这是因为当前 SR的确定仅仅考虑了物体的运动幅度，而忽略了物体的运动方向。图2为测试序列Stefan_cif第12帧部分运动矢量场。

从图2中可见，除物体边界外，相邻区域的MV具有很强的方向相关性。例如，整个上部分区域内的MV以右上方向为主，而右下区域内物体的运动方向接近水平。因此如果能够确定编码块X所在区域的大致运动方向，就可以仅仅计算 SR内符合运动方向的匹配点，对于运动方向外的其它区域不进行计算。相邻块A,B和C，以及前一帧中的共同位置(co-located)块E的MV用来判断块X所在区域的运动方向，如图3所示，图中MVA,MVB,MVC和MVE分别代表这4个块的运动矢量。

图2 测试序列Stefan_cif 第12帧部分运动矢量场

图3 相邻编码块和编码区域的运动方向

如果这4个块的运动矢量方向基本一致，表明编码块X所在区域内的物体具有较为明显的运动方向一致特性，块X遵循该区域的运动方向的可能性较大；相反如果这4个块的运动方向差异较大，则表明区域内包含的物体运动方向一致性不明显。具体算法为： 用MV和x轴的夹角θ(-π＜θ≤π)表示运动矢量的方向，计算A,B,C和E块θ的均值μ，将4个块的θ值的相关性定义为CR：

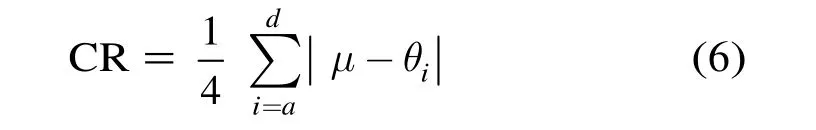
CR代表了这4个θ的相关程度，当CR较小时表明4个已编码块的运动方向差异不大。具体判断方法如下：

条件1 如果CR≤TH(TH为判断阈值，通过仿真试验设置为0.15)，表明该区域内4个块的运动方向比较接近，区域包含的物体运动方向一致性明显，编码块X的MV应该遵循该区域的运动方向，块X的运动方向θx应该满足条件：

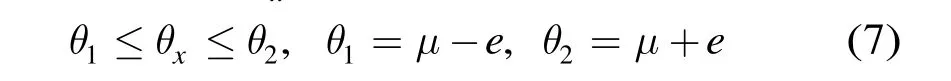
e设置为0.4，由仿真试验统计得到。图3中的灰色区域为根据式(7)确定的匹配计算区间。

条件2 如果CR＞TH则表明这4个已编码块的运动方向差异较大，块X所在区域内物体运动方向一致性不明显。为保证编码的质量，不限制搜索方向。

2.2 算法的基本流程

图4为本文算法的流程图，算法的具体步骤说明如下：

步骤1 如果编码块的空间相邻块A,B,C和D都可用，转步骤 2；否则直接使用编码器配置文件设定的搜索范围进行运动估计。

步骤2 计算Sadpmv与A,B,C和D块MV点SAD的差值，构成集合ΔSad，并按照下面的条件进行判断：

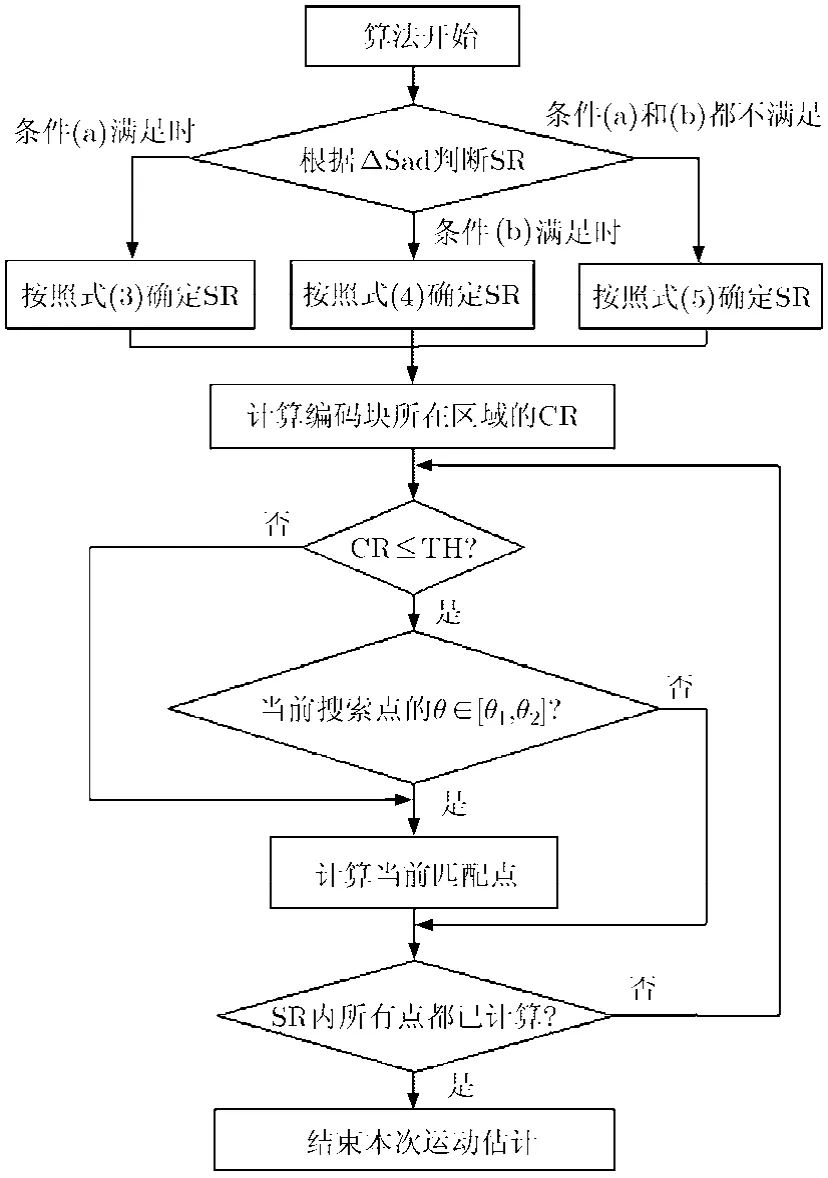
图4 本文算法的流程图

条件(a)如果 min(ΔSad)≤0，按照式(3)设定SR，转步骤3。

条件(b)如果 Sadpmv>3max(Sada, Sadb, Sadc,Sadd)，按照式(4)设定SR，转步骤3。

条件(c)如果条件(a)和条件(b)都不满足，则按照式(5)设定SR，转步骤3。

步骤3 使用已编码块A,B,C和E的运动方向θ计算编码块所在区域的CR，转步骤4。

步骤4 判断编码块所在区域的运动特性，如果CR＞TH表明该区域内物体运动不具有一致性，转步骤6；否则转步骤5。

步骤5 如果当前搜索点的运动方向θ∈[θ1,θ2]，表明当前搜索点运动方向和编码块所在区域运动方向一致，转步骤6；否则转步骤7。

步骤6 对当前搜索点进行匹配计算，转步骤7。

步骤7 如果SR内所有的搜索点都已经计算，结束本次运动估计；否则转步骤4判断下一搜索点。

3 仿真结果分析与对比

将本文算法集成到 H.264软件编码器 JM16.2中，选取不同尺寸的测试序列进行仿真对比。编码器配置文件设置如下：编码帧数量为100; CIF尺寸(352×288)序列的搜索范围设为 16, 4CIF尺寸(704×576)序列的搜索范围设为 32, HD 尺寸(1920×1080)序列的搜索范围设为 64；编码结构设置为IPPP…；量化参数为22, 28, 34 和 40；参考帧数量设为 1；率失真优化和哈达码变换设置为开；运动估计分别设置为全搜索(FS)和UMHexagon。

表1将本文算法与JM16.2和文献[11]的编码结果进行了比较。其中ΔPSNR代表PSNR相对变化情况，单位为dB, ΔPSNR为正时代表编码质量的上升，反之代表质量的下降；BR代表码率百分比变化情况，正值代表压缩码率增加，负值代表压缩码率降低；ΔMET是运动估计耗时相对变化情况。表1中ΔPSNR, ΔBR和ΔMET是QP分别为22,28, 34和 40时编码对比结果的平均值。从表1中可以看出，对于12个标准测试序列，本文算法相对于全搜索算法和UMHexagon算法平均节约了91%和18%左右的运动估计时间，并且本文的算法是以搜索范围自适应调整技术为基础的，在减少运算量的同时，还能够降低运动估计时对参考帧存储器的访问。尤其是对于HD尺寸的测试序列，本文算法较FS算法平均节约了95%左右的运动估计时间。这是由于按照固定范围设置搜索区域时，搜索范围的大小随着图像的分辨率提高而增加，而本文的算法能够自适应地调整搜索范围的大小。和文献[11]相对比时，本文算法在取得了和文献[11]基本相同的PSNR和码率的前提下，能够平均节约21%的运动估计时间。

表 2为本文算法和文献[4]算法编码性能的比较，在和文献[4]的算法对比时，选取了和文献[4]相同的测试序列，并采用文献[4]中定义的 CPX(Computational Complexity)对编码结果进行统计比较。CPX代表了SR自适应调整算法的搜索点数量和JM源码搜索点数量的比值，具体定义为

式(8)中SRJM为 JM配置文件中设置的搜索范围；SPNji为使用自适应调整算法时第j个编码帧中第i个宏块的平均搜索点数；M和N分别为编码帧总数和每帧包含的宏块数量。从表2的数据可以得到，本文较文献[4]的算法能够平均节约 1%的码率，而CPX大约为文献[4]的一半，证明了本文算法的优越性。

为了直观比较算法的率失真性能，图5给出了Akiyo_cif和 Stefan_cif两个典型测试序列的率失真曲线图。其中 Akiyo_cif中物体运动平缓，并且包含大部分的静止背景，是运动平缓测试序列的典型代表。Stefan_cif中物体运动剧烈不规则，是运动剧烈序列的典型代表。本文算法在节省运算时间大大优于文献[4]和文献[11]的前提下，从图 5中可见，本文算法和文献[11]算法的率失真曲线基本是重合的，说明本文算法和文献[11]具有基本相同的率失真性能；而对比于文献[4]的率失真曲线，本文算法具有较好的率失真性能。

表2 本文算法和文献[4]编码性能比较

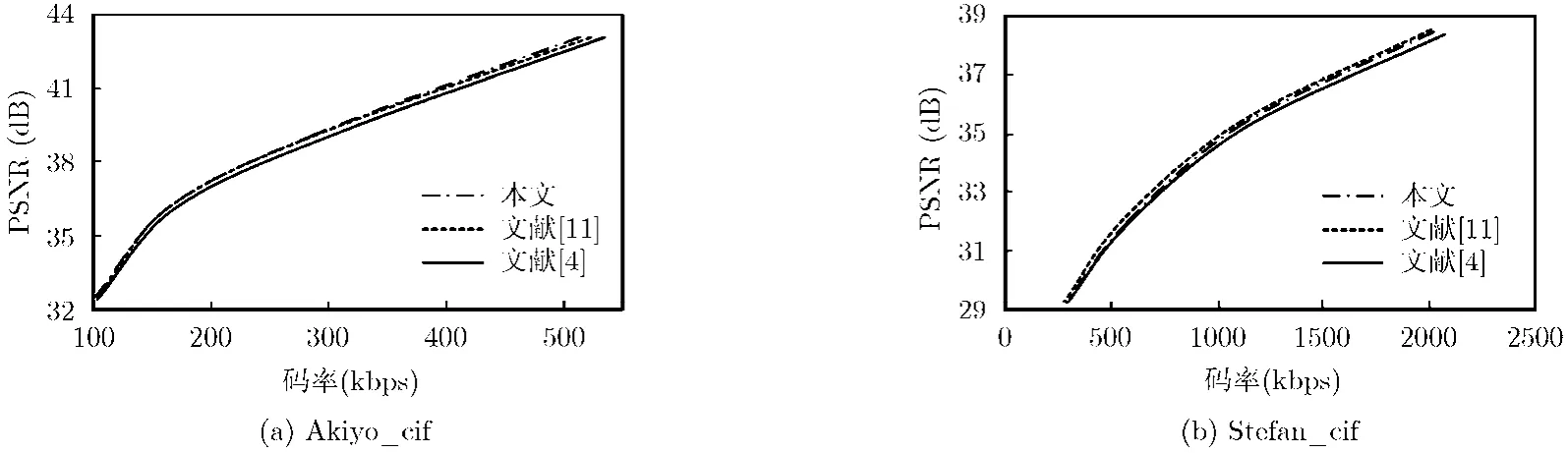
图5 率失真曲线比较

4 结束语

为了降低H.264中运动估计单元的复杂度，本文提出了一种搜索区域自适应调整算法。算法首先利用已编码块的信息，判断当前编码块 PMV的准确程度，决定搜索区间的大小，减少读入的参考像素，然后根据编码区域的运动方向特性，减少需要计算的匹配点数量。仿真数据表明：该算法平均节省运动估计时间达 91%，有利于实时应用；PSNR平均下降约0.050 dB，不会影响主观视觉效果；同时码率平均增加 0.66%左右，保证了压缩效率。因此本文算法在保证编码性能的前提下，能够有效地降低H.264运动估计过程的复杂度，且本文算法相比于大多数算法具有一定的优势。研究本文算法对应运动估计单元的超大规模集成电路(VLSI)结构是下一步工作的重点。

[1] He Z, Liang Y, Chen L,et al.. Power-rate-distortion analysis for wireless video communication under energy constraints[J].IEEE Transactions on Circuits and Systems for Video Technology, 2005, 15(5): 645-658.

[2] Denolf K, Blanch C, Lafruit G,et al.. Initial memory complexity analysis of the AVC codec[C]. IEEE Workshop on Signal Processing Systems, San Diego, America, 2002:222-227.

[3] Gonzales C A, Yeo H, and Kuo C J. Requirements for motion-estimation search range in MPEG-2 coded video[J].IBM Journal of Research and Development, 1999, 43(4):453-470.

[4] Ko Yun-ho, Kang Hyun-soo, and Lee Si-woong. Adaptive search range motion estimation using neighboring motion vector differences[J].IEEE Transactions on Consumer Electronics, 2011, 57(2): 726-730.

[5] Kang Hyun-soo, Lee Si-woong, and Hosseini H G. Probability constrained search range determination for fast motion estimation[J].JournaloftheElectronicsand Telecommunications Research Institute, 2012, 34(3): 369-378.

[6] Kim Ilseung and Kim Joohyeok. Low-complexity block-based motion estimation algorithm using adaptive search range adjustment[J].OpticalEngineering,2012, 51(6):067010-1-067010-9.

[7] Lee Sangkeun. Fast motion estimation based on search range adjustment and matching point decimation[J].IET Image Processing, 2010, 4(1): 1-10.

[8] Ismail Y, Elgamel M A, and Bayoumi M A. Fast variable padding motion estimation using smart zero motion prejudgment technique for pixel and frequency domains[J].IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(5): 609-626.

[9] Ismail Y, Mcneely J B, Shaaban M,et al.. Fast motion estimation system using dynamic models for H.264/AVC video coding[J].IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(1): 28-42.

[10] Lee Si-woong, Park Seong-mo, and Kang Hyun-soo. Fast motion estimation with adaptive search range adjustment[J].Optical Engineering, 2007, 64(4): 040504-1-040504-3.

[11] Lee Sun-young, Choi K, and Jang E S. Adaptive search range adjustment scheme for fast motion estimation in H.264/AVC[J].OpticalEngineering, 2011, 50(6):067402-1-067402-6.

[12] Lou Chung-cheng, Lee Szu-wei, and Jay Kuo C C. Adaptive motion search range prediction for video encoding[J].IEEE Transactions on Circuits and Systems for Video Technology,2010, 20(12): 1903-1908.

[13] Jung Jongpil, Kim Jaemoon, and Kyung Chong-min. A dynamic search range algorithm for stabilized reduction of memory traffic in video encoder[J].IEEE Transactions on Circuits and Systems for Video Technology, 2010, 20(7):1041-1046.

[14] Urhan O. Constrained one-bit transform based fast block motion estimation using adaptive search range[J].IEEE Transactions on Consumer Electronics, 2010, 56(3):1868-1871.

[15] She Li-quan and Zhang Zhao-yang. Content-adaptive motion estimation algorithm for coarse-grain SVC[J].IEEE Transactions on Image Processing, 2012, 21(5): 2582-2591.