非齐次发展型p-Laplace方程正解的爆破性和存在性
孙 鹏,孔德建,李建军,高文杰
(1.吉林大学数学学院,吉林长春 130012;2.辽宁工程技术大学理学院,辽宁鞍山 130000)
非齐次发展型p-Laplace方程正解的爆破性和存在性
孙 鹏1,孔德建1,李建军2,高文杰1
(1.吉林大学数学学院,吉林长春 130012;2.辽宁工程技术大学理学院,辽宁鞍山 130000)
考虑了非齐次发展型p-Laplacian方程带有非负初值的Cauchy问题∂tudiv(|▽um|p-2▽um)=uq+w(x),这里p>1,q>max{1,m(p-1)},而且w(x)≢0∈R Rn是一个非负连续函数.证明了当2n/(n+1)<p<n时,qc=mn(p-1)/(n-p)是临界指标,即如果q≤qc,则该问题的所有正解在有限时刻内爆破;而当q>qc时,对于满足某些条件的w(x)以及某些初值,方程存在全局正解.并且证明了当n≤p时,该问题的正解在有限时刻内均爆破.
非齐次发展型p-Laplacian方程;临界指标;爆破;全局存在
1 预备知识
在本文中,我们主要研究如下的非齐次发展型p-Laplace的Cauchy问题正解的全局存在性和爆破性:
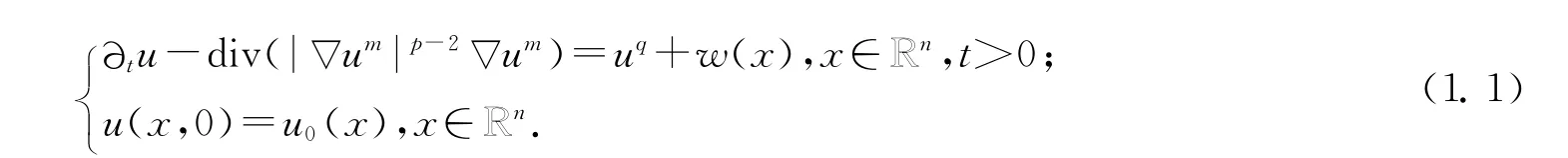
这里p>1,q>max{1,m(p-1)},m≥1,并且w(x)≢0和u0(x)均为R Rn上的非负函数.
这类方程来源于自然界中广泛存在的扩散现象.在诸如生物化学以及生物种群的动态等诸多领域的物理问题,都可以归结为这类数学模型.
[1]中,H.Fujita研究了半线性热传导方程的Cauchy问题

这里p>1,并得到如下结果:
(a)若p<1+2/n,则所有非平凡解u(x,t)在有限时刻爆破;
(b)若p>1+2/n且u0(x)≤δe-|x|2(0<δ≪1),则问题(1.2)存在一个全局解.
对于p=1+2/n的情况,文献[2-3]分别给出了n=1,2以及n≥1时,问题(1.2)不存在全局解u(x,t)满足‖u(·,t)‖∞<∞.文献[4]证明了,若p=1+2/n,则问题(1.2)当t>0,q∈[1,+∞)时,不存在满足‖u(·,t)‖q<∞的全局解u(x,t).我们称p c=1+2/n为问题(1.2)的临界指标,它对研究问题(1.2)解的性质具有重要意义.
在过去的几十年间,H.Fujita的结果在许多方面都得到了大量的推广.最近文献[5-13]将H.Fujita的结果推广到了非齐次方程的Cauchy问题.在这种问题中,临界指标和爆破点均与齐次方程有所不同.此时,问题的临界指标更多的与相应的椭圆问题的临界指标具有紧密的联系.
对于发展型p-Laplace方程的Cauchy问题,文献[12]讨论了齐次方程的情况,并得到了临界指标qc=p-1+p/n,证明了当p>2n/(n+1)时,如果max{1,p-1}<q<qc,则Cauchy问题没有全局解,而如果q>qc,并且初值u0(x)充分小,则Cauchy问题存在全局正解.文献[9]讨论了具有双重奇异性的抛物方程,并得到了相似的结果.
文献[14]讨论了发展型p-Laplace方程∂tu-div(|▽u|p-2▽u)=uq+w(x)带有非负初值的Cauchy问题,证明了当2n/(n+1)<p<n时,qc=(p-1)n/(n-p)为问题的临界指标,即如果q≤qc,则问题的正解在有限时刻爆破;而如果q>qc,则该方程对于某些w(x)的适当的初值存在全局正解.文献[14]还证明了当n≤p时,问题的正解在有限时刻均爆破.文献[15]讨论了一类拟线性退化抛物型方程组解的爆破性.
本文的主要目的是研究问题(1.1)正解的性质.当m(p-1)≥1时,方程具有退化性和奇异性,即如果m>1或p>2,则方程在u(x,t)=0或|▽u(x,t)|=0处具有退化点;如果0<m<1或1<p<2,则方程在u(x,t)=0或|▽u(x,t)|=0处具有奇异点.我们将证明qc=(p-1)nm/(n-p)是问题(1.1)的临界指标.确切地说,如果q<qc,则问题(1.1)的正解对于任何非负初值总是爆破的;如果q>qc,则对一些适当大的初始条件,问题(1.1)的解在有限时刻爆破,并且若初始条件适当小,则其解是全局存在的;而如果q=qc,则问题(1.1)的解总是在有限时刻爆破.
我们的主要结果如下:

2 解的先验估计



3 定理的证明





[参 考 文 献]
[1]FUJITA H.On the blowup of solutions of the Cauchy problem forut=Δu+u1+σ[J].J Fac Sci Univ Tokyo Sect,1966,13:109-124.
[2]HAYAKAWA K.On nonexistence of global solutions of some semilinear parabolic equations[J].Proc Japan Acad,1973,49:503-525.
[3]KOBAYASHI K,SIRAO T,TANAKA H.On the blowing up problem for semilinwar heat equations[J].Math Soc Japan,1977,29:407-424.
[4]WEISSLER F B.Existence and nonexistence of global solutions for a semilinear heat equations[J].Israel J Math,1981,38:29-40.
[5]BANDLE C,LEVINE H A,ZHANG Q S.Critical exponents of Fijita type for inhomogeneous parabolic equations and systems[J].J Math Anal Appl,2000,251:624-648.
[6]DENG K,LEVINE H A.The role of critical exponents in blow-up theorems:the sequel[J].J Math Anal Appl,2000,243:85-126.
[7]LEVINE H A.The role of critical exponents in blow-up theorems[J].SIAM Rev,1990,32:262-288.
[8]LIONS P L.The concentration-compactness principle in the calculus of variations,the limit case[J].Rev Mat Iberoamericana,1985(1)/(2):145-201/45-121.
[9]LIU X F,WANG M X.The critical exponent of doubly singular parabolic equations[J].J Math Anal Appl,2001,257:170-188.
[10]陆文端.微分方程中的变分方法[M].北京:科学出版社,2003:24-104.
[11]QI Y W.On the equationut=Δuα+uβ[J].Proc Roy Soc:Edinburgh Sect A,1933,123:373-390.
[12]ZHAO J N.On the Cauchy problem and initial traces for the evolutionp-Laplacian equations with srongly nonlinear sources[J].J Differential Equations,1995,121:329-383.
[13]ZHANG Q S.Blow-up results for nonlinear parabolic equations on manifolds[J].Duke Math J,1999,97:515-539.
[14]ZENG XIANZHONG.Blow-up results and global existence of positive solutions for the inhomogeneous evolutionp-Laplacian equations[J].Nonlinear Analysis,2007,66:1290-1301.
[15]魏英杰,邬娟.一类拟线性退化抛物型方程组解的存在性与爆破[J].吉林大学学报:理学版,2010,48(3):406-408.
[16]SERRIN J,ZOU H H.Cauchy-Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities[J].Acta Math,2002,189:79-142.
[17]YIN JINGXUE,LI JING,JIN CHUNHUA.Non-extinction and critical exponent for a polytropic filtration equation[J].Nonlinear Analysis,2009,71:347-357.
Blow-up and global existence of positive solutions for inhomogeneous evolutionp-Laplace equations
SUN Peng1,KONG De-jian1,LI Jian-jun2,GAO Wen-jie1
(1.Institute of Mathematics,Jilin University,Changchun 130012,China;2.College of Science,Liaoning Technical University,Anshan 130000,China)
This paper deals with the Cauchy problem of inhomogeneous evolutionp-Laplacian equations∂tu-div(|▽um|p-2▽um)=uq+w(x)with nonnegative initial data,wherep>1,q>max{1,m(p-1)},andw(x)≢0 is a nonnegative continuous function in R Rn.It is proved thatqc=mn(p-1)/(n-p)is a critical exponent provided that 2n/(n+1)<p<n,i.e.,ifq≤qc,then every positive solution blows up in finite time;whereas forq>qc,the equation possesses a global positive solution for somew(x)and some initial data.Meanwhile,it also proves that positive solutions blow up in finite time provided thatn≤p.
inhomogeneous evolutionp-Laplace equation;critical exponent;blow-up;global existence
O 175.26
110·34
A
1000-1832(2012)01-0001-09
2011-01-17
国家自然科学基金资助项目(10771085);吉林大学数学学院人才基地本科生科研项目(J1030101,J0630104,
J0730104).
孙鹏(1978—),男,博士,讲师,主要从事发展方程研究;高文杰(1956—),男,博士,教授,博士研究生导师,主要从事应用数学研究.
陶 理)

