渗透率模型研究进展

孙建孟，闫国亮

（中国石油大学地球科学与技术学院，山东青岛266555）

渗透率模型研究进展

孙建孟，闫国亮

（中国石油大学地球科学与技术学院，山东青岛266555）

讨论单重孔隙介质和双重孔隙介质渗透率模型的发展，分析渗透率建模面临的问题：建模理论研究缺乏，至今没有提出统一的模型，双重孔隙介质渗透率模型亟待发展。单重孔隙介质渗透率与孔隙度相关性较好，但仅有孔隙度不能建立精确的渗透率模型，还需考虑岩石结构和孔隙结构参数。双重孔隙介质渗透率可分为基质渗透率和裂缝渗透率2个方面研究，它们之间的耦合是渗透率建模重点考虑的问题。提出应用分形理论和成像测井有望提高双重孔隙介质渗透率模型的建模精度。渗透率建模发展方向是三维数字岩心技术和激发极化法的应用。

测井解释；岩石物理性质；渗透率模型；单重孔隙介质；双重孔隙介质；研究进展；数字岩心

0 引 言

绝对渗透率是指当只有单一流体在岩石孔隙中流动而与岩石没有物理化学作用时所求得的渗透率，它是一个表征流体在岩石内部流动难易程度的岩石物理参数。渗透率在油田开发中起着十分重要的作用，井的数量、井间距的确定和地面油管设施的设计，都离不开渗透率的准确获取。但是渗透率是一个难以直接通过测井方法获取的岩石物理参数，一般通过建立其他岩石物理参数与渗透率的物理模型，将测井方法可以直接测量的参数转换为渗透率。

渗透率不仅与孔隙度有关，还与孔隙结构、岩石结构及构造特征有明显的关系。对于单重孔隙介质，在孔隙度相同的条件下，一些结晶白云岩和颗粒灰岩要比由泥粒灰岩和泥岩组成的岩石的渗透率高很多［1］。对于双重孔隙介质，由于岩石有导通的微裂缝，虽然孔隙度变化不大，但渗透率会提高几个数量级［2］。因此，要进行可靠的渗透率预测，除孔隙度以外，还必须考虑其他参数，如孔隙形状、孔隙大小分布等。对于有裂缝的岩石，更要充分考虑裂缝参数，如裂缝密度、裂缝开度和裂缝倾角等。本文主要介绍不同孔隙特征岩石渗透率模型的研究现状，包括含有单重孔隙和双重孔隙的岩石。目前关于单重孔隙介质的渗透率模型研究比较成熟，而双重孔隙介质的渗透率模型研究尚不成熟。

1 渗透率模型研究现状

1.1 单重孔隙介质的渗透率模型

单重孔隙介质的孔隙空间主要由原生粒间孔隙组成，孔隙尺度在微米到亚微米量级，且孔隙尺寸变化范围相对较小，均质性较好。

最早对单重孔隙砂岩油藏的研究发现，渗透率的对数与孔隙度有线性关系［3］

式中，K为渗透率，mD＊＊非法定计量单位，1mD＝9.87×10－4μm2，下同；φ为孔隙度，%；a和b为经验常数。式（1）具有区域性，没有考虑孔隙结构变化的影响，不能满足复杂储层渗透率的精度要求。

对于均匀孔隙介质，Kozeny根据毛细管理论提出了一个公式［4］，后来Carman对这个公式进行了证明［5］，即Kozeny－Carman公式，简称KC公式。它是一个理论公式，常用形式为［6］

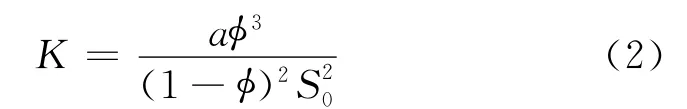
式中，S0为比表面积，m2／m3；a为经验常数。由于比表面积不同的定义，式（2）还有其他形式。由于S0不能直接从测井资料获得，KC公式的应用受到了限制。

Timur提出了渗透率与孔隙度、束缚水饱和度的关系式［7］

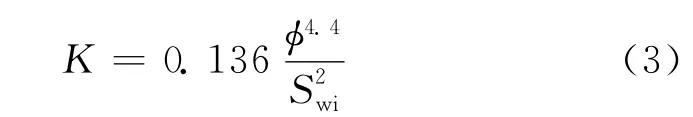
式中，Swi为束缚水饱和度，%。如果用孔隙度和自由流体指数Iff代替束缚水饱和度，得到式（3）的另一种变形［8］。变形后的参数可以通过NMR测井资料获得，从而可以计算渗透率。式（3）中束缚水饱和度可在一定程度上反映孔隙结构的变化。

对于单相流体而言，岩石渗透率应该只与孔隙系统有关系，而与岩石骨架没有关系。但是从实验中发现，对于一个固定的孔隙度值，渗透率的变化可以达到4个数量级。因此，还有其他因素对渗透率有着重要的影响。这些因素包括孔隙喉道半径、孔隙表面积、岩石颗粒的粒度和分选性、颗粒堆积的非均匀性。

Krumbein W C和Monk G D给出了砂岩渗透率与颗粒分选性及平均粒径的关系［9］

式中，d为岩石颗粒的平均直径，μm；σ为岩石颗粒的标准偏差；c为常数。式（4）表明岩石渗透率与颗粒平均直径的平方成正比，与颗粒分选性成反比。

杨建等［10］根据毛细管束模型的渗透率表达式，应用分形模型计算了松散砂岩的渗透率

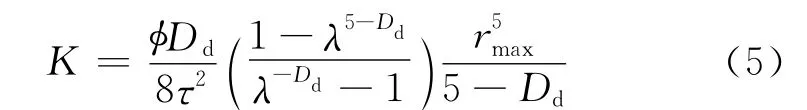
式中，τ为多孔介质孔隙迂曲度；λ为最小孔隙半径与最大孔隙半径之比；rmax为最大孔隙半径，μm；Dd为孔径分维数。

矿物组成的变化常常伴随沉积颗粒大小、形状和位置的改变，这些因素会影响岩石的孔隙系统，从而矿物组成的变化最终会影响岩石的渗透率。研究矿物组成与渗透率的关系，主要考虑3个方面的内容：黏土矿物对渗透率的影响，胶结矿物对渗透率的影响，矿物聚集形态和结构对渗透率的影响。其中黏土矿物主要影响Kozeny－Carman公式中岩石的比表面积和Timur公式中的束缚水饱和度，从而影响岩石的渗透率。胶结矿物含量直接影响孔隙的大小和形态，一般会降低岩石的渗透率和孔隙度。岩石结构对孔隙系统有直接影响，最终影响渗透率。

Herron M M和Rd O Q提出了一个考虑矿物组成的渗透率模型［3］

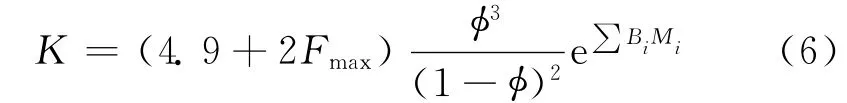
式中，Mi为第i种矿物的质量百分数，%；Bi为对应于第i种矿物的常数；Fmax为区域最大的长石含量，%。Mi可以通过地球化学测井方法得到，其他参数通过岩心刻度获得。该公式最引人注意的地方在于Fmax和Bi在不同区块具有基本确定的值，因而具有通用性，可以提高渗透率的预测精度。

对于碎屑岩储集层，用Kozeny－Carman公式计算渗透率比较合适，因为成岩作用过程引起了孔隙空间表面包裹黏土和矿物的变化，这些变化在KC公式中都可以定量描述。对于碳酸盐岩储层，通过测井资料预测其渗透率是一个非常棘手的问题。砂岩渗透率与孔隙度具有较好的相关性，但碳酸盐岩渗透率与孔隙度的相关性并不明显。基于碎屑岩得到的渗透率公式应用于碳酸盐岩并不能得到很好的效果，因此需要构建新的模型。碳酸盐岩渗透率模型的建立需要深入研究其微观结构，进而得到内部孔隙参数对渗透率的影响，最终建立渗透率模型。

通过测井测量参数转换为渗透率主要基于所有孔隙都是粒间孔隙的假设［11］，像碳酸盐岩这种具有复杂次生孔隙系统和微孔隙的岩石不满足这一假设。一般来讲，碳酸盐岩的渗透性主要受孔隙配位数、孔隙几何因子和孔隙喉道半径的影响。

孔隙配位数对渗透率的影响很早就引起了重视，Wyllie和Gardner［12－13］提出孔隙连通性是影响渗透率的主要因素。Stout等［14］用压汞的方法首次定量研究了碳酸盐岩孔隙空间的连通性。孔隙配位数很难得到，但孔隙的连通性却可定量表征，就碳酸盐岩来讲，束缚水饱和度Swi和有效孔隙度与总孔隙度之比（φe／φt），都可以反映孔隙的连通性。

孔隙横截面积对地层因素和渗透率具有重要影响［15］。Watfa［16］的研究表明，孔隙横截面积的变化与胶结指数m成反比关系，胶结指数m与渗透率成反比关系。由于Archie公式在测井解释中的广泛应用，地层因素与孔隙度的关系人们很早就知道，但地层因素与渗透率的关系却知者甚少。一般来讲，地层因素变大，渗透率就会变小。究其原因，碳酸盐岩中溶洞填隙物和胶结物会堵塞孔隙，不连通的孔隙的增多会增大胶结指数m，减小孔隙度，最终增大地层因素，而不连通的孔隙会引起渗透率降低。

控制孔隙喉道半径对碳酸盐岩的渗透性起主要作用，一般通过压汞曲线确定，Schowalter［17］和Thompson［18］用R10确定，Pittman［19］用R35确定，也有学者［20］用其他部分确定控制孔隙喉道半径。

李兵等［21］通过制作碳酸盐岩薄片，拍摄微观孔隙裂隙的环境扫描电镜（ESEM）照片，采用数字图像分析获取孔隙度、平均半径等相关的统计数据。给出渗透率模型式（7）

式中，¯r为平均孔隙半径，μm。

Mowers和Budd［22］利用岩石图像分析技术，从白云岩岩心塞薄片数字图像中测量现存孔隙体系的孔隙面积及比表面，单个像素分辨率略小于1μm。根据孔隙面积估算孔隙度，应用Kozeny－Carman公式，导出关于孔隙面积和比表面与岩心渗透率的经验方程

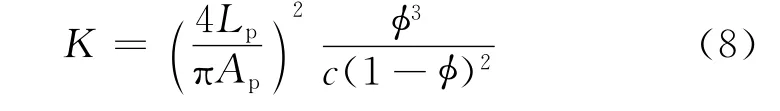
式中，Lp为孔隙周长，μm；Ap为孔隙面积，μm2；c为孔隙结构常数。

由于压汞实验可以得到岩心的孔径分布，因此也被用来建立渗透率模型。廖明光等［23］通过大量压汞实验数据，建立了渗透率模型

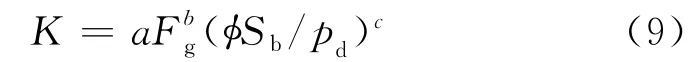
式中，Fg为孔隙几何因子；Sb为无穷大压力时汞饱和度，%；pd为外推排驱压力，MPa；a、b、c为经验常数。该估算模型可以较好地估算岩样的渗透率。在实际应用中，特别是对于应用岩屑毛细管压力曲线确定岩屑的渗透率有实际意义，因为岩屑难以用常规方法测定渗透率。

Dziuba［24］根据实验研究，提出了计算碳酸盐岩渗透率公式

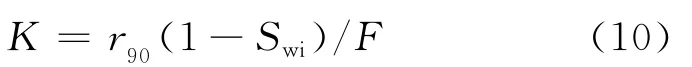
式中，r90为压汞曲线上汞饱和度90%对应的孔隙半径，μm；Swi为束缚水饱和度，%；F为地层因素。这些参数通过测井和岩心测量得到。

对于含有孔洞的碳酸盐岩，孔洞连通性系数是渗透率大小的一个标志。由于孔洞孔隙度的增加，孔洞连通性和半径也会随着增加。Xu C M等［25］根据电成像测井资料提出了渗透率模型

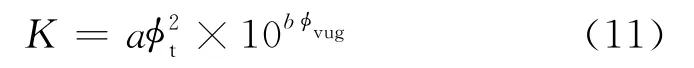
式中，φt为总孔隙度，%；φvug为孔洞孔隙度，%。其中总孔隙度和孔洞孔隙度可以通过电成像测井资料处理得到。对于孔洞不发育的层段，式（11）中第1项对渗透率起主要作用；对于孔洞发育的层段，孔洞对渗透率的影响成指数关系。

对于含有铸模孔的粒状灰岩，Ertas D等［26］提出了一个新的渗透率模型。具体思路：首先应用CT技术构建岩心的三维孔隙结构，通过对三维孔隙结构的分析，揭示了相邻铸模孔壁厚度是影响铸模粒状灰岩渗透率的主要因素；其次应用NMR技术的T2谱分布，通过颗粒尺寸和铸模孔隙度得到了平均的相邻铸模孔壁厚度；最后建立了渗透率与平均铸模孔壁厚度的关系式。具体形式为

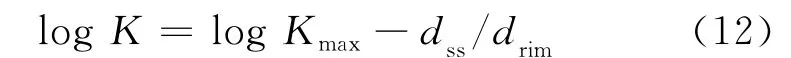
式中，Kmax为铸模孔壁接近0时的渗透率，mD；dss为平均的相邻铸模孔壁厚度，是颗粒尺寸和铸模孔隙度的函数，μm；drim为每个铸模孔的平均边长，μm。与常用的Coates模型和SDR模型计算的渗透率相比，式（12）计算的渗透率均方差更小，计算结果更精确。

1.2 双重孔隙介质的渗透率模型

双重孔隙介质的孔隙空间由原生粒间孔隙和次生裂缝2种孔隙构成，含有裂缝的双重孔隙介质的渗透率定义与单重孔隙介质的渗透率定义一致。但是渗透率进一步细化为基质渗透率和裂缝渗透率。基质渗透率与单重介质的相同，裂缝渗透率受多种因素影响，主要包括裂缝孔隙度、裂缝张开度、裂缝密度、裂缝倾角和裂缝长度等。由于实际裂缝储集层中裂缝的分布极为复杂，要建立双重孔隙介质的渗透率模型，必须对裂缝系统进行简化，建立简化模型。裂缝储集层的简化模型主要有平行板模型［27］，Kazemi模型［28］和Warren－Root模型［29］。

平行板模型将实际模型简化为由水平基质层和裂缝相互交替组成，但不考虑基岩的渗透率，裂缝渗透率可用式（13）计算

式中，φf为裂缝孔隙度，%；bf为裂缝张开度，μm。

Kazemi模型将实际模型简化为由水平基质层和裂缝相互交替组成，其总渗透率为基岩渗透率和裂缝渗透率之和，公式推导过程中假设裂缝面与y轴垂直，具体形式为

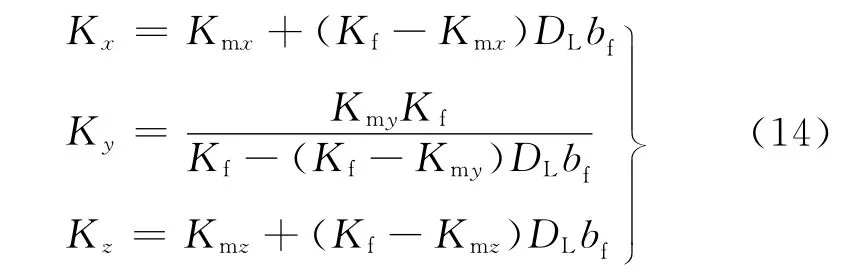
式中，Kx、Ky、Kz分别为裂缝性岩层直角坐标系3个坐标轴方向总的渗透率，mD；Kmx、Kmy、Kmz分别为直角坐标系3个坐标轴方向的基岩渗透率，mD；Kf为裂缝渗透率，mD；DL为裂缝线密度；bf为裂缝张开度，μm。

Warren－Root模型将双重孔隙介质油藏简化为正交裂缝切割基岩岩块呈六面体的地质模型，裂缝方向与主渗透率方向一致，并假设裂缝宽度为一个常数。裂缝网络可以是均匀分布，也可以是非均匀分布，采用非均匀分布的裂缝网络可以研究裂缝网络的各向异性或在某一方向上变化的情况。具体渗透率可用式（15）计算［30］

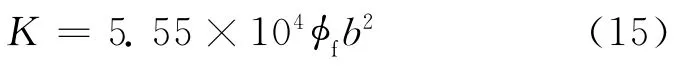
简化情况下推导得到的渗透率模型不能反映真实情况下的渗透率，只是一种理论性的模型。有的学者提出了更一般化的渗透率模型。Parsons考虑了裂缝的数量和裂缝与流体渗流方向间的夹角，提

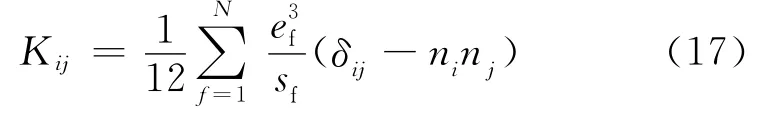
式中，Kij为渗透率张量分量，mD；ni、nj（i，j＝1，2，3）为裂缝f的法向方向余弦；δij为狄拉克符号；ef为平均裂缝张开度，μm；sf为裂缝间距，μm；N为裂缝数量。Snow公式是建立在裂缝无限大的假设基础上，不能应用于裂缝有限大的情况。Oda［33］引入裂缝张量的概念（裂缝张量是裂缝密度、裂缝张开度、裂缝方向和裂缝面积的函数），导出了球形域的渗透率张量公式出模型［31］

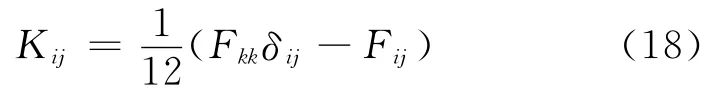
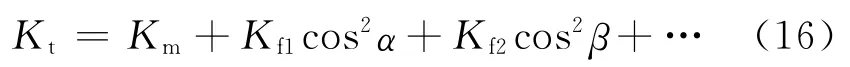
式中，Kt为岩石的总渗透率，mD；Km为基岩渗透率，mD；Kfi为裂缝i与流体渗流方向夹角为0时的裂缝渗透率，mD；α、β为裂缝与流体渗流方向夹角，（°）。

双重孔隙介质油藏的渗透率一般具有非均质性和各向异性的特点，表现在渗透率的具体表达形式上具有张量的形式。渗透率张量理论是20世纪60年代由美国学者Snow［32］提出，Snow导出了具有可变方向的N条裂缝组成岩石的渗透率张量形式

式中，F为裂缝张量；δij为狄拉克符号。Oda公式扩展了Snow公式的应用范围，可以应用于裂缝有限大的情况，但是不再显式地含有连通性这个对建立裂缝网络非常关键的参数。Doolin和Mauldon［34］建立了含有正交裂缝网络二维岩层的渗透率模型。他们假设岩石是分层的，相邻的2个层之间有裂缝，每1个单独的层也含有垂直于裂缝面的不同分布的裂缝，与层间裂缝组成1个正交的裂缝网络。他们提出的具体模型为

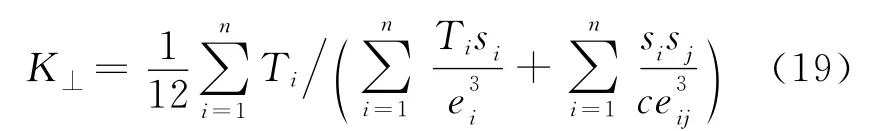
式中，K⊥为垂直于岩层的渗透率，mD；Ti为第i个岩层的厚度，m；si为第i个岩层中相邻裂缝的平均距离，m；ei为第i个岩层平均裂缝张开度，m；eij为相邻岩层i与j层间裂缝的张开度，m；c为常数。

最近，应用随机和分形方法计算裂缝性岩石的渗透率值得一提，同登科等［35］建立了求解对地层应力敏感的分形介质渗透率的数学模型，并采用了一种简单的技巧获得其近似解

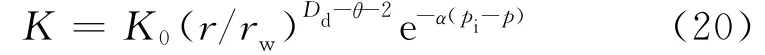
式中，K0为初始渗透率，mD；α为渗透率模数；p为压力，psi＊＊非法定计量单位，1psi＝6 894.757Pa，下同；pi为初始压力，psi；θ为分形指数；r为径向距离，m；rw为井径，m；Dd为孔径分维数。模型表明渗透率与压力间的关系按照指数规律变化，与井眼距离间的关系按幂律变化。

Jiajie Chen［36］基于岩心提出了裂缝的定量表征方法并分析了双重孔隙介质渗透率的影响因素。Schlumberger公司采用FMI资料和Chen的裂缝表征方法，提出了渗透率模型

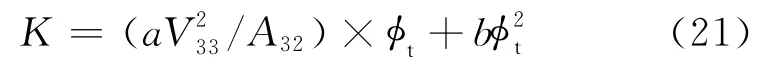
式中，K为FMI测井渗透率，mD；V33为单位体积岩心中裂缝的体积，m3／m3；A32为单位体积岩心中裂缝的面积，m2／m3；a、b为常数；φt为总孔隙度。

Jafari和Babadagli［37］应用多元回归分析的方法，综合运用测井、露头和试井资料，提出了以随机属性、分形属性和试井渗透率为独立变量的渗透率模型

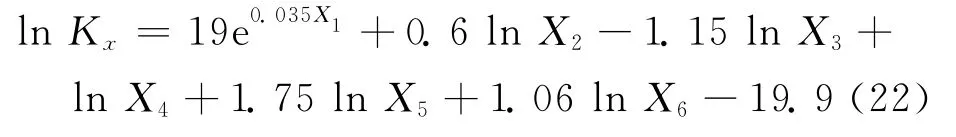
式中，Kx为x方向的渗透率，mD；X1、X5为分形属性参数；X2、X3、X4为随机属性参数；X6为试井渗透率，mD。

2 渗透率模型建模中存在的问题

（1）渗透率建模的理论研究欠缺。关于渗流理论主要有毛细管束理论和Darcy定律。毛细管束理论将复杂的岩石对象抽象为等径或不等径的毛细管，然后采用Hagen－Poisseuille流动方程进行流动模拟，由于不能反映真实的岩石内部结构，因而据此建立的渗透率模型预测精度有限。Darcy定律是渗流力学中一个经典的公式，但应用时要注意Darcy定律也有局限性，当流动速度变大（比如岩石裂缝发育）或流体黏度变大（比如稠油油藏）时，将不满足Darcy定律，这时的流动是一种非Darcy流。由于毛细管束理论和Darcy定律的局限性，现在一般通过分析各种影响因素对渗透率的影响，然后通过统计学方法建立渗透率模型。由于没有理论研究做指导，建立的渗透率模型的应用范围较小，精度不高。

（2）没有提出通用的渗透率模型。岩石的岩性多样，内部结构复杂，影响渗透率的因素很多，许多学者提出了不同的渗透率模型，应用于具有不同特性的岩石，至今没有提出一个通用统一的渗透率模型。刘向君等［38］在充分分析现有渗透率预测模型的基础上，尝试提出一个通用的渗透率模型。模型自变量选用孔隙度和反映泥质含量的参数，采用多项式形式

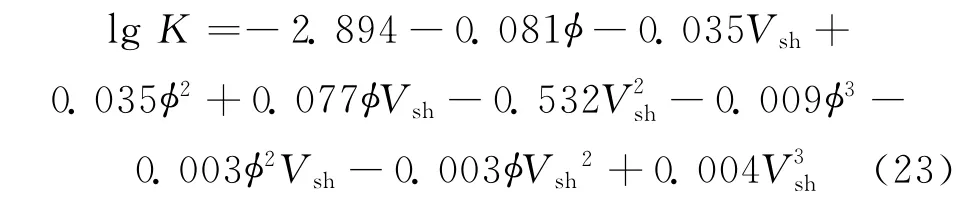
式中，Vsh为泥质含量，%。式（23）适用于碎屑岩，不能应用于碳酸盐岩等油藏，且该式中不含影响渗透率的孔隙结构参数，因而并不是真正的通用模型。

（3）双重孔隙介质渗透率模型亟待发展。一般碳酸盐岩油藏都发育裂缝，一些特低渗透率油藏也需要通过压裂来提高采收率。目前关于双重孔隙介质的渗透率模型却多数从简化模型导出，不能应用于实际油田开发。裂缝参数的准确获取有望解决含油裂缝岩石渗透率的建模问题。

3 展 望

（1）基于岩心二维薄片图像或三维CT扫描，出现了建立岩心的三维数字图像的技术，称为数字岩心技术。通过对岩心进行数字化，应用数值模拟的方法得到渗透率。由于数字岩心技术可以真实地再现岩石的微观孔隙结构，因此对研究渗透率具有明显的优势，有望建立通用统一的渗透率模型。赵秀才［39］应用CT技术建立了三维孔隙网络模型，最后采用LATTICE－BOLTZMANN方法直接进行三维流动模拟，通过Darcy定律计算渗透率。刘学峰［40］也做了这方面的工作，不过都没有提出各自的渗透率模型，需要进一步发展。

（2）岩石的弛豫时间谱与岩石的孔径分布能够较好地吻合，可以用激发极化弛豫时间谱表征孔隙结构。激发极化弛豫时间谱反映了岩石的孔径分布，一旦孔径分布确定，即可采用不同的模型得到渗透率。童茂松等［41］采用奇异值分解法对泥质砂岩的激发极化衰减谱进行多指数反演，得到光滑连续的激发极化弛豫时间谱，并据此给出了渗透率模型。此外，分形理论和电成像测井应用于含有裂缝地层的裂缝特征提取，有助于解决裂缝性岩石的渗透率建模问题。

［1］ Anselmetti F S，Luthi S，Eberli G P.Quantitative Characterization of Carbonate Pore Systems by Digital Image Analysis［J］.AAPG Bulletin，1998，82（10）：1815－1836.

［2］ 闫国亮，王殿生，刘金玉，等.基于均匀化方法的周期性缝洞型介质渗透率的数值计算［J］.煤炭学报，2011，36（9）：1446－1450.

［3］ Herron M M，Rd O Q.Estimating the Intrinsic Permeability of Clastic Sediments from Geochemical Data［C］∥SPWLA 28th Annual Symposium，1987，paper HH.

［4］ Kozeny J.Ueber Kapillare Leitung des Wassers im Boden［J］.Sitzungsberichte Wiener Akademie，1927，136（2a）：271－306.

［5］ Carman P C.Fluid Flow Through Granular Beds［C］∥Transactions.Institution of Chemical Engineers，1937，15：150－166.

［6］ Scheidegger A E.The Physics of Flow Through Porous Media［M］.New York：Macmillan，1960.

［7］ Timur A.An Investigation of Permeability，Porosity，and Residual Water Saturation Relationships［C］∥SPWLA 9th Annual Symposium，1968，paper J.

［8］ Timur A.Producible Porosity and Permeability of Sandstone Investigated Through Nuclear Magnetic Resonance Principles［J］.The Log Analyst，1969，X（1）：3－11.

［9］ Krumbein W C，Monk G D.Permeability as a Function of the Size Parameters of Unconsolidated Sand［C］∥SPE 943153，1942.

［10］杨建，陈家军，杨周喜，等.松散砂粒孔隙结构、孔隙分形特征及渗透率研究［J］.水文地质工程地质，2008，35（3）：93－98.

［11］Babadagli T，Al－Salmi S.A Review of Permeability Prediction Methods for Carbonate Reservoirs Using Well－log Data［C］∥SPE 87824，2004.

［12］Wyllie M R J，Gardner G H F.The Generalized Kozeny－Carman Equation：part I［J］.World Oil，1958，146（4）：121－126.

［13］Wyllie M R J，Gardner G H F.The Generalized Kozeny－Carman Equation：part II［J］.World Oil，1958，146（5）：210－228.

［14］Stout J L.Pore Geometry as Related to Carbonate Stratigraphic Traps［J］.AAPG Bulletin，1964，48（3）：329－337.

［15］Towle G.An Analysis of the Formation Resistivity Factor－Porosity Relationship of Some Assumed Pore Geometries［C］∥SPWLA 3rd Annual Symposium，1962.

［16］Watfa M.Current Affairs in Saturation［J］.Middle East Well Evaluation Review，1987（2）：49－57.

［17］Schowalter T T.Mechanics of Secondary Hydrocarbon Migration and Entrapment［J］.AAPG Bulletin，1979，63（5）：723－760.

［18］Thompson A H，Katz A J，Raschke R A.Estimation of Absolute Permeability from Capillary Pressure Measurements［C］∥SPE 16794，1987.

［19］Pittman E D.Relationship of Porosity and Permeability to Various Parameters Derived from Mercury Injection－Capillary Pressure Curves for Sandstone［J］.AAPG Bulletin，1992，76（2）：191－198.

［20］Nelson P H.Permeability－Porosity Relationships in Sedimentary Rocks［J］.The Log Analyst，1994，35（3）：38－62.

［21］李兵，凌其聪，鲍征宇，等.用数字化图像分析法确定岩石物性［J］.新疆石油地质，2008，29（2）：253－255.

［22］Mowers T T，Budd D A.Quantification of Porosity and Permeability Reduction Due to Calcite Cementation Using Computer－assisted Petrographic Image Analysis Techniques［J］.AAPG Bulletin，1996，80（3）：309－322.

［23］廖明光，李士伦，付晓文.储层岩石渗透率估算模型的建立［J］.天然气工业，2001，21（4）：45－48.

［24］Dziuba T T.Improved Permeability Prediction in Carbonates［C］∥SPWLA 37th Annual Symposium，1996.

［25］Xu C M，Russel D，Gournay J，et al.Porosity Partitioning and Permeability Quantification in Vuggy Carbonate Using Wireline Logs，Permian Basin，West Texas［C］∥SPWLA 46th Annual Symposium，2005.

［26］Ertas D，Zhou M Y，Dunsmuir J H.Permeability Controls on Moldic Grainstones：CT Based Pore Network Modeling of Carbonate Reservoir Rock from West Texas and a New NMR－based Permeability Transform［C］∥SPWLA 47th Annual Symposium，2006.

［27］Lomize G M.Flow in Fractured Rocks［M］.Moscow：Gesenergoizdat，1951.

［28］Kazemi H.Pressure Transient Analysis of Naturally Fractured Reservoir with Uniform Fracture Distribution［C］∥SPE 2156，1969.

［29］Warren J E，Root P J.The Behaviors of Naturally Fractured Reservoir［C］∥SPE 426，1963.

［30］Reiss L H.The Reservoir Engineering Aspects of Fractured Formations［M］.France：Imprimerie Louis－Jean，1980：20－22.

［31］秦积舜，李爱芬.油层物理学［M］.东营：中国石油大学出版社，2006：140.

［32］Snow D T.Anisotropic Permeability of Fractured Media［J］.Water Resources Research，1969，5（6）：1273－1289.

［33］Oda M.Permeability Tensor for Discontinuous Rock Mass［J］.Geotechnique，1985，35（4）：483－495.

［34］Doolin D M，Mauldon M.Bed－normal Permeability in Fractured Sedimentary Rock［C］∥North American Rock Mechanics Symposium 2rd，1996.

［35］同登科，周德华，陈钦雷.具有应力敏感于地层渗透率的分形油气藏渗流问题的近似解析研究［J］.石油勘探与开发，1999，26（3）：53－57.

［36］Jiajie（Jeff）Chen.Deriving Quantitative Fracture Properties from Whole Core Description：A Practical Link Between Geological Observation and Flow Simulation［C］∥SPE130725，2010.

［37］Jafari A，Babadagli T.Generating 3DPermeability Map of Fracture Networks Using Well，Outcrop，and Pressure－Transient data［C］∥SPE124077，2011.

［38］刘向君，夏宏泉，赵正文.砂泥岩地层渗透率预测通用计算模型［J］.西南石油学院学报，1999，21（1）：10－14.

［39］赵秀才.数字岩心及孔隙网络模型重构方法研究［D］.青岛：中国石油大学，2009：132.

［40］刘学峰.基于数字岩心的岩石声电特性微观数值模拟研究［D］.青岛：中国石油大学，2010：115.

［41］童茂松，李莉，王伟男，等.岩石激发极化弛豫时间谱与孔隙结构、渗透率的关系［J］.地球物理学报，2005，48（3）：710－716.

Review on Absolute Permeability Model

SUN Jianmeng，YAN Guoliang
（School of Geosciences，China University of Petroleum，Qingdao，Shandong 266555，China）

Introduced is current permeability model about single porosity media and dual porosity media.There exist some problems in permeability model，such as lacking theoretical researches，no uniform model and model of dual porosity media also needs urgently developing.Permeability and porosity of single porosity media have good correlation，but porosity is not the only parameter which is crucial to the accurate permeability model，and therefore other parameters of rock structure and pore structure should be considered.Permeability model about dual porosity media can be divided into matrix permeability and fracture permeability，and the coupling of them is critical for permeability model.The application of fractal theory and imaging well logging may improve the accuracy of dual porosity media modeling.Beside this，the application of 3Ddigital core technology and induced polarization method are the importance in permeability model construction.

log interpretation，petrophysical property，permeability model，single porosity media，dual porosity media，research progress，digital core

P631.84 文献标识码：A

国家重大专项复杂裂缝性碳酸盐岩油藏开发关键技术研究资助（2008ZX05014－004－006HZ）

孙建孟，男，1964年生，教授，博士生导师，从事测井资料处理、解释与岩石物理研究。

2011－12－21 本文编辑 王小宁）