主动同步法实现Mathieu方程的混沌同步

刘晓君，李险峰，党红刚，刘 莉

（1.天水师范学院数学与统计学院，甘肃 天水 741001；

2.兰州交通大学数理与软件工程学院，甘肃 兰州 730070）

主动同步法实现Mathieu方程的混沌同步

刘晓君1，李险峰2，党红刚1，刘 莉1

（1.天水师范学院数学与统计学院，甘肃 天水 741001；

2.兰州交通大学数理与软件工程学院，甘肃 兰州 730070）

首先通过全局分岔图和吸引子图对所研究的Mathieu方程的动力学行为进行了分析.在此基础上，对该方程的混沌同步进行了研究.利用主动同步方法实现了2个不同初值的Mathieu方程间的自同步，同时利用该方法实现了Mathieu方程与非线性陀螺系统间的异结构同步.数值仿真验证了该方法对实现Mathieu方程混沌同步的有效性.

Mathieu方程；混沌；主动同步；误差系统

Mathieu方程是一类含有激振力并带有多个系数的非线性方程，具有丰富的动力学行为.因该方程能够描述较为普遍的工程问题，如大型结构支承顶杆的抗震问题，内燃机配气挺杆横振和油田井架钻杆的横振等［1］.因此对其深入研究不仅具有一定的理论意义，也具有重要的实用价值.

自从混沌同步被提出以来，就在很多领域得到了较为广泛的应用［2－6］，已经成为了科学领域的研究热点问题之一.但一般的同步方法都是针对自治系统提出的，适合于非自治系统的同步方法却比较少，而且由于非自治系统形式都较复杂，实现与其他系统间的异结构同步就更加困难.针对于此，本文利用文献［7］中提出的主动同步法，对著名的Mathieu方程的同步进行了研究.不仅利用该方法实现了2个不同初值的Mathieu方程间的自同步，同时实现了Mathieu方程与非线性陀螺系统间的异结构同步.数值仿真验证了该方法对非自治系统的有效性.

1 Mathieu方程的混沌

本文研究的一类Mathieu的方程为［8］：

这是一个非自治的时间连续系统，其中δ，μ，n1，β1，β2，β3，β4，ε，α1，α2和ω1为系统的参数.变量x1表示位移，x2表示速率，˙x2为加速度.

通过四阶变步长Rung-Kutta方法，数值仿真出系统以周期激振力ε作为分岔参数在［7，10.5］区间内变化的全局分岔图.随着参数ε的逐渐增大，可以发现系统发生了倍周期分岔（见图1）.

当参数取值为：δ＝0.5，n1＝3，μ＝3，β1＝5，β2＝0.7，α1＝1，α2＝1，β3＝0.5，β4＝0.5，ε＝10.5，ω2＝2，初值为（0.3，－0.15）时，系统（1）此时处于混沌运动，存在混沌吸引子，计算机模拟的该吸引子见图2.

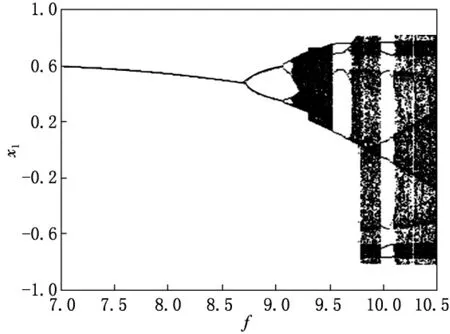
图1 以周期激振力ε为控制参数的分岔图

2 主动同步

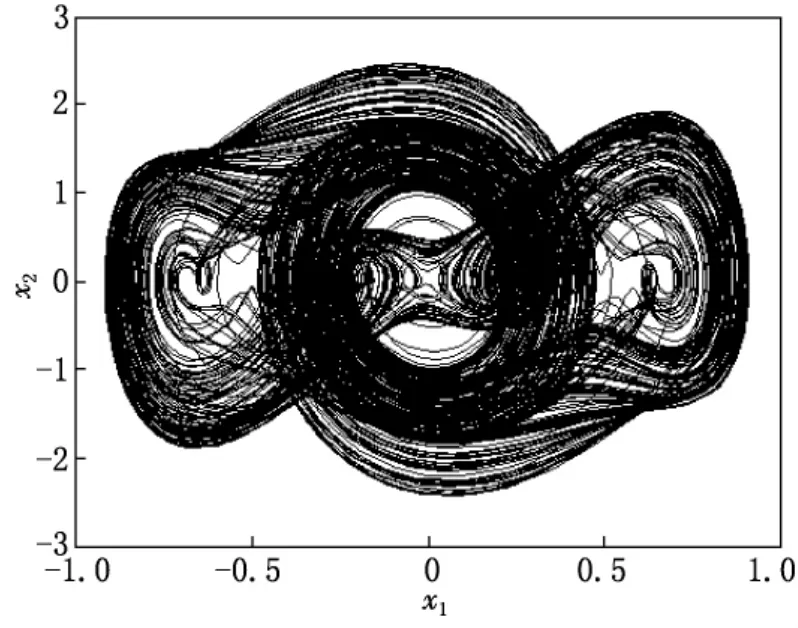
图2 ε＝10.5时的混沌吸引子

利用文献［7］中的主动同步法分别研究系统（1）的自同步与异同步.

2.1 自同步

系统（1）与系统（2）即可达到自同步.计算可得当d1＝0，d2＝2，d3＝17，d4＝0时，可满足条件（6）式.

取系统参数为δ＝0.5，n1＝3，μ＝3，β1＝5，β2＝0.7，β3＝0.5，β4＝0.5，α1＝1，α2＝1，ε＝10.5，ω1＝2.驱动系统和响应系统的初值分别为x0＝（－0.3，0.15）和y0＝（0.3，－0.2），两者均位于相同的吸引域内.数值仿真可得同步误差收敛曲线（见图3）.从图3中可以看到控制器使得驱动与响应系统达到了同步.

2.2 异同步

为了实现Mathieu方程的异结构同步，选用陀螺系统作为驱动系统.因为非线性陀螺系统是非常特别的一类非自治系统，由于其在结构、体积、成本方面的优势而广泛应用在航空、航天、航海和陆地车辆的导航与定位及油田勘探等军事、民用领域中［9］.由于陀螺仪是惯性导航和惯性制导系统的基本测量元件，因此，其高精度、高质量的工作性能与惯性系统所提供的载体姿态参数和导航定位参数的准确性息息相关.其力学模型如图4所示.

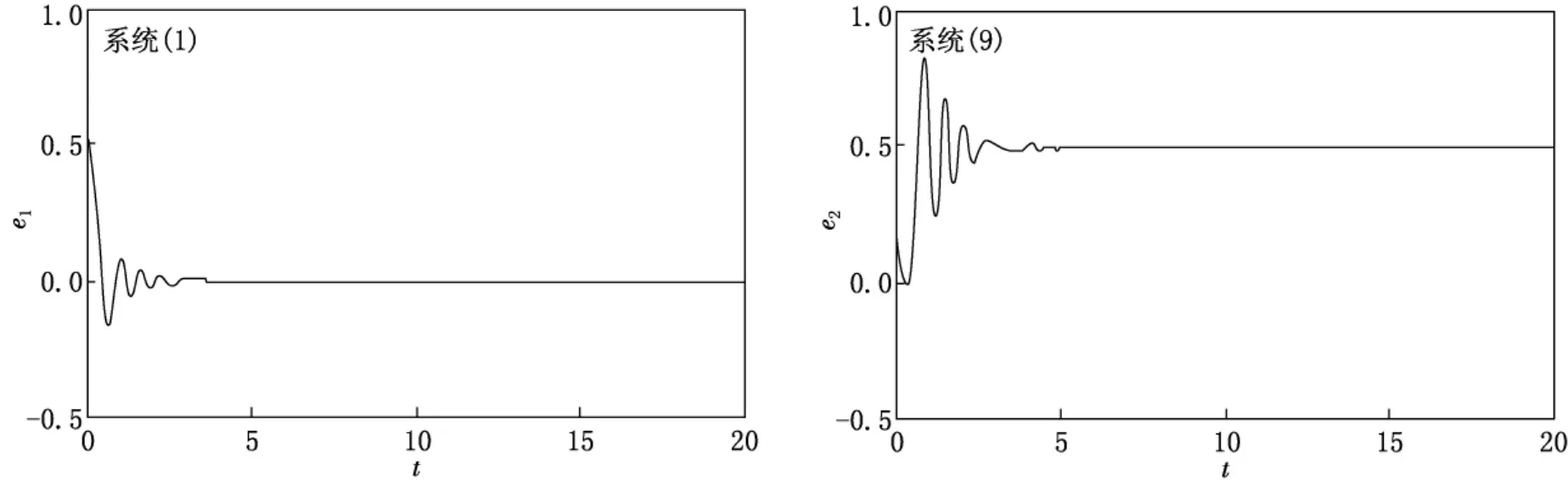
图3 系统（1）与系统（9）的同步误差曲线

图4 非线性陀螺仪的力学模型子

图5 非线性陀螺系统的吸引子

驱动系统和响应系统的初值分别为x0＝（1，－1）和y0＝（－0.3，0.15），数值仿真可得同步误差收敛曲线（如图6所示）.从图6中可以看到控制器使得驱动系统（7）与响应系统（8）在t＝4s左右快速达到了同步.

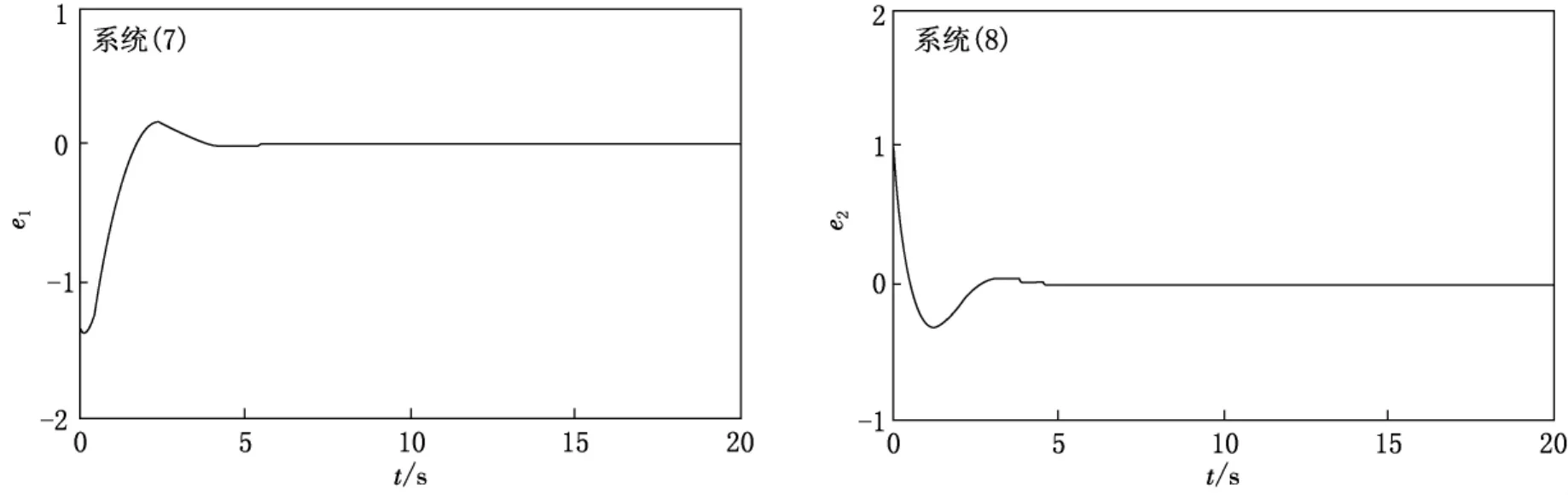
图6 同步误差收敛曲线

3 结论

本文对Mathieu方程的混沌同步进行了研究，采用主动控制方法实现了2个不同初值的Mathieu方程间的自同步，在此基础上，利用主动同步方法实现了Mathieu方程与非线性陀螺系统间的异结构同步.Mathieu方程可以描述很多工程问题，所以对其混沌同步研究具有重要的意义.

［1］ 陈予恕，梅林涛.非线性参数振动系统的共振分叉解［J］.中国科学，1990，9：938-945.

［2］ PECORA LM，CARROLL TL.Synchronization in chaotic systems［J］.Phys Rev Lett，1990，64（8）：821-824.

［3］ KOCREV L，PARLITZ U.Generalized synchronization，predictability and equivalence of unidirectionally coupled system［J］.Phys Rev Lett，1996，76（11）：1816-1819.

［4］ VINCENT UE，NJAH AN，AKINLADE O，et al.Phase synchronization in unidirectionally coupled chaotic ratchets［J］.Chaos，2004，14（4）：1018-1025.

［5］ LIAO TL.Adaptive synchronization of two Lorenz systems［J］.Chaos Solitons and Fractals，1998，9：1555-1561.

［6］ CHEN HK.Global chaos synchronization of a new chaotic system via nonlinear control［J］.Chaos Solitons and Fractals，2005，23：1245-1251.

［7］ 刘晓君，李险峰，韩秀萍.新的主动同步方法控制参数激励混沌系统［J］.河北师范大学学报：自然科学版，2010，34（1）：36-41.

［8］ 李险峰，褚衍东，刘晓君，等.控制 Mathieu方程中混沌的三种方法分析［J］.振动与冲击，2007，26（1）：35-37.

［9］ YAU HT.Chaos synchronization of two uncertain chaotic nonlinear gyros using fuzzy sliding mode control［J］.Mechanical Systems and Signal Processing，2008，22：408-418.

The chaos synchronization of the mathieu function based on the active synchronization method

LIU Xiao-jun1，LI Xian-feng2，DANG Hong－gang1，LIU Li1

（1.School of Mathematics and Statistics，Tianshui Normal College，Tianshui 741001，China；
2.School of Mathematics，Physics ＆Software Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

In the paper，the dynamics of the Mathieu function is studied through the global bifurcation diagram and attractor.The chaos synchronization of the Mathieu function is investigated.First，the self-synchronization of two Mathieu function with different initial conditions is realized by the active synchronization method.The active synchronization of the nonlinear gyros system and the Mathieu function is achieved by the active synchronization.Numerical simulations show that the method is effective for the Mathieu function.

Mathieu function；chaos；active synchronization；error system

O 322

110·44

A

1000-1832（2012）01-0067-05

2011-07-05

甘肃省自然科学基金资助项目（096RJZE106）；天水师范学院科研基金资助项目 （TSA1012）.

刘晓君（1980—），女，硕士，讲师，主要从事非线性系统建模与数值计算.

石绍庆）