可测横截集及小波框架

张新成，黄运生，李 想

(1.开封大学软件技术学院，河南开封 475004;2.开封教育学院数学系，河南开封 475000; 3.开封大学学报编辑部，河南开封 475004)

可测横截集及小波框架

张新成1，黄运生2，李 想3

(1.开封大学软件技术学院，河南开封 475004;2.开封教育学院数学系，河南开封 475000; 3.开封大学学报编辑部，河南开封 475004)

定义和刻画了空间L2(R2)中的可测横截集被，利用可测横截集的理论，得到一个小波框架，而且它的对偶也是小波框架，最后构造了广义的Shannon小波基.

可测横截集;标准正交基;小波框架

0 引言

构造小波的主要方法是多分辨分析法(MRA)［1］，其优点是保证了小波有分解和重构的快速算法.近年来，小波框架也成为小波分析研究的热点之一.紧小波框架作为正交小波的推广保持了正交小波基除正交性以外几乎所有优良的性质.而且，它是一种冗余的重构系统，这在信号处理的某些领域发挥着重要的作用.文献［2］奠定了小波框架的一般理论基础，刻画了小波框架的完全特征，从理论上证明了基于MRA方法的小波框架能从任何尺度函数导出.之后，出现了研究小波框架的热潮［3－4］.

抽样定理在通信理论研究和数字信号处理应用中起着重要的作用.应用最广的抽样定理是古典Shannon抽样定理［5］，古典Shannon抽样定理主要适用于带限信号，即信号f(x)的Fourier变换限于区域［－l，l］，且满足Nyquist抽样频率时，f(x)可由它的规则抽样准确重构.后来人们把古典Shannon抽样定理应用到了平移不变子空间［6］和小波子空间中［7－8］.文献［9］提出和刻画了空间L2(R)中可测横截集的概念.利用发展的理论，作者得到了广义的类Shannon抽样定理.

由于现实中的图像都是高维的，因此我们把可测横截集理论推广到L2(R2)空间中.首先，定义L2(R2)可测横截集概念，然后研究了高维可测横截集的性质，接着利用可测横截集的理论，构造了一个具有良好性质的小波框架，而且还证明了它的对偶也是小波框架.

1 概念

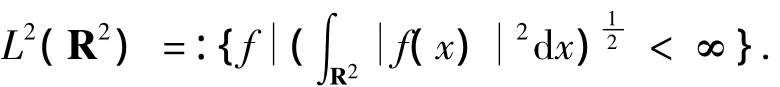
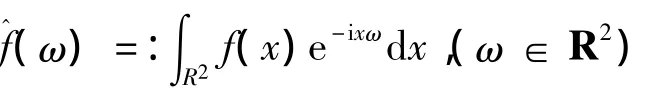
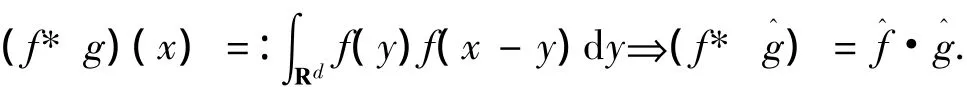
另外，约定表示可测集E⊂R的Lebesgue测度.χE(x)表示在E上为1，而在其他的点为0的函数.函数f的支撑指的是集合{(x)≠0}的闭包，记为suppf.

2 二维空间可测横截集的定义与性质

2.1 高维空间可测横截集的定义

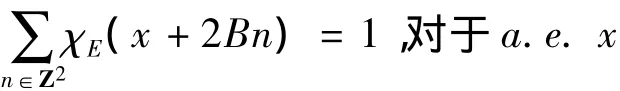
2.2 二维空间可测横截集的性质

性质1如果可测集E是B－横截的，则有

(1)除去一个零测度集外，{E+2Bn}n∈Z2构成一簇不相交的R2的剖分，即∩{E+2Bn}=φ，∪{E+2Bn}=R2;

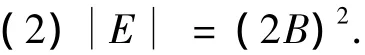
证明 (1)结论是明显的.

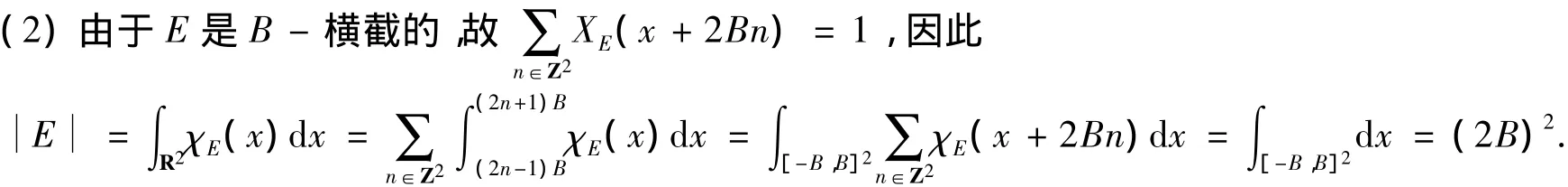
利用可测横截集的概念，可以得到一个标准正交基，这是文献［9］中结果的推广.

定理1令E⊆R2且E是B－横截的;对于k∈Z，定义ek∈L2(E)如下

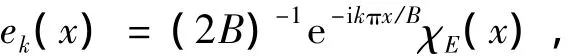
则{ek}k∈Z是L2(E)的标准正交基，且如果F∈L2(E)，则有

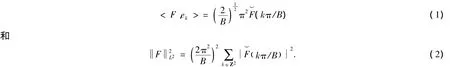
证明先证标准正交性.由E是B－横截的，故

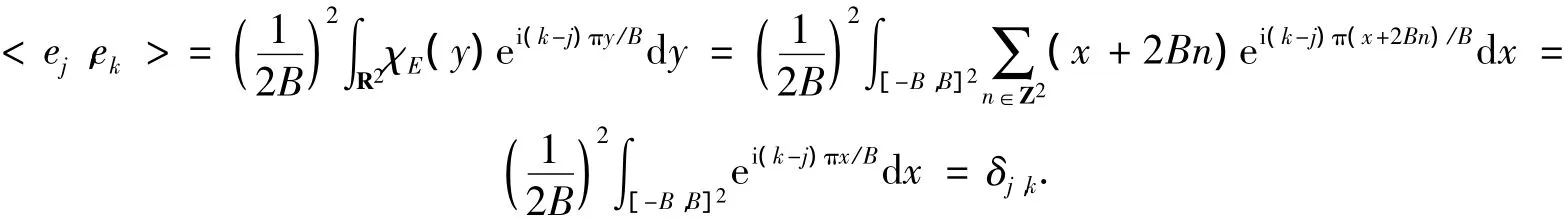
再证明完备性.设F∈L2(E)，且＜F，ek＞=0，k∈Z，由于suppf⊂E，故FχE=F，因此

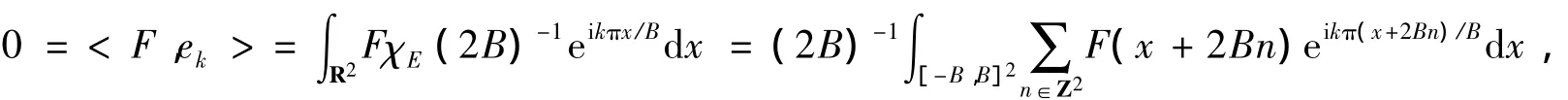
即，对于任意的k∈Z，有

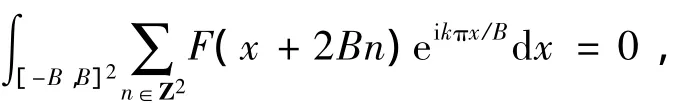
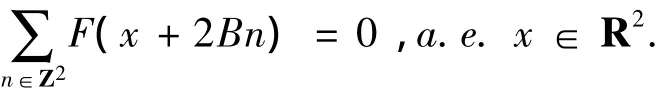
又由于suppf⊂E，而E是B－横截的，故{F(x+2Bn)}n的支集不相交，所以，对任意n∈Z2，有

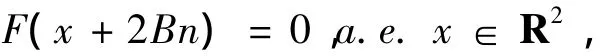
特别地F=0.由此证明了完备性.

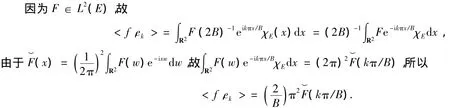
又由于{ek}是L2(E)的标准正交基，故由Parseval等式可知，

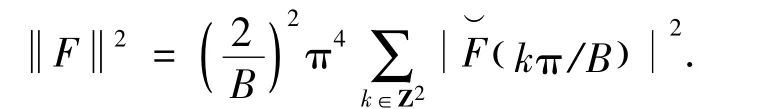
即式(1)、式(2)成立.

下面，利用可测横截集的概念和定理1，能得到相应函数空间卷积的一个性质.

定理2设E⊂R是B－的横截的，f，g∈L2，sup⊂E，sup⊂E，则有

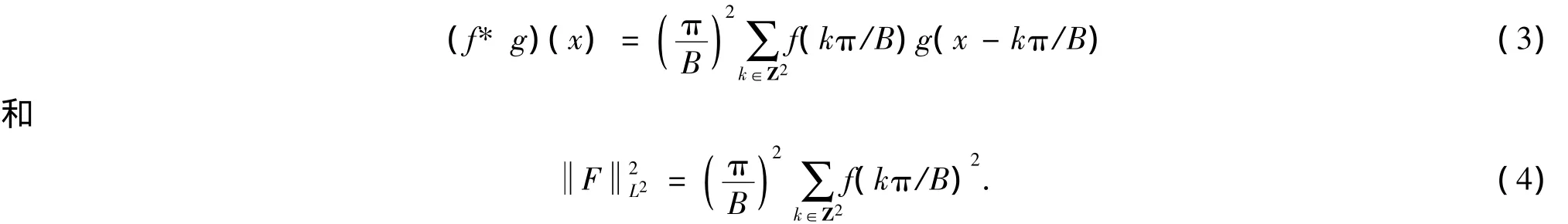
证明令，则F∈L2(E)，由定理1可知

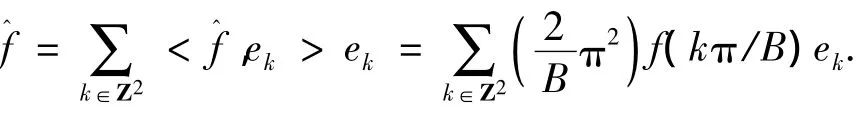
把上式代入卷积的性质f*g=)，则有

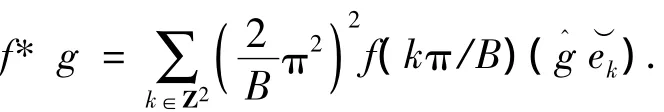
利用Fourier变换的性质有［g(x－kπ］=(2B)，故

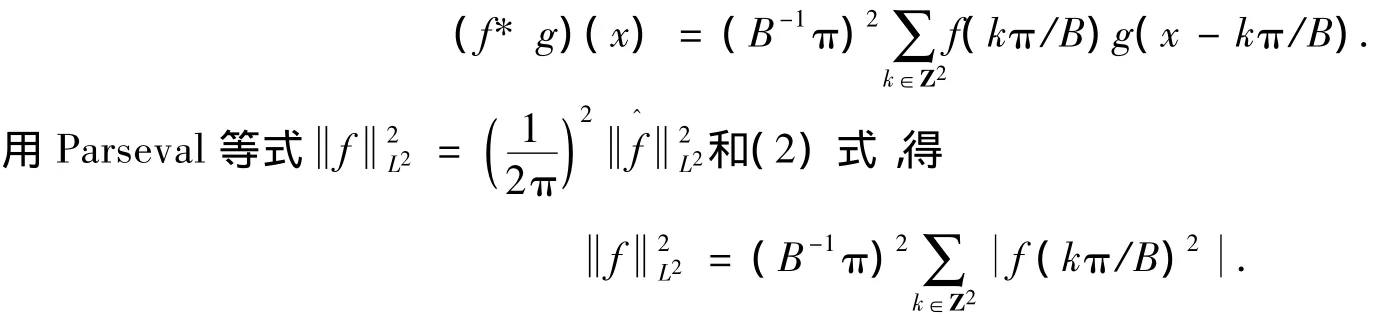
定理证毕.

下面我们将利用横截集的概念得到一个小波框架，而且证明它的对偶也是小波框架.

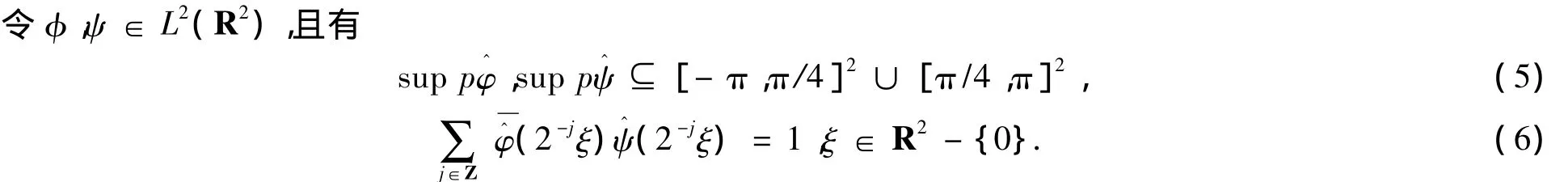
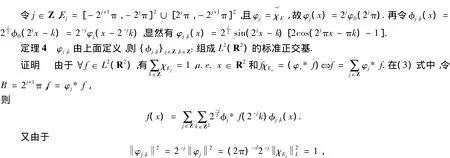
由定理1可知定理4成立.

3 结语

尽管本文的概念和一些结果是文献［9］的推广，但在定理推导中，我们使用了一些新的方法，并且得到了一些新的结果，比如定理3和定理4.这为理论在图像处理中的应用提供了可能.

［1］ 崔锦泰.小波分析导论［M］.程正兴，译.西安:西安交通大学出版社，1995.

［2］ BENEDETTO J J，LI S.The theory of multiresolution analysis frames and application to filter banks［J］.Appl Comp Harm Anal，1998，5(4): 398－427.

［3］ DAUBECHIES I，HAN B，RON A，et al.Framelets:MRA－based constructions of wavelet frames［J］.Appl Comput Harmon Anal，2003，14(1):1－46.

［4］ WU GUOCHANG，CHENG ZHENGXING，LI DENGFENG，et al.Parseval frame wavelets associated with A－FMRA［J］.Chaos，Solitons＆Fractals，2008，37(4):1233－1243.

［5］ SHANNON C E.Communication in the presence of noise［J］.Proc IRE，1949，37(1):10－21.

［6］ CHEN W，ITOH S.A sampling theorem for shift invariant subspaces［J］.IEEE Trans Signal Process，1998，10(46):2822－2824.

［7］ XIA XIANGGEN，ZHANG ZHEN.On sampling theorem，wavelet and wavelet transforms［J］.IEEE Trans Signal Process，1993，41(12):3524－3535.

［8］ WU GUOCHANG，CHENG ZHENGXING，YANG XIAOHUI.The cardinal orthogonal scaling function and sampling theorem in the wavelet subspaces［J］.Appl Math Comput，2007，194(1):199－214.

［9］ BENEDETTO J J.Frame decompositions，sampling，and uncertainty principle inequalities［M］//BENEDETTO J，FRAZIER M.Wavelets: Mathematics and Applications.Boca Raton:CRC Press，1993.

Measurable Transversal Set and Wavelet Frame

ZHANG Xin-cheng1，HUANG Yun-sheng2，LI Xiang3

(1.College of Software Technology，Kaifeng University，Kaifen475004，China;2.Department of Mathematics，
Kaifeng Institute of Education，Kaifen475000，China;2.Editorial Department，Kaifeng University，Kaifeng475004，China)

The measurable transversal set of spaceL2(R)2is defined.By the theory of the measurable transversal set，a wavelet frame is obtained.Furthermore，its dual frame is also a wavelet frame.At last，a general Shannon wavelet base is constructed.

measurable transversal set;orthonormal basis;wavelet frame

O174.2

A

1007－0834(2012)01－0017－05

10.3969/j.issn.1007－0834.2012.01.006

2012－01－04

张新成(1982—)，男，河南叶县人，开封大学软件技术学院副教授，主要研究方向:数据库及软件开发.