几何凸函数的两个充要条件及其应用*

陈少元，宋振云

（1.湖北职业技术学院 公共课部，湖北 孝感 432000；2.湖北职业技术学院 信息技术学院，湖北 孝感 432000）

几何凸函数的两个充要条件及其应用*

陈少元1，宋振云2

（1.湖北职业技术学院 公共课部，湖北 孝感 432000；2.湖北职业技术学院 信息技术学院，湖北 孝感 432000）

利用几何凸函数的几何凸性，研究了几何凸函数的判定条件和特性，通过构建辅助凸函数的方法，建立了几何凸函数的两个充要条件，并给出了其应用.

几何凸函数；充要条件；应用

MSC 2000：26D15 52A40

0 引言及预备知识

函数的凸性在控制论、线性规划、最优化理论中有着广泛的应用.随着应用的深入，又推动了函数凸性的研究，从而使函数凸性的研究成为一个热点.作为函数凸性研究的一个重要方面，如函数的Schur凸性，文献［1］讨论了一类对称函数的Schur凸性和凹性，建立了若干不等式.文献［2］在介绍了几何凸函数的概念之后，着重介绍了两种判定方法——函数变换法和导数判别法.文献［3］进一步研究了几何凸函数的算术运算性质和函数运算性质，给出了几何凸函数的六种判别方法和几何凸函数的Jensen型不等式.本文在上述研究的基础上，应用凸函数的概念，根据几何凸函数的定义，通过构建辅助凸函数，建立了几何凸函数的两个充要条件，并讨论了其应用.

定义1［3～5］设f（x）是定义在区间I⊂R＋上的正值函数，若 ∀x1，x2∈I，∀t∈ ［0，1］，有：

则称f（x）是区间I上的几何凸函数.若不等式（1）中的不等号反向，则称f（x）是区间I上的几何凹函数.

1 定理及其证明

定理1 设I⊂R＋是有限区间，f∶I→R＋，则函数f（x）在I上是几何凸（凹）函数的充分必要条件是：上的凸（凹）函数.

则

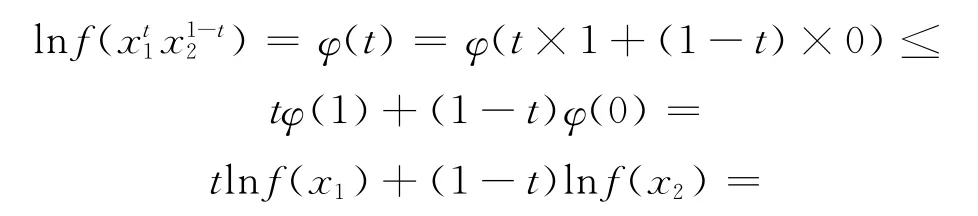
2 应用举例

例1［3］设f（x）是定义在区间I∈R＋上的正值函数，且f（x）在I上具有二阶导数，则f（x）为I上的几何凸（凹）函数的充要条件是：

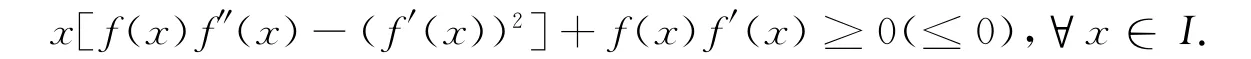
证明 仅证f（x）是I上的几何凸函数的情形，同理可证f（x）是几何凹函数的情形.

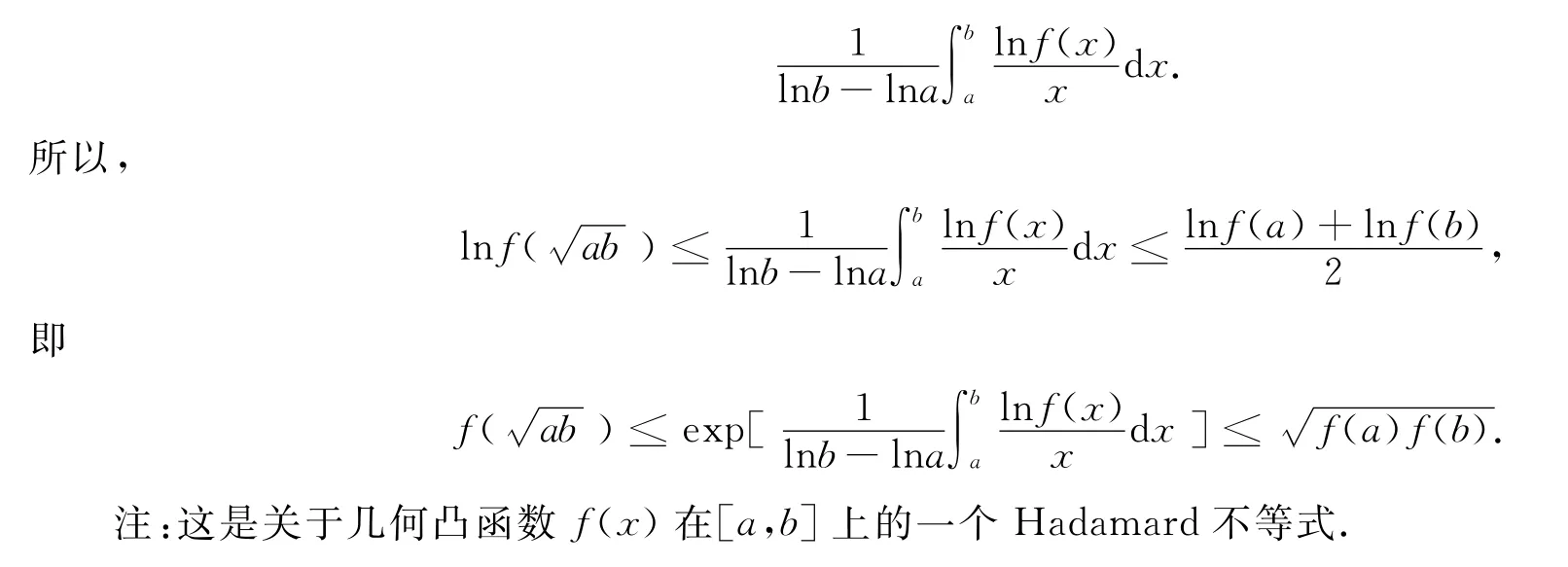
［1］褚玉明，夏卫锋，赵铁洪.一类对称函数的Schur凸性 ［J］.中国科学（A辑），2009，39（11）：1267～1277.

［2］张小明.几何凸函数 ［M］.合肥：安徽大学出版社，2004：15～17，64.

［3］吴善和.几何凸函数与琴生不等式 ［J］.数学的实践与认识，2004，34（2）：155～163.

［4］张小明.几何凸函数的几个定理及其应用 ［J］.首都师范大学学报（自然科学版），2004，25（2）：11～13.

［5］杨露.关于几何凸函数的不等式 ［J］.河北大学学报（自然科学版），2002，22（4）：325～327.

［6］华云.关于 GA－凸函数的 Hadamard型不等式 ［J］.大学数学，2008，24（2）：147～149.

［7］宋振云.几何凸函数的几何平均型Hadamard不等式 ［J］.首都师范大学学报（自然科学版），2011（4）：15.

MSC 2000：26D15 52A40

Two Necessary and Sufficient Conditions and Application of Geometry Convex Functions

CHEN Shao-yuan1，SONG Zhen-yun2
（1.Common Curricule Department，Hubei Vocational ＆Technological College，Xiaogan 432000，China；2.School of Information Technology，Hubei Vocational ＆Technological College，Xiaogan 432000，China）

By studying the judgment conditions and properties of geometry convex functions based on their geometry convex and by constructing the auxiliary convex function method，the authors set up two necessary and sufficient conditions of geometry convex functions，and bring forth their applications.

geometry convex function；necessary and sufficient condition；application

O174.13

A

1009-1734（2012）01-0006-04

2012-01-15

湖北省教育科学“十二五”规划课题（2011B329）.

陈少元，副教授，从事高等数学教学及凸分析研究.