基于多元回归模型的叶面积指数遥感反演

宋亚斌，林 辉，孙 华，宁小斌

(1.中南林业科技大学，长沙 410004； 2.国家林业局中南林业调查规划设计院，长沙 410014)

基于多元回归模型的叶面积指数遥感反演

宋亚斌1，林 辉1，孙 华1，宁小斌2

(1.中南林业科技大学，长沙 410004； 2.国家林业局中南林业调查规划设计院，长沙 410014)

采用2011年8月获取的黄丰桥林场SPOT5数据为信息源，并同步开展现地样地调查，依据典型抽样，以不同的海拔、坡度、坡向进行选样,利用手持GPS和LAI-2000植物冠层分析仪，分别对选取的60块样地进行定位和叶面积指数测量。结合遥感数据和实地调查数据，对地理因子和遥感因子变量进行主成分分析，采用逐步回归法筛选出2个主成分建立多元回归方程，对该研究区域的植被叶面积指数进行模拟，精度达到84.17%。结果表明：RVI，NDVI，MSAVI，MCAVI和DVI与LAI之间存在较好的相关性。

遥感；多元回归模型；参数反演；叶面积指数；SPOT5

叶面积指数是单位水平地面面积上所有叶子投影面积的总和，是估计植物冠层功能的一个重要参数，是认识和掌握植物冠层空隙的动态和平衡的重要指标，也是生态系统中最重要的结构参数之一[1,2]。叶面积指数直接反映出在多样化尺度的冠层尺度中的能量、二氧化碳及物质循环，也与许多生态过程，如蒸散量、土壤水分平衡、生产力等直接相关，它的变化体现了植被生长发育的不同状态[3]。因此，精确确定林分的叶面积指数，无论在森林经营与管理还是在森林生态环境的研究中都具有重要的意义。

对于叶面积指数的测定，由于受其定义、采样方法、仪器误差、人力和物力等多种因素影响，至今国内外还没有通用简单的测量方法，现有的方法只能在局部范围内进行测量。采用遥感技术，则能快速、准确且大范围获取叶面积指数。卫星遥感具有宏观性、综合性、短周期性、可重复性和低成本等特点，用其进行地区尺度的森林资源定量估测，可以节省大量的人力、物力和财力，提高工作效率。由于受大气、地理位置、土壤及植物本身光化学反应变化等因素影响，使得地物光谱反射率与叶面积指数的关系具有一定的地域性和时效性。简单实用的叶面积指数反演方法及反演精度的提高已成为当前研究的热点和难点[4]。

以样地调查资料及对应的SPOT5遥感数据和1∶1万地形图为主要信息源，遥感因子与地理因子相结合，以湖南省株洲市攸县黄丰桥林场的植被为研究对象，用多元回归法对其进行叶面积指数反演，旨在提高叶面积指数的提取效率，为评价或验证用遥感数据反演叶面积指数的可靠性提供参考。

1 研究区概况与数据获取

1.1 研究区概况

黄丰桥林场地处湖南省株洲市攸县东部，位于13°04′—113°43′E， 27°06′—27°24′N。属亚热带季风湿润气候区，年平均气温17.8℃，年降水量1410.8mm，无霜期292 d左右；以中低山貌为主，最高海拔1270m，最低海拔115m，坡度20°～35°，土壤以板页岩发育而成的山地黄壤为主。林场境内森林茂盛，物种丰富，有木本植物430余种。

1.2 数据获取

1.2.1 外业数据采集

由于森林类型、海拔、坡向、坡度与森林叶面积密切相关，不同的森林类型、海拔、坡度、坡向，其植被有着不同的叶面积。采取典型抽样法，分别以不同的海拔、坡度、坡向进行选样。利用LAI-2000植物冠层分析仪，在60m×60m的样地范围内，分别样地4个角及样地中心位置设置10 m×10m样方测量LAI值，取5次测量的均值作为样地的LAI值。共选取60个样地，每个样地为1组数据，前40个数据用于建模，后20组用于检验模型精度。

1.2.2 遥感数据源

遥感数据为2011年7月10日获取的研究区SPOT5原始多光谱数据，与样地外业采集的时间基本同步。

2 数据处理

2.1 辐射校正

在遥感成像时，由于存在大气对电磁波辐射的散射和吸收、太阳高度与传感器观察角的变化以及地形起伏引起的辐射强度变化等影响因素，使得遥感图像产生辐射误差，即灰度失真。尽管地面站提供的产品已经经过了系统辐射校正，消除了遥感器系统产生的辐射畸变，但仍存在着大气散射和吸收引起的辐射误差及太阳高度角的地形等光照条件差异引起的辐射误差[5]。此次研究使用ENVI4.8软件采用辐亮度法对研究区影像进行辐射定标后，再用FLAASH模块进行大气校正，校正效果明显。

2.2 几何精校正

在完成对研究区数据辐射校正的基础上，还需进行几何精校正。利用ENVI4.8几何校正模块，以研究区1∶1万地形图为标准空间，选取影像和地形图上都清晰的、能精确定位的地物点作为控制点，且尽量均匀分布。本次几何精校正残差达到0.32，小于0.5个像元，校正后影像与地形图叠合效果很好，满足此次研究需求。

2.3 DEM制作

采用研究区等高距为5m的1∶1万地形图，通过ArcGIS10.0软件对其进行矢量化后，用空间分析扩展模块制作成分辨率为2.5m的DEM，用以提取建模所需的样地地理因子。

2.4 建模因子信息提取

影响植被叶面积的因素有很多，如坡向、坡度、海拔、树种组成、树龄、树高、胸径、郁闭度等。因此,估测模型变量的设置是利用RS和GIS技术进行叶面积指数定量估测的关键之一。

根据植物的波谱反射曲线及SPOT5数据的特点：SP1波段所在的近红外反射区受叶片内部结构的影响，对近红外辐射的反射很强烈；SP2波段区有一个小的反射峰；SP3波段是叶绿素的吸收带；SP4所在的短波红外对土壤湿度、植被覆盖和树叶含水量很敏感，能更有效地区分林地或作物的排列方式，对植被类型的反应更准确[6,7]。植被指数是多光谱遥感数据经过分析运算产生的对植被长势、森林结构参数等有一定指示意义的数值，其可以用一种简单有效的形式来实现对植被状态信息的表达。植被指数的定量测量可表明植被活力，而且植被指数比单波段用来探测森林结构参数有更好的灵敏性[8,9]。

综合上述分析，此次研究选取：坡向、海拔、坡度、SP1，SP3，SP4以及比值植被指数(RVI)、归一化植被指数(NDVI)、修正的土壤调节植被指数(MSAVI)、修正的叶绿素调节植被指数(MCARI)、差值植被指数(DVI)等11个因子，作为构建叶面积指数估测模型的变量因子，利用ENVI4.8及ArcGIS10.0软件提取样地因子信息。

3 数据分析与建模

3.1 主成分分析

为避免输入自变量数据之间所具有的相关性对模型预测精度的影响，减少输入的数据量，在建模型前，对选取的11个建模因子信息进行主成分分析。共建立了拥有11个变量的数据库，结果见表1。通过SPSS对选取的11个变量进行主成分提取，结果见表2和表3。

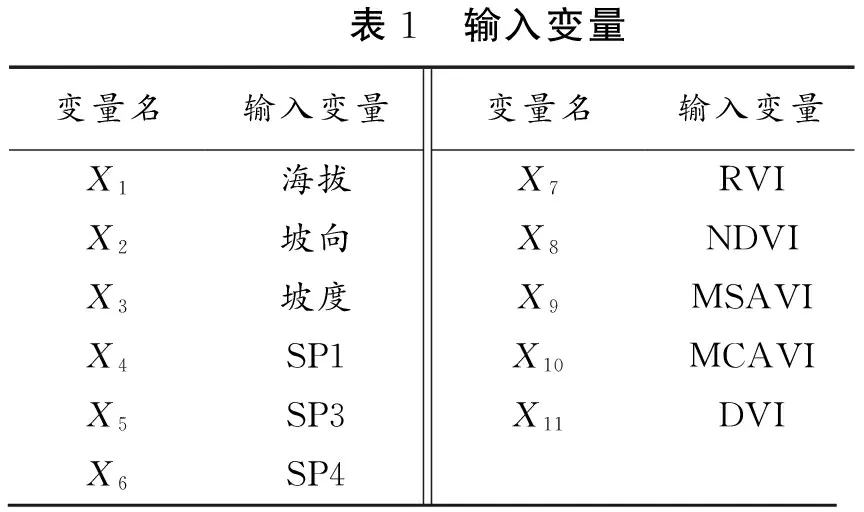
表1 输入变量变量名输入变量变量名输入变量X1海拔X7RVIX2坡向X8NDVIX3坡度X9MSAVIX4SP1X10MCAVIX5SP3X11DVIX6SP4

表2 主成分系数矩阵变量名主成分F1F2F3F4F5F6F7X10.108 -0.480 -0.334 0.607 0.398 0.346 0.0130X2-0.0230-0.3820.750-0.3020.02600.4470.00400X3-0.0420-0.5050.5940.3940.149-0.4610X4-0.8210.4410.1720.288-0.05700.06100.0270X50.2390.7590.3380.460-0.1400.1350.0300X60.1040.5220.109-0.2630.794-0.07400.00800X70.9700.07300.04400.0760-0.004000.0230-0.207X80.998-0.00400-0.002000.0140-0.0240-0.01400X90.991-0.0310-0.0110-0.0130-0.0390-0.01900.112X100.983-0.109-0.0290-0.0710-0.0240-0.04000.108X110.9540.2300.1320.0970-0.04300.0300-0.00500

表3 主成分累积贡献率主成分特征值累积贡献率/%主成分特征值累积贡献率/%F15.55050.46F70.0690099.72F21.74666.33F80.0260099.95F31.20277.26F90.00400099.99F40.99986.34F100.00100099.10F50.83993.97F110100F60.56399.09

3.2 主成分提取结果分析

各原始变量前面的系数大小说明了其在各主成分中所占重要性的大小，由表2可知，原始变量X4和X7～X11在第一主成分中起主要作用，且X4与第一主成分成负相关，而X7～X11与第一主成分成正相关；同理第二主成分中X1～X6的系数较大，起重要作用；X2和X3，X1和X5，X6，X1～X3，X7分别在第三、第四、第五、第六和第七主成分中起主要作用。

由表3可知，前7个主成分的累积贡献率达到了99.72%，基本包含了原始输入数据的所有信息，故取前7个主成分作为建模型的变量来代替原始变量，使建模变量从11个缩减为7个，从而达到建模型时减少输入数据量的目的。

3.3 构建叶面积指数反演模型

采用多元逐步回归分析法构建叶面积指数反演模型。多元逐步回归分析法是在多元回归分析的基础上发展起来的，其基本思想是根据自变量对因变量作用的大小，保留作用程度大的自变量，剔除作用程度小的自变量，从大量的可供选择的自变量中选取最重要的自变量，以此建立回归分析的估测模型。

3.3.1 提取模型自变量

在整个逐步回归分析过程中，变量的引入和剔除在两端是同时进行的，每一步的计算都需要进行F检验，并且根据F检验来判断该自变量是否应该被引入或剔除模型。设定一个显著性水平α,查F检验临界值Fα。当Fin值>Fα值，该变量被引入模型，否则剔除；与此同时，如果计算变量剔除的Fout值≤Fα，则在这个显著性水平下，该自变量被剔除，否则保留。如此循环往复地计算，直至无符合引入条件的自变量，也无符合剔除条件的自变量为止。

此次研究对7个备选自变量(F1～F7)进行逐步回归分析，最终筛选出两个自变量，且这两个变量构成的回归模型为

Y=-5.21×10-3F1-1.89×10-3F3+3.47

(1)

3.3.2 模型参数检验

采用逐步回归分析法构建模型，计算得出回归模型的各参数值，见表4。

表4 回归模型参数值模型回归系数回归系数标准误差R2R2修F值Tb03.4711.38×10-230.480F1b1-5.21×10-31.06×10-30.7940.71214.688-4.933F3b3-1.89×10-35.30×10-4-3.567

3.3.3 精度检验

利用20个检验样本数据，通过如下公式来检验回归模型的预测精度。

(2)

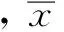
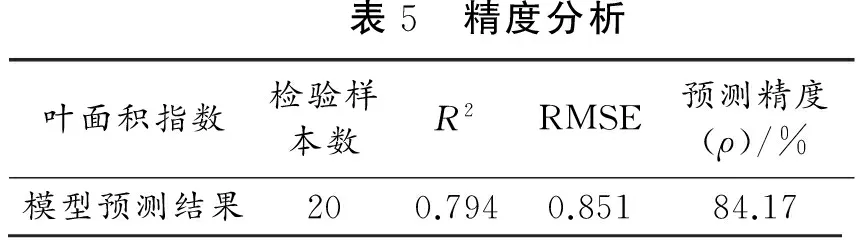
表5 精度分析叶面积指数检验样本数R2RMSE预测精度(ρ)/%模型预测结果200.7940.85184.17

图1 叶面积指数实测值与预测值

由表5可知，多元回归模型的判定系数为0.794，均方差为0.851，预测精度达到了84.17%，且模型通过了拟合优度检验、回归方程的显著性检验和回归系数的显著性检验，说明模型拟合效果良好，预测精度较高。

4 结论

通过多元回归方法，结合SPOT5遥感影像数据与森林调查数据，对黄丰桥林场的森林叶面积指数进行估测，采用主成分分析法对自变量进行降维处理，在减少运算量的同时也防止了自变量之间的相关性对模型估算精度的影响。由回归方程中的各主成分系数可知：RVI，NDVI，MSAVI，MCAVI，DVI与LAI都具有较好的相关性，且模型表现出了较高的判定系数和较好的回归拟合效果，预测精度达到了84.17%。结果表明，基于遥感技术来反演研究区植被叶面积指数是可行的，但这与一些研究中提到DVI与LAI相关性很差的结果并不一致，说明现今建立的LAI的估测模型在应用上存在很大的局限性，建立具有普遍适应性的模型是我们在今后相关研究的一个重要方向。

[1] 王秀珍,黄敬峰,李石梅,等.水稻叶面积指数的多光谱遥感估算模型研究[J].遥感技术与应用, 2003,18(2):57-65.

[2] 王希群,马履一,贾忠奎,等.叶面积指数的研究和应用进展[J].生态学杂志,2005,24(5):537-541.

[3] Holben B,Tueker C J,Fan C J. SPeetral Assessment of Soybean Leaf Area and Leaf Biomass[J].Photogrammetric Engineering and Remote Sensing.1980,46:311-326.

[4] 李开丽,蒋建军,茅荣正,等.植被叶面积指数遥感监测模型[J].生态学报,2005,25(6):1492.

[5] 赵英时,等.遥感应用分析原理与方法[M].北京:科学出版社,2003:172-180.

[6] 张宇,谷建才,等. 基于RS和GIS的径向基神经网络模型对森林蓄积量的估测[J].浙江林业科技, 2009,29(5):52.

[7] 刘宇光,金明,冯钟葵,等.SPOT数据反演地物辐射亮度和反射率的基础研究[J].地球信息科学,2005,7(2): 111-115.

[8] 张慧芳.北京地区森林植被生物量遥感反演及时空动态格局分析[D].北京:北京林业大学,2008:11.

[9] 程永政.多尺度农作物遥感检测方法及应用研究[D].郑州:解放军信息工程大学,2009:11-13.

TheInversionofLeafAreaIndexthroughRemoteSensingBasedontheMmultivariableRegressionModel

SONG Yabin1，LIN Hui1，SUN Hua1，NING Xiaobin2

(1.Central South University of Forestry & Technology，Changsha 410004，Hunan，China； 2.Central South Forest Inventory and Planning Institute of State Forestry Administration,Changsha，410014，Hunan，China)

remote sensing；multivariable regression model；parameter inversion；leaf area index；SPOT5

2012-03-15

国家林业局林业公益项目专题：林分结构与生长模拟技术研究(201104028)；湖南省高等学校科学研究项目“高分辨率遥感影像森林结构参数反演研究”(11C1313)。

宋亚斌(1987-)，男，浙江奉化人，硕士，主要从事林业遥感与地理信息系统应用研究。

TP79；S718.55

A

1003-6075(2012)02-0024-04

Abstyact： By using the SPOT5 image in Huangfengqiao forest farm which has been get in August 2011，we surveyed the sample plots at the same time, chose plots through different elevations, slopes and aspects based on typical sampling, then located the 60 sample plots to measure the leaf area index by using the GPS and LAI-2000 plant canopy analyzer. Based on the data of remote sensing and the sample plots, first to analyze eleven geographic and remote sensing factors which as input variables by using principal component analysis, and then a multiple regression equation was established by two principal components which were selected by stepwise regression, predicted the leaf area index of study area and the accuracy was 84.17%. Study results show that there has been a good correlation among RVI,NDVI, MSAVI, MCAVI, DVI and LAI.