竖缝式鱼道的弯道布置与结构形式研究
包 莉,安瑞冬
(1.中国水电顾问集团成都勘测设计研究院 水道处,四川 成都 610072;2.四川大学 水力学与山区河流开发保护国家重点实验室,四川 成都 610065)
1 前 言
当河流筑坝设闸后,人工建筑物将阻断天然河流的连通性,改变了其固有的自然特性,使鱼类栖息地环境因素(如水位、流量、水温等)出现变化,对鱼类活动产生重要影响,甚至阻断部分种群的洄游通道[1]。鱼道对于恢复鱼类及其他水生生物在河流中的自由通道具有重要意义,是流水生态改良的关键部件。现有鱼道形式主要包括丹尼尔式鱼道、池堰式鱼道和竖缝式鱼道[2]。
竖缝式鱼道利用隔板分成许多梯级池室,利用竖缝处射流与鱼池中水流的掺混来进行消能,该形式结构简单,维护与运行方便。鱼池中水流被突缩的竖缝壅高,动能部分转化为势能,从竖缝流出后在鱼池中剧烈掺混,大部分动能和势能再转化热能耗散[3]。数值模拟和物理模型实验是研究鱼道水力学特性的两种常见方法。
在鱼道实际设计中,为保证竖缝流速不高于鱼类冲刺泳速,底坡不宜过陡,而当上下游水位落差较大时会出现鱼道长度较长而超出场地布置区域的情况。这就需要对鱼道进行“折叠”,将鱼道设计成绕弯的形式。弯道中的流速应该足够小,以方便鱼类休息,且能起到平稳水流的作用。如果弯道处出现过大的流速或者弯道处水流流态紊乱,则会对鱼类洄游造成影响,对鱼道运行产生不良影响。
本文针对竖缝式鱼道的弯道进行研究,利用数值模拟的方法对比两种不同结构形式(圆弧形和矩形)的弯道,并进行了模型试验验证。
2 弯道鱼池布置与结构形式方案
研究针对我国西南地区某工程鱼道设计实例开展论证,拟建方案充分考虑鱼类游动能力及工程布置需求,鱼道竖缝宽度为0.3m,竖缝隔板倒角为45°,鱼道宽度2.0m,池室长度为2.4m,鱼池正常运行中水深为1.2m,其中每隔10级鱼池设置1休息池,休息池长度为4.8m,鱼道布置示意见图1。
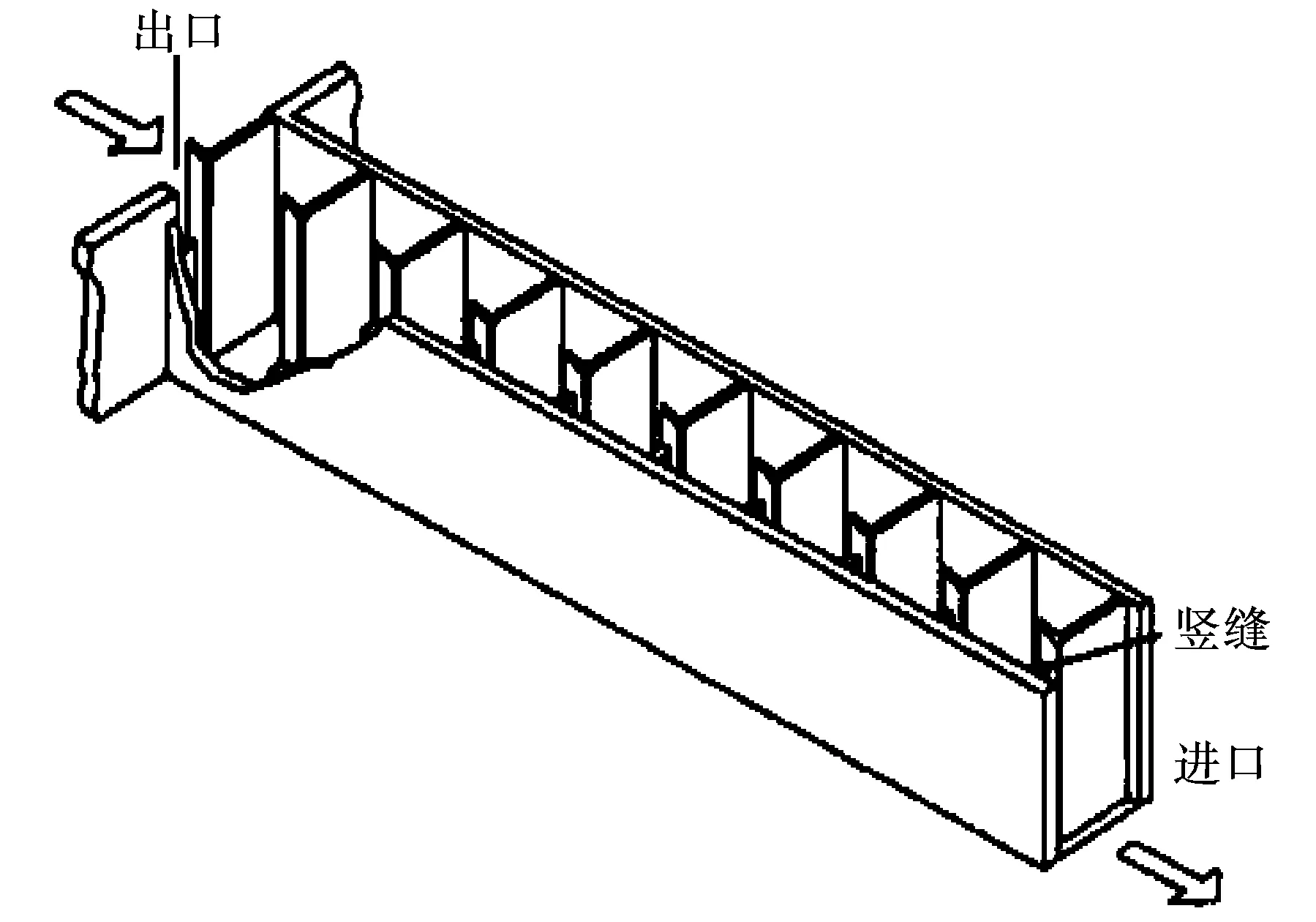
图1 竖缝式鱼道布置示意
在研究中发现,将鱼道弯道布置为休息池的方式可以减缓流态对洄游的不利影响。本文对两种不同结构形式的弯道进行研究,比较分析圆弧形弯道和矩形弯道的流态特点。
2.1 鱼类游动能力
洄游鱼类的游泳能力对于鱼道过鱼效果成功与否有着重要的影响。洄游鱼类的游泳能力主要由趋流特性和克流能力描述。
鱼类的趋流特性一般以感应流速为指标。感应流速指能够使鱼类产生趋流反应的流速值,感应流速通常以鱼类游动方向的改变为指示标准。鱼类的克流能力依生物代谢模式和持续时间的不同主要分为3类,以速度来表示:持续游泳速度、耐久游泳速度和突进游泳速度。
从鱼类游泳速度的角度来看,鱼道中的流速不宜过大,否则会给鱼类的洄游带来困难。本研究中鱼类突进游泳速度在1.1~1.25m/s范围。如何保障最大流速不超过鱼类突进游泳速度,鱼道结构形式的选择就十分重要。
2.2 圆弧形弯道方案及其特点
研究模型在圆弧形弯道的上、下游各设置三级竖缝式鱼池(见图2)。

图2 圆弧形弯道示意
该鱼道最显著的特点就是其弯道形式为圆弧形,上游竖缝式鱼池的水流的出射方向与圆弧形边墙的走向趋于平行。
2.3 矩形弯道方案及其特点
矩形弯道的与圆弧形弯道结构的鱼道一样,鱼池见图3。
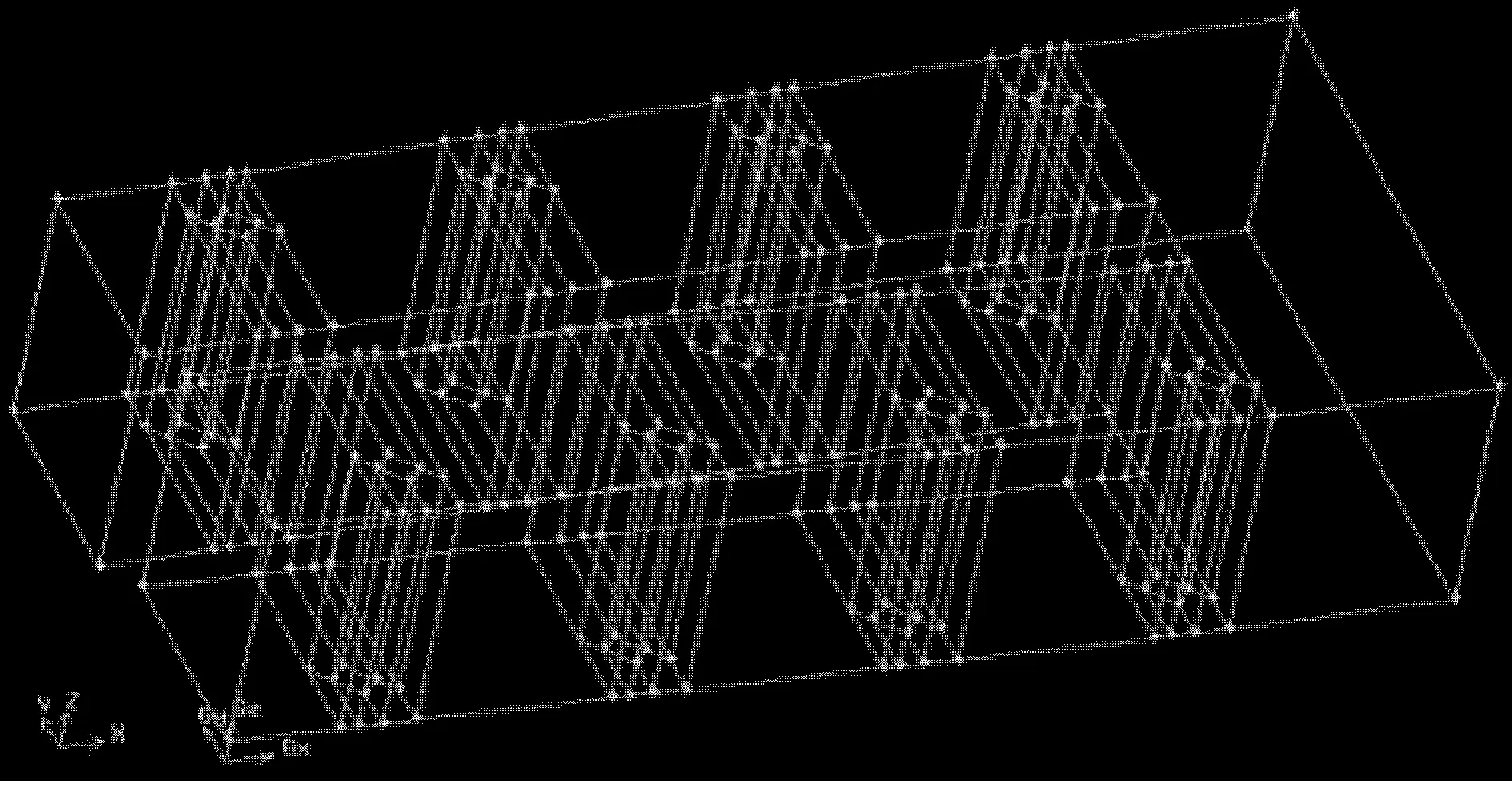
图3 矩形弯道示意
该鱼道最显著的特点是其弯道形式为矩形,上游竖缝式鱼池的水流出射后,趋向于矩形弯道的中心,且比圆弧形弯道的消能区域范围更大。
3 鱼道流态数值模拟
数值模拟要建立反映问题各物理量之间的微分方程及相应的定解条件。数值模型以前述设计资料为依据进行计算。根据鱼道水力学分析结论,研究了两种具有不同形式休息池的鱼道数值模拟,计算均在Q=0.360m3/s的流量下进行,水深为1.0m,模型坡度为S=2.6%。数值模拟主要通过使用FLUENT软件进行,选取三维计算模型。
3.1 数学模型
(1)连续方程;
(2)动量方程;
(3)紊动能k方程和耗散率ε方程。
3.2 数值模拟结果及分析
图4和图5分别给出圆弧形弯道和矩形弯道形式下,底层( 距底部0.2m)、中层( 距底部0.4m)和表层(距底部0.8m)的计算结果。
数值模拟结果表明:圆弧形弯道形式的鱼道竖缝处的最大流速能达到1.35m/s,矩形弯道形式的鱼道竖缝处的最大流速为1.20m/s。从流速的角度看,矩形弯道形式的鱼道流速较圆弧形弯道形式的鱼道小,更适于鱼类的洄游,且矩形弯道形式的鱼道靠近外侧边壁存在明显的回流区。圆弧形结构虽利于水流过流,却不利于掺混消能;而矩形结构增加局部糙率,利用了水流粘滞性,在休息池处消能作用明显,因此鱼道流速也相对较小,更利于鱼类洄游。
4 模型试验
4.1 模型布置
为了验证数值模拟计算的可靠性,进行了弯道矩形结构形式鱼道的模型试验。图6给出模型试验情况。弯道模型与计算模型尺寸保持一致,试验工况相同,而在长挡板末端增加沿上、下游方向的纵向挡板,形成“L”形结构形式。
4.2 矩形弯道休息池流速分布
主要对休息池进行流速的测量,图7为休息池流速等值线图。
由图7可知,矩形弯道休息池的最大流速为1.08m/s,方向为-45°。休息池中水流从竖缝流出后,主流沿竖缝方向流动,遇到挡板时被壅高,形成壅水并且转向,向下一级鱼池流动;由于水流从竖缝处出来后断面突然扩大,过水面积明显增大,主流两侧形成两个旋涡,分布在旋涡上的测点流速较小,而分布在主流上的测点流速较大。为了更直观地比较数值模拟和模型试验的结果,图8给出休息池数值模拟的结果。
对比图7和图8可以发现,弯道用矩形平面休息池形式,最大流速出现在竖缝跌水末端,这也验证了前面试验的结论。模型试验增加“L”形挡板而改变了主流从竖缝出来后的行进方向,不是贴壁而是向休息池中间运动,这有利于高流速主流的分散,从而降低水流流速,更适于鱼类的洄游。
5 结 论
(1)结合鱼类游动特点来看,矩形结构的弯道设置有效降低主流区和竖缝处流速,为鱼类休息提供更多的低流速区。

图4 圆弧形结构鱼道不同水深的流速等值线

图6 弯道矩形结构形式模型试验

图5 矩形结构鱼道不同水深的流速等值线

图8 数值模拟休息池流速等值线(m/s)

图7 休息池流速矢量图(m/s)
(2)数值模拟的结果显示,圆弧弯道休息池进口处的最大流速能达到1.35m/s,矩形弯道休息池进口处的最大流速为1.20m/s。由于圆弧形结构利于水流过流的特性,水流在鱼道中所受阻力较小,故水流轨迹平顺,流速也整体偏大;矩形弯道结构整体流速相对较小,更利于鱼类洄游时的暂时休息。
(3)物理模型试验结果也验证了矩形弯道休息池布置的优势,并进一步说明了“L”形挡板在流速控制上的优点。
参考文献:
[1] 华东水利学院主编.水工设计手册第6册.泄水与过坝建筑物[M].北京: 水利电力出版社,1982.
[2] 王兴勇, 郭军.国内外鱼道研究与建设[J].中国水利水电科学研究院学报, 2005,3(3):222-226.
[3] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京,清华大学出版社,2004.

