混凝土坝表面温度裂缝计算

吴一匡

(浙江水利水电专科学校，浙江 杭州 310018)

1 坝表面裂缝概况

混凝土坝发生表面裂缝的主要原因，是干缩、年气温变化及寒潮的作用。

贵州省普定碾压混凝土拱坝，坝高74m，发现裂缝49条，裂缝宽度0.1～0.5mm，裂缝长2.5～35m；河北省温泉堡拱坝，高48m，发现3条垂直裂缝，深10～25cm，宽0.1～1mm；安徽省丰乐拱坝，高54m，下游面发现表面裂缝20条，长3～30m，最大缝深214cm，最大缝宽0.4mm；三峡大坝左岸坝段中间部位，发现表面裂缝80多条,缝最长的20～30m，裂缝深度50～100cm,裂缝宽度0.1～0.3mm。

南非Knelpoort坝，高50m，Wolwends拱坝，高70m,二坝产生贯通上、下游裂缝，最大缝宽2～3mm，漏水量2～3.5L/s。

2 年气温变化下的温度场

设x座标o点在半大体积混凝土表面，以年平均气温为温度坐标T的0点，年最高或最低的日气温与年平均气温之差为T0，则气温T(t)=T0cos(wt)，t是时间，w是频率，定解问题是：

(1)

T(x,0) = 0 =T(∞,t)

(2)

(3)

式中a——混凝土导温系数；

δ——第三类边界空气层流层厚度。

Laplace变换：

微分方程(1)，在边界条件(2)下变换为F(x，p)=cexp(-pt)dt，把条件(3)变换确定系数c后，得到：

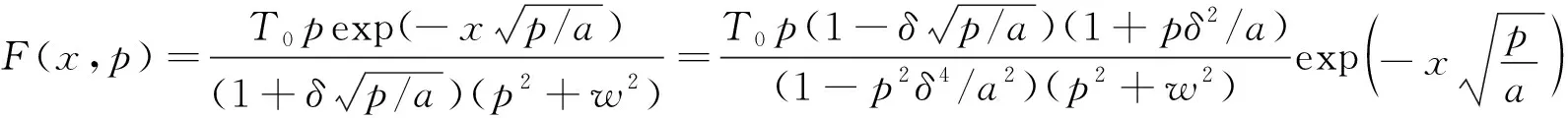
逆变换，分母=0，得两组根：p=±a/δ2，p=±iw，

把以上两组根代入，得到温度是：

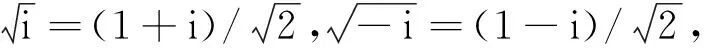
代入上式得：

把复指数函数转变为三角函数，得到大体积的温度场是：

(4)

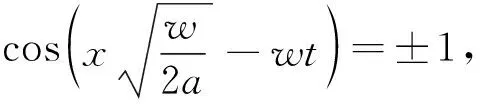
(5)

3 表面裂缝深度及宽度

按S.Timoshenko弹性力学，混凝土最大应力：

(6)

式中E——混凝土弹性模量；

α——线性膨胀系数；

kp——应力松弛系数；

μ——泊松比。

按上式算出深度x处的σ，当σ等于混凝土允许抗拉强度时,则x就是裂缝深度。造成裂缝的温度场边界形状，是底宽2xm、高度xm的三角形，因此:

裂缝宽度：Δy=2xα[T(0)-T(x)]

(7)

式中T(0)——坝表面x=0处的温度；

T(x)——裂缝深度x处的温度。

[例题]年最高或最低气温与年平均气温之差T0=±25℃，混凝土导温系数a=0.096m2/d，弹性模量E=0.27×105MPa，膨胀系数a=0.6×10-5/℃，泊松比μ=1/6，应力松弛系数kp=0.61，150号混凝土允许抗拉强度σ=1.47MPa，空气层流边层δ=0.11m，试计算裂缝宽度和深度？

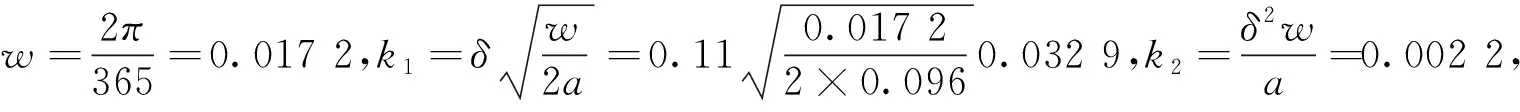
代入式(5)得温度T(x)=±24.2exp(-0.299x)，按此式算出的年最大温度见表1。

按式(6)，最大拉应力：

按此式算出的拉应力见表1。

150号混凝土允许抗拉强度σ=1.47MPa，从表1查得裂缝深度x=2.24m。按式(7)计算裂缝宽度:

Δy=4 480×0.6×10-5(-24.2+12.4)=-0.3mm

以上计算结果与三峡大坝及丰乐坝等的实测资料接近。

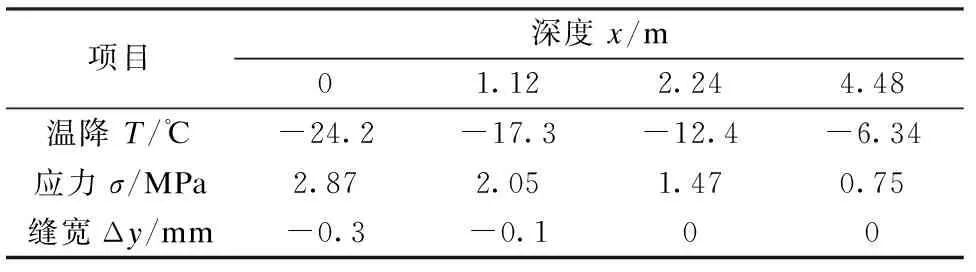
表1 表面温度裂缝计算