RC振荡电路特性EWB仿真分析——以文氏桥振荡电路为例
许昌职业技术学院 机电工程系 李亚男
一、RC振荡电路简介
采用RC 选频网络构成的振荡电路称为RC 振荡电路,它适用于低频振荡,一般用于产生1 Hz~1 MHz的低频信号。因为对于RC 振荡电路来说,增大电阻R 即可降低振荡频率,而增大电阻是无需增加成本的。从结构上来看,正弦波产生电路应包括放大电路、正反馈网络、选频网络和稳幅电路,这些是必要条件,其中的选频网络可以设置在放大电路中,也可设置在正反馈网络中,甚至可以设置在放大电路的负反馈网络中。但这不是随意的,要保证对于选频网络的中心频率而言,能够满足幅度条件和相位条件,正弦波振荡器是一种基本的电子电路,电子技术试验中经常使用的低频信号振荡器就是一种正弦波振荡电路.无论对于哪种振荡电路,用传统方法精确分析起振、振幅、振荡频率的大小都是十分困难的,而用EWB 软件则可进行仿真分析.本文,笔者以文氏桥振荡电路为例,采用EWB 软件对其正弦波振荡器的起振过程及各参数对频率和振幅的影响进行仿真分析,以期对同行有所参考。
二、特性分析
理想运算放大器具有虚断特牲,为克服RC移相振荡器的缺点,常采用RC 串并联电路作为选频反馈网络的正弦振荡电路,也称为文氏桥振荡电路,其结构如图1所示。

图1 文氏桥振荡电路结构
它由两级共射电路构成的同相放大器和RC 串并联反馈网络组成。由于φA=0,这就要求RC串并联反馈网络对某一频率的相移φF=2nπ,才能满足振荡的相位平衡条件。
由图1可知,当f0=1/(2πRC),F 的模最大,且|F|=1/3,φF=0;当f>f0时,|F|减小,且φF≠0,f0=1/(2πRC),由|AF|>1 知起振条件为|A|>1,这表明RC 串并联网络具有选频特性,因此图1电路满足振荡的相位平衡条件。如果同时满足振荡的幅度平衡条件,就可产生自激振荡,振荡频率f=f0=1/(2πRC)=1.592 kHz。
三、优缺点分析
文氏桥振荡器不仅振荡较稳定,波形良好,而且振荡频率在较宽的范围内能方便地连续调节,其相位φA+φF=2nπ(n=0,1,2,…)。在设计振荡器时首先需要考虑相移。从理论上讲,利用文氏电路产生正弦波非常简便,然而从实际情况考虑实际意义不大,因为电阻的精度很好控制,而电容容值的精度很难控制,即使是精度为±20%的电容成本也很高。比较明智的办法是首先考虑电容器精度对电桥性能的影响,然后找到一种低成本的弥补办法。
四、仿真结果
为了稳定输出电压的幅值,一般应在电路中加入非线性环节。非线性环节的作用必须保证开环放大倍数k稳定在3,当k<3 时,应加大RF或减小R,而当遇k>3 时,应减小RF或加大R。经过调节电阻R1来改变起振情况。振荡器的慢速起振过程如图1所示,快速起振过程如图2所示。
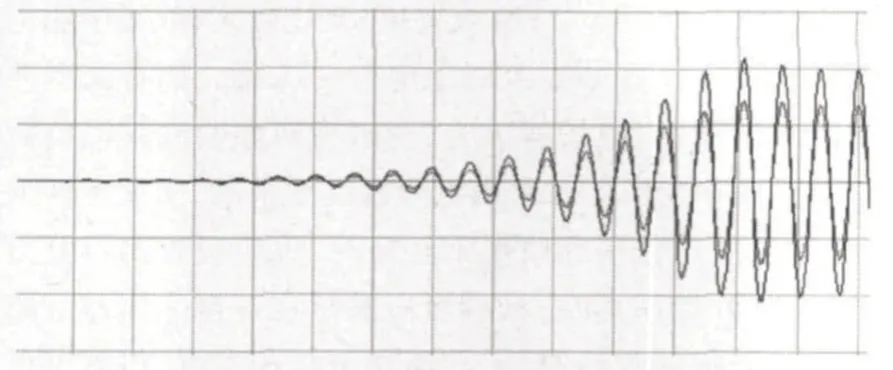
图2 慢速起振过程
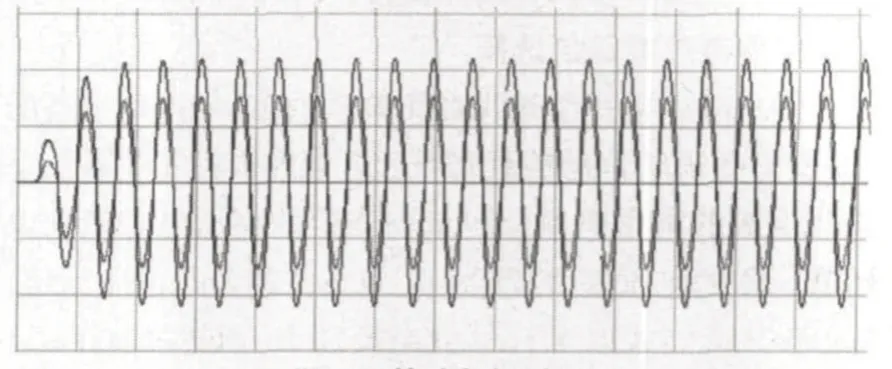
图3 快速起振过程
五、结果分析
1.当f=f0时,反馈信号与原输入信号同相位,满足相位条件;反馈电路输出电压只有反馈电路输入电压的且最大。因此,集成运放组成f0的放大电路中RF略大于2R1时就能满足振幅条件,从而产生振荡,振荡频率为f0=1/(2πRC)。若RF<2R1,电路不能起振;若RF>2R1输出电压Uo的波形会产生接近方波失真。
2.当f≠f0时,反馈电路输出信号与输入信号的相位不同相,无正弦波信号电压输出。
3.为产生振荡,f=f0信号电压必须有一个从微弱开始逐渐增大,直至稳定的过程。实用中,常采用改变RF/R1来实现稳幅。例如,选择负温度系数的热敏电阻作反馈电阻RF,当输出电压增加使RF的功耗增大,它的温度上升,其负温度系数使它的阻值下降,于是闭环电压放大倍数减小,达到稳幅目的。同理,也可选择正温度系数的热敏电阻作电阻R1,实现稳幅。RC文氏桥振荡电路结构简单,起振容易,频率调节方便,适用于低频振荡场合,最高振荡频率一般为10~100 kHz。

