大型立式储罐风致静力屈曲分析

魏化中 张占武 丁克勤 舒安庆

（1.武汉工程大学机电工程学院 2.中国特种设备检测研究院)

大型立式储罐风致静力屈曲分析

魏化中*1张占武1丁克勤2舒安庆1

（1.武汉工程大学机电工程学院 2.中国特种设备检测研究院)

利用ANSYS特征值屈曲分析对四种径高比 (D/H)的浮顶油罐进行风压局部侧向失稳研究。以10万m3储罐为例，考虑储罐的圆度缺陷，进行了非线性屈曲分析和抗风设计。结果表明：大型储罐随着径高比的增加局部屈曲临界压力下降，其大小主要取决于上层圈板的厚度；进行抗风设计对提高储罐临界压力作用明显；随着圆度的增加，屈曲临界压力随之下降；非线性屈曲分析比特征值屈曲分析对圆度缺陷敏感度更高。

大型储罐 风压失稳 特征值屈曲分析 圆度 压力容器

0 前言

目前国内已有数百台在役的10万m3及以上大型油罐。储罐的安全运行关系重大，一旦发生泄漏或爆炸就有可能引发严重的人员伤亡和造成重大的经济损失。储罐的失效模式可分为腐蚀、材料退化、开裂和严重变形等。在地震或者风载荷下发生屈曲属于结构变形。部分结构变形可以修复，而另外一些严重变形不能修复的储罐则宣布报废。在地震波或者风压作用下，储罐有可能发生轴向失稳或局部侧向失稳。本文利用ANSYS屈曲分析讨论了储罐在风压下侧向失稳问题。

1 储罐的风致静力屈曲研究概述

储罐属于薄壁短圆筒构件，其在风载荷作用下的失稳属于侧向失稳。充满液体的罐子因为罐壁受到盛装介质垂直于筒壁的静压力对外压的平衡作用，一般不会发生侧向失稳。而储罐在日常运行过程中存在空罐状态。对于放空液体的空罐，或者在安装施工过程中未安装抗风圈和加强圈的罐体，有可能发生侧向失稳。

在均匀外压作用下，储罐的侧向失稳临界压力的计算公式可采用中科院力学研究所[1]的推荐公式：

式中pcr——罐壁筒体的临界压力，Pa；

K——安全系数；

E——弹性模量，Pa；

Kcr——临界压力系数；

δm——去除强度计算所余金属的指数函数罐壁平均厚度,mm；

R——储罐半径，m；

L——罐壁的计算高度，m。

或者采用SH 3046—1992[2]中储罐的临界压力计算公式：

式中pcr——罐壁筒体的临界压力，Pa；

D——储罐内径，m；

HE——抗风圈以下的罐体总当量高度，m；δmin——圈板的最小厚度，mm。

前者是把阶梯状的变截面罐壁按截面积相等的原则简化为壁厚按指数方程连续变化的罐壁，把求解阶梯状截面罐壁的风力稳定问题简化成求解按指数变厚度的圆柱壳体在均匀侧压下的临界压力问题。后者是根据薄壁短圆筒在外压作用下的临界压力公式得到的，并把筒体高度用当量高度表示。

由于风压分布是不均匀的，而且罐壁截面是阶梯状变厚度的，用上述两个近似公式计算出来的屈曲临界压力存在较大误差。采用有限元方法对储罐进行屈曲分析，可以模拟罐壁的变厚度的作用，风压也可以考虑周向和竖向压力变化，能够得到较为准确的屈曲临界压力。

2 储罐静力风致屈曲建模和计算

2.1 罐壁风压分布

罐壁周围的风压分布不均匀，是沿周向和高度变化的。风压的周向分布，不同的资料取值不尽相同。GB 50009—2011《建筑结构荷载规范》[3]中给出了一系列计算风压用体形系数的离散值。国外的许多学者采用三角函数对风洞试验进行了拟合。以下给出一种拟合得到的风压分布公式[4]：

式中qw——罐壁外侧风压分布值，kN/m2;

cm——Fourier系数；

mφ——周向展开角度。

对于圆柱面的风压分布，除迎风面小部分区域存在正压作用外,大部分区域是负压作用。在风速较低而场地粗糙度较大时,还观测到全表面均为负压的情况[5]（见图1）。本文的风压分布采用Pircher建立的罐壁周向风压系数公式，在高度方向上认为风压分布相同[4]：

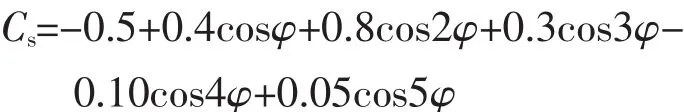
图1 罐壁风压分布

2.2 储罐模型建立

本文分析的四种径高比 （D/H）的储罐的几何参数如表1所示。先按未进行抗风设计的裸罐进行计算。罐壁按照实际厚度建模，单元选用4节点每个节点6自由度的shell 181单元，shell 181单元能够很好地模拟线性、大转角和大变形的非线性问题。 泊松比 μ=0.3， 杨氏弹性模量 E=2.06×105MPa。风压加载通过定义函数的方式加到储罐的外表面上。也可以通过表参数法定义三维实数数组，通过线性插值法来进行加载。实际上通过函数加载的方法最终也转化为通过数组进行加载。储罐下部的边界条件可以取为锚固，最下层的一圈节点施加全约束。由于储罐下部锚固，底板对整个结构的刚度矩阵没有贡献，所以有限元模型中可以不考虑底板的影响[6]。 储罐的风压失稳容易发生在空罐或者卸载状态，故建模时不考虑储液的影响。基于以上分析，建立了四种不同高径比储罐的有限元模型。

2.3 储罐风致静力屈曲有限元分析

2.3.1 特征值屈曲分析

经典的屈曲分析是采用特征值屈曲分析法，它适用于对一个理想弹性结构的理论屈曲强度 (歧点)进行预测，主要是使用特征值公式计算造成结构负刚度的应力刚度阵的比例因子。

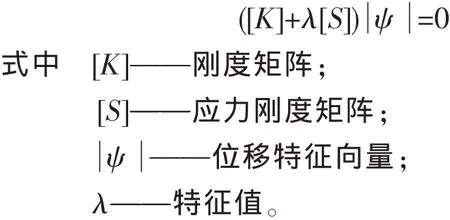
特征值屈曲分析属于结构线性分析，用于预测理想线弹性的理论屈曲强度。一般认为，特征值屈曲分析的结果是屈曲临界载荷的上限。不过一些文献也指出这并不是绝对的[7]。 可以作为预估的临界荷载值，特征值屈曲分析的屈曲模态形状可以作为初始缺陷应用于非线性分析。通过特征值屈曲分析求解屈曲临界压力的步骤是：在基本的静力学求解之后，重新进入求解器进行屈曲分析。打开预应力选项（屈曲分析要考虑结构的几何刚度），选择迭代方法 （ANSYS提供了两种求解特征值的迭代方法，即子空间法和兰索斯法，前一种求解精度较高，后

表2 三种方法计算屈曲临界载荷结果比较

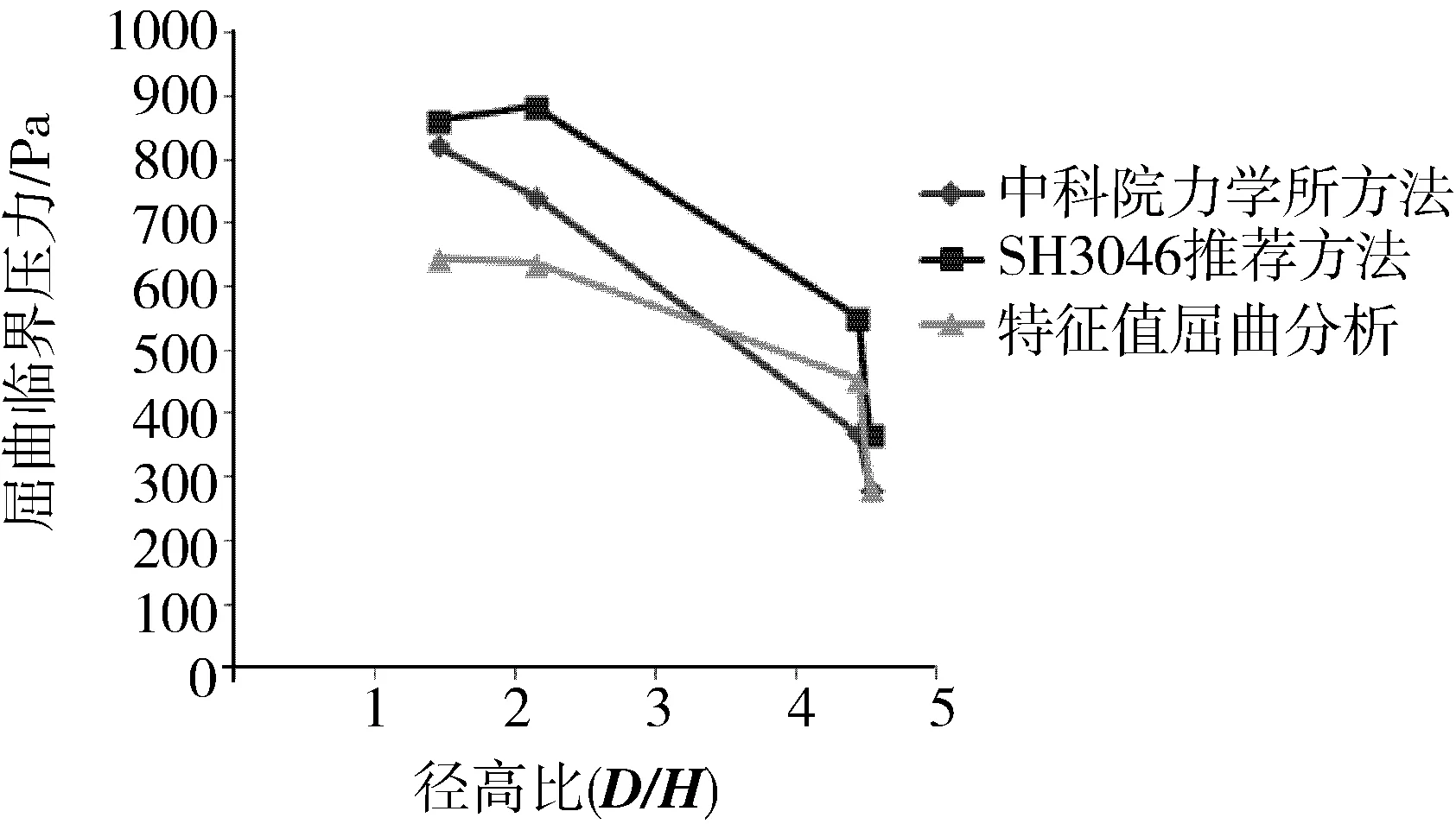
图2 三种方法计算屈曲临界载荷结果比较

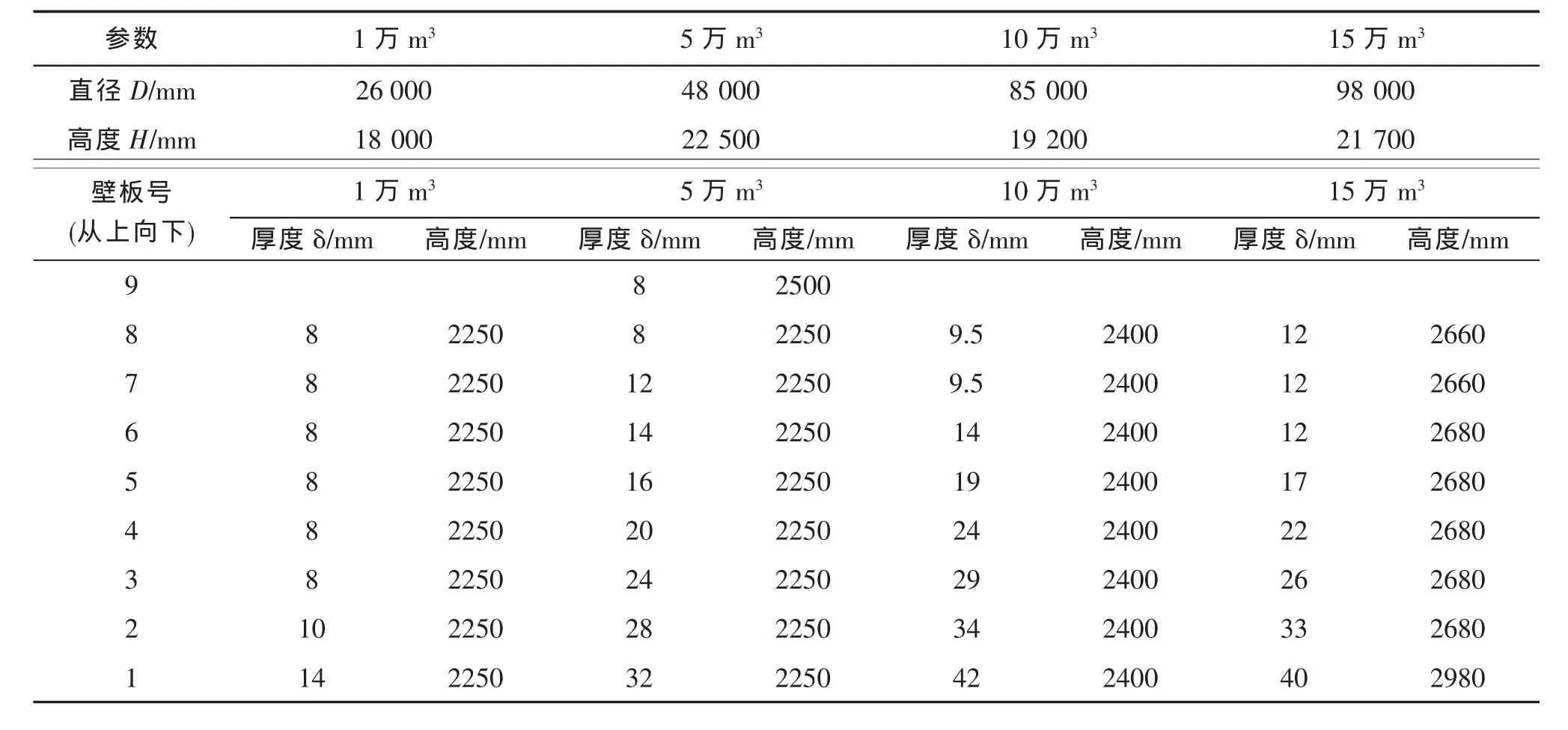
表1 四种不同容积油罐壁板参数

本文计算的4个算例随着D/H的增大屈曲临界压力有下降的趋势，这和等厚度圆筒均匀外压失稳公式中分析得到的变化趋势是相反的。这是由于储罐的各层壁板的厚度不同，在上层圈板首先发生了屈曲。从计算结果中看到，把储罐进行等厚处理按均匀外压失稳来计算的前两种方法得到的屈曲临界压力要偏大。对于大型储罐来讲，底层圈板和顶层圈板的厚度差距有的达到30 mm以上，采用等厚处理不能反应实际的局部屈曲。从屈曲模态形状上看，1万m3、5万m3、10万m3和15万m3的储罐失稳波数 （见图3）分别为2、3、5、5。由图3可以看出，屈曲发生在迎风子午线左右大约30°的区域内，这与空罐容易在迎风区域60°范围内发生凹瘪的事实一致。在求得屈曲临界压力后，对应的风速可以根据风速风压之间满足的伯努利方程求出。针对15万m3储罐的屈曲临界压力281.3 Pa，求得对应的风速为21.2 m/s，属9级风的范围，陆地上并不少见。1万m3储罐屈曲临界压力对应的风速为32 m/s，属11级风的范围，陆上虽然非常少见，但是一旦出现就会造成重大损毁。因此有必要对储罐进行抗风设计。

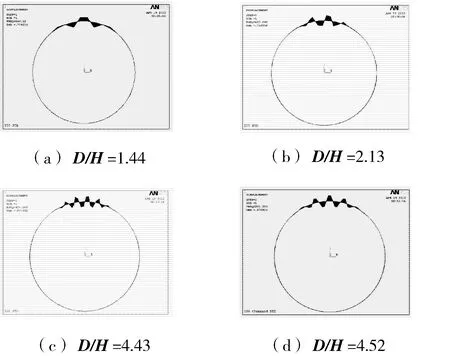
图3 不同径高比储罐一阶屈曲模态形状比较

2.3.2 非线性屈曲分析

非线性屈曲分析是在选定大变形效应的情况下所做的一种静力分析。非线性屈曲分析可以考虑几何非线性、材料非线性、大变形和初始缺陷等问题。ANSYS中载荷控制、位移控制和弧长法是用于求解非线性静态屈曲问题的三个技术。本文采用弧长法求解，弧长法求解的步骤是在特征值屈曲分析的基础上施加初始几何缺陷或初始扰动进行非线性屈曲分析，最后从荷载-位移曲线上得到屈曲临界压力 （见图4）。结构的初始缺陷包括厚度偏差、圆度等。本文选取10万m3裸罐0%、4%、8%、12%、16%和20%六种圆度缺陷进行特征值屈曲分析和考虑几何非线性的非线性屈曲分析，并将计算结果进行了对比 （见图5）。从计算结果可以看出，随着圆度的增大，屈曲临界压力随之下降；和特征值屈曲分析相比，非线性屈曲分析得到相对保守的结果且对圆度缺陷更加敏感。

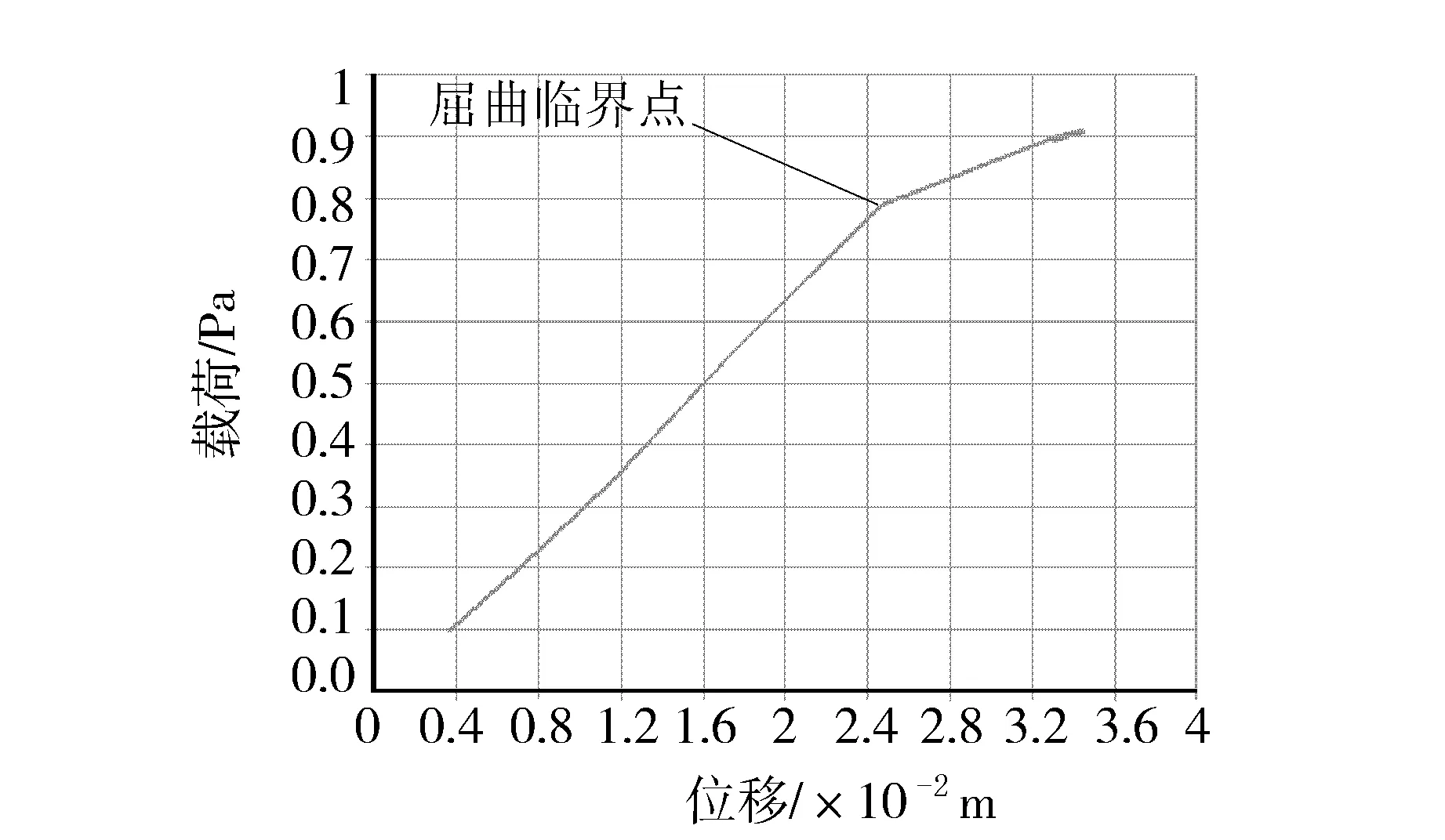
图4 4%圆度缺陷下节点17991荷载-位移曲线

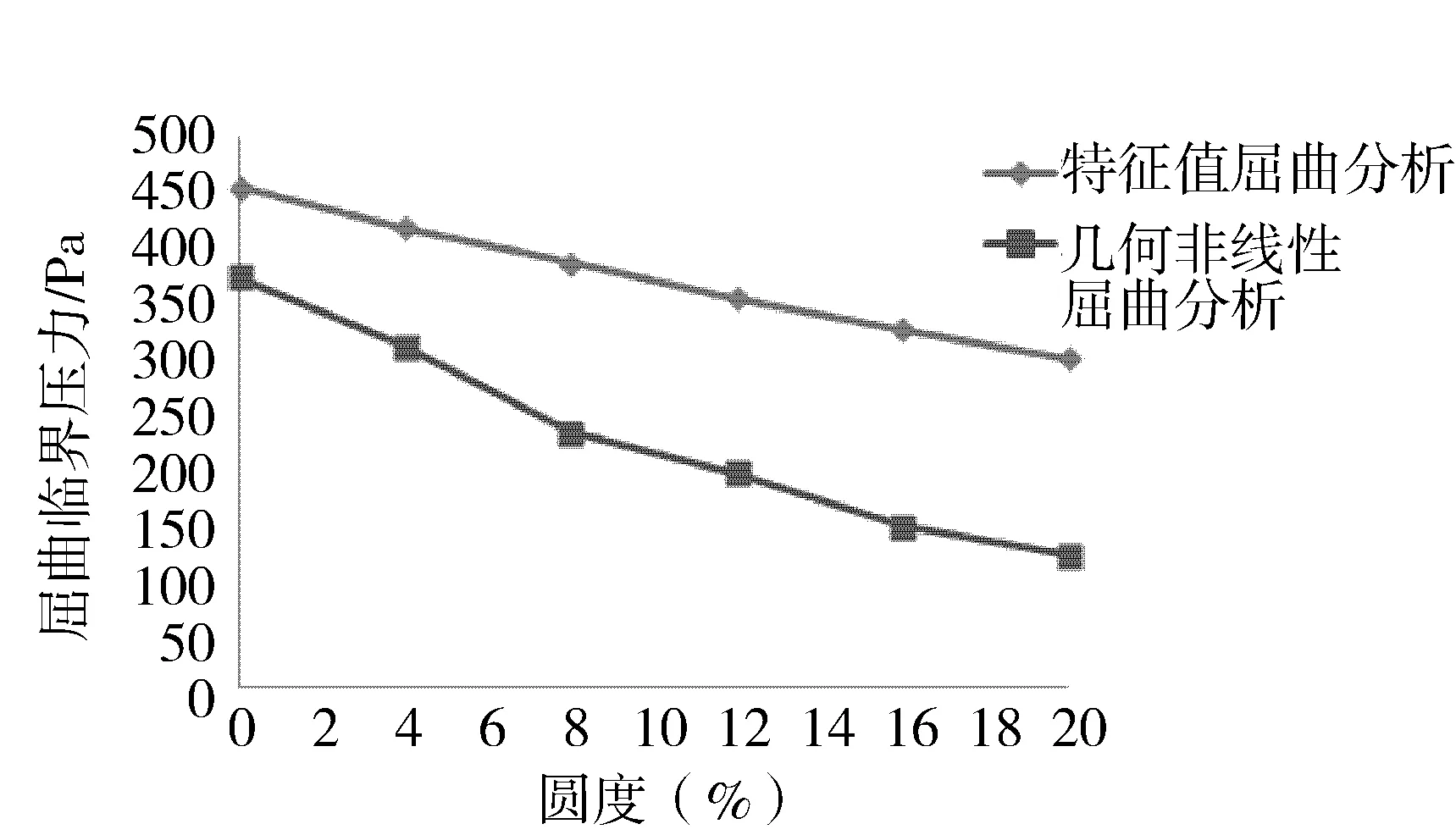
图5 不同圆度缺陷下的临界压力比较

3 储罐的抗风设计

本文选取10万m3的储罐进行了抗风设计，具体按照文献[8]的要求进行设计计算。储罐的抗风设计包括包边角钢、顶部抗风圈和中间加强圈设计。顶部抗风圈设计包括抗风圈最小截面系数的计算、抗风圈结构的选择。对于浮顶储罐，抗风圈一般安装在距顶部包边角钢1 m的位置。是否需要设置加强圈取决于设计风压p0和屈曲临界压力pcr的大小比较。对于浮顶储罐，罐壁的设计外压可按下式计算:

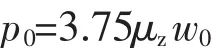
式中 μz——风压高度变化系数；

w0——基本风压，kN/m2。

本文研究的10万m3浮顶储罐处于沿海地区，风压高度变化系数取海拔40 m、A类地区的数值，基本风压值取大连地区的基本风压值。求得设计风压p0=4212 N/m2。浮顶储罐包边角钢的尺寸取L75 mm×6 mm。计算得到抗风圈的最小截面系数为7484 cm3。计算得到储罐的设计风压大于其屈曲临界压力p0＞pcr，须设置加强圈。加强圈多采用角钢，通常安装在罐壁外部。加强圈数量和位置的计算采用SH 3046—1992推荐的方法。最后求得加强圈的数量为2个。一个距顶部抗风圈2.644 m，位于从上向下第二层圈板。另一个距顶部抗风圈5.456 m，位于第三层圈板。图6给出了抗风圈和加强圈的安装位置和结构尺寸。

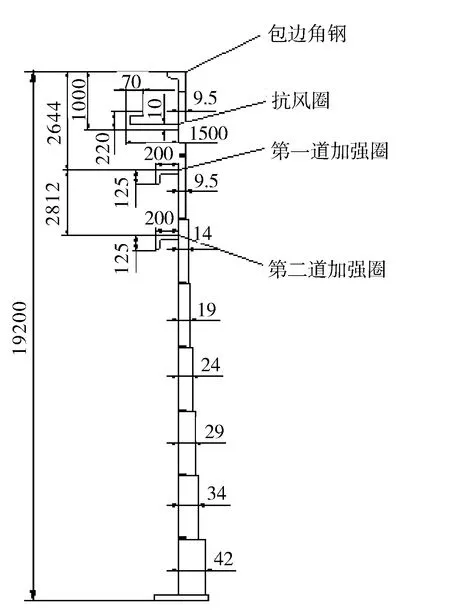
图6 抗风圈、加强圈安装位置

加装抗风圈和加强圈之后，建立了相应的几何模型 (见图7)和有限元模型进行求解，抗风圈和加强圈仍选用shell 181单元。特征值屈曲分析求得10万m3储罐的屈曲临界压力为7128 Pa。储罐的一阶屈曲模态形状如图8所示。进行抗风设计之后的加劲罐的屈曲临界压力是裸罐的将近16倍，对应风速为107 m/s，这一风速在自然界中几乎不存在。抗风圈和加强圈以上的圈板不发生屈曲。可见加装抗风圈和加强圈后屈曲临界压力显著提高。

4 小结

本文用ANSYS特征值屈曲分析方法研究了四种径高比不同的储罐风压下的局部侧向失稳问题，以其中一10万m3储罐为例进行了抗风设计，比较了裸罐和加劲罐屈曲临界压力的变化。考虑圆度初始缺陷和几何非线性，采用弧长法对10万m3储罐进行了非线性屈曲分析。结果表明，大型储罐随着径高比的增加局部屈曲临界压力下降，局部屈曲临界压力大小主要取决于上层圈板的厚度；进行抗风设计对提高储罐临界压力作用明显；随着圆度的增加，屈曲临界压力随之下降;非线性屈曲分析较之特征值屈曲分析对圆度缺陷更加敏感。

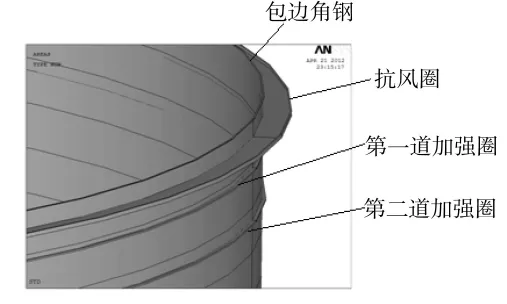
图7 加劲罐的几何模型

图8 加劲罐的一阶屈曲模态形状

[1]徐英,杨一凡,朱萍.球罐和大型储罐 [M].北京:化学工业出版社,2005.

[2]SH 3046—1992.石油化工立式圆筒形钢制焊接储罐设计规范 [S].

[3]GB 50009—2011.建筑结构荷载规范 [S].

[4]穆春生.LNG储罐在静风和内压作用下的受力性能分析 [D].大庆：东北石油大学,2011.

[5]李元齐,Tamura Yukio,沈祖炎.柱面壳体表面风压分布特性风洞试验研究 [J].同济大学学报 （自然科学版），2006,36(11):1457-1463.

[6]马昌恒.基于小波分析的风场模拟及大型储罐风致屈曲初步研究 [D].大庆：大庆石油学院，2007.

[7]韩庆华,金辉,艾军，等.工程结构整体屈曲的临界荷载分析 [J].天津大学学报,2005,38(12):1051-1057.

[8]GB 50341—2003.立式圆筒形钢制焊接油罐设计规范[S].

Buckling Analysis of Large Vertical Type Storage Tank by Static Wind Load

Wei Huazhong Zhang Zhanwu Ding Keqin Shu Anqing

This paper analyzed the local wind load lateral buckling problems of floating roof tanks with four different diameter height ratios(D/H)using ANSYS eigenvalue buckling analysis.Considering the ellipticity defect wind force proofing design and nonlinear buckling analysis were proceeded taking the 100,000 m3storge tank as an example.The results showed that the buckling critical pressure fell along with the increase of diameter height ratio,and it mainly depended on the thickness of upper girth sheets.It's obvious to enhance the critical pressure by force proofing design.The buckling critical pressure became small following the ellipticity's increase.Nonliear buckling analysis was more sensitive to ellipticity defect compared to eigenvalue buckling analysis.

Large storage tank;Wind load unstability;Eigenvalue buckling analysis;Ellipticity； Pressure vessel

TQ 053.2

*魏化中，男，1955年生，副教授。武汉市，430073。

2012-05-28）