基于ANSYS的球形封头压力容器的可靠性分析

许安俊 孙 斌

（扬州联合化工机械有限公司)（江苏省特种设备安全监督检验研究院扬州分院）

基于ANSYS的球形封头压力容器的可靠性分析

许安俊*孙 斌

（扬州联合化工机械有限公司)（江苏省特种设备安全监督检验研究院扬州分院）

为了及时、准确地对压力容器进行可靠性评估，将ANSYS和蒙特卡罗相结合方法引入压力容器模型的计算中。以概率论为基础，用此方法对建立的模型进行500次随机抽样分析，求出在一定置信度下的可靠度曲线；并对输出随机变量的灵敏度和抽样过程进行了分析，求得对结果影响最大的因素是屈服强度。结果表明，该模型可以有效地反映压力容器的实际情况，为其结构可靠性分析提供参考。

压力容器 球形封头 可靠度 ANSYS 蒙特卡罗

随着现代工业设备向着高参数方向发展，对压力容器设计提出了更高的要求，不仅要求其效率高、成本低，而且要求在各种工况下具有足够的安全可靠性。为了保证设备的安全经济运行，对在役压力容器性能的可靠性进行定期评估显得意义重要。压力容器的设计参数如压力、强度、温度、几何尺寸等都具有一定程度的不确定性和分散性。采用确定性方法求出的结果常常和实际状态相差较远，因此目前多采用概率设计方法。本文采用有限元和蒙特卡罗相结合方法，对压力容器结构进行可靠性和灵敏度分析，并对结果进行讨论。

1 基于ANSYS的可靠性分析功能

目前解决复杂结构可靠性问题的常用方法有蒙特卡罗法、响应面法等。蒙特卡罗法是一种用数值模拟来解决与随机变量有关的实际工程问题的方法。对随机变量的数值模拟相当于一种 “试验”，所以蒙特卡罗法又称为统计试验法。蒙特卡罗法适用面广，并且只要建模准确，模拟次数足够，所得结果是可信的。蒙特卡罗模拟是目前可靠度分析结果正确性验证的惟一手段。响应面法是近几年发展起来的进行可靠性分析的另一种有效方法，其思想是通过系列确定性试验拟合一个响应面来模拟真实的极限状态，从而进行可靠性分析。蒙特卡罗法中所需循环次数与变量个数无关，只取决于所输出结果的类型及分散程度。响应面法中模拟循环次数取决于输入变量的个数。对屈曲、接触以及理想弹塑性分析等问题，输入变量的细微变化可能导致输出变量突变，这时响应面法不适用。

以ANSYS进行可靠性分析的一般过程包括：（1）定义输入变量及输入变量之间的相关系数，确定各输入变量服从的分布类型、分布函数及其参数； （2）指定输出结果变量； （3）选择分析工具和方法； （4）执行可靠性分析循环。

2 可靠性的相关理论 [3]

结构的可靠度是指结构在规定的时间内、规定的条件下 （正常使用极限状态和承载能力极限状态）完成预定功能的概率。

若结构的基本变量由X1，X2，…，Xn组成，且结构功能Z为基本变量的函数， 则结构功能函数 (极限状态函数)可表示为：

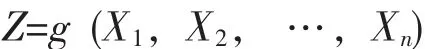
在概率极限状态设计理论中，极限状态方程为：

通常在结构设计中,基本变量X1，X2， …，Xn为随机变量，如果把基本变量归结为结构抗力R和载荷效应S两大类，则结构功能函数可简化为：

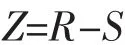
所以在概率极限状态的结构设计中，必须满足下列条件，即：

由可靠性理论可知，求一个结构的可靠度就是求极限状态函数g(X)≥0的概率，所以，利用ANSYS概率分析功能计算g(X)≥0的概率，就得到了结构的可靠度。

3 具体实例

3.1 问题描述

某高压容器设计压力p=16 MPa，设计温度200℃，材料为16MnR；筒体内径R1=775 mm，筒体壁厚t1=100 mm；封头内径R2=800 mm，封头壁厚t2=48 mm；筒体削边长度L=95 mm。试分析该高压容器的使用可靠性。

3.2 建立模型并求解

本课题主要进行筒体与封头之间应力的可靠性分析，算例中只考虑机械应力，忽略热应力。建立简化的有限元计算模型 （见图 1），省略压力容器的其他结构 （如开孔接管等）进行应力分析。有限元模型采用PLANE 82单元，并设定轴对称选项，建立1/4轴对称分析模型。筒体下端各节点约束轴向位移，椭圆封头对称面各节点约束水平方向位移，内壁施加均匀压力面载荷。网格的划分与载荷施加如图2所示。

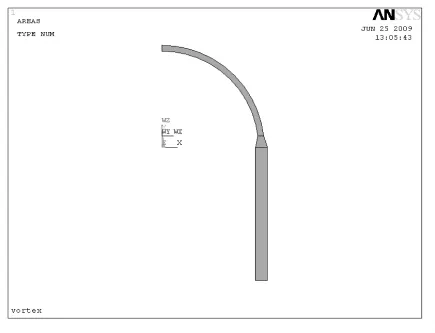
图1 有限元模型

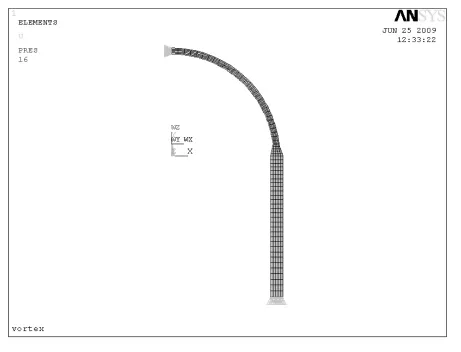
图2 网格划分与加载

3.3 可靠性分析

本例采用ANSYS有限元程序的概率设计功能PDS，选用蒙特卡罗法进行压力容器的可靠性分析。以容器的壁厚、压力载荷、弹性模量作为随机输入变量，材料的屈服极限为随机输出变量，计算结构的可靠度。在该结构的可靠性分析中，假设材料的几何尺寸、载荷遵循正态分布。随机变量及其分布如表1所示。

由压力容器的强度理论可知，压力容器使用过程中不允许应力超过屈服强度的事件发生，如果应力超过屈服强度则认为失效。失效准则为：

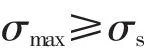
式中σmax——容器使用过程中出现的最大应力;

σs——材料的屈服强度。

极限状态方程为：

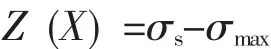
Z(X)≤0为失效状态。其中X为式中的所有不确定量组成的向量。

本例中求压力容器的可靠度就是求Z(X)≤0的概率。

3.4 结果分析由ANSYS有限元概率分析的计算结果可知：（1）在置信度为95%的情况下，Z＜0的概率平均为8.88%，即说明容器的可靠度为91.12%。

（2）由图3可知，Z＞0的分布占主要空间，其概率分布对应于上述置信度95%情况下所得的结果。

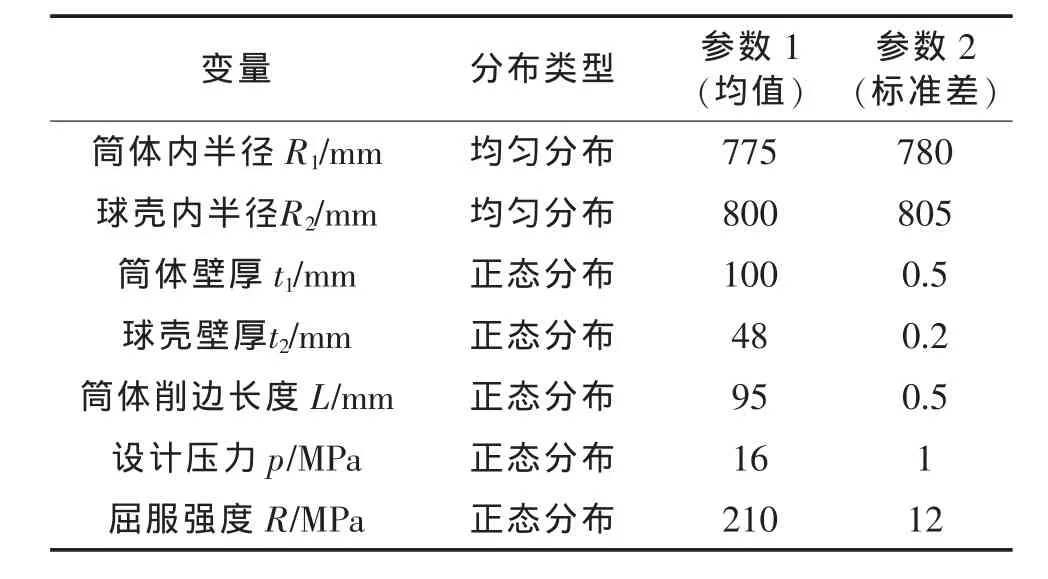
表1 随机变量概率分布类型及参数

图3 Z在置信度95%情形下的分布图

（3）抽样过程显示 （见图4），输出变量的平均值收敛，表明模拟的次数足够。

图4 MAXSTR抽样过程显示

（4）输出变量MAXSTR （最大应力）灵敏度分析如图5所示，从结果中可以看出，p、R1、R2对结果的影响比较大，其余的参数影响甚小。当p值增大时，结构的等效应力增大，强度的可靠性降低。

图5 MAXSTR灵敏度分析

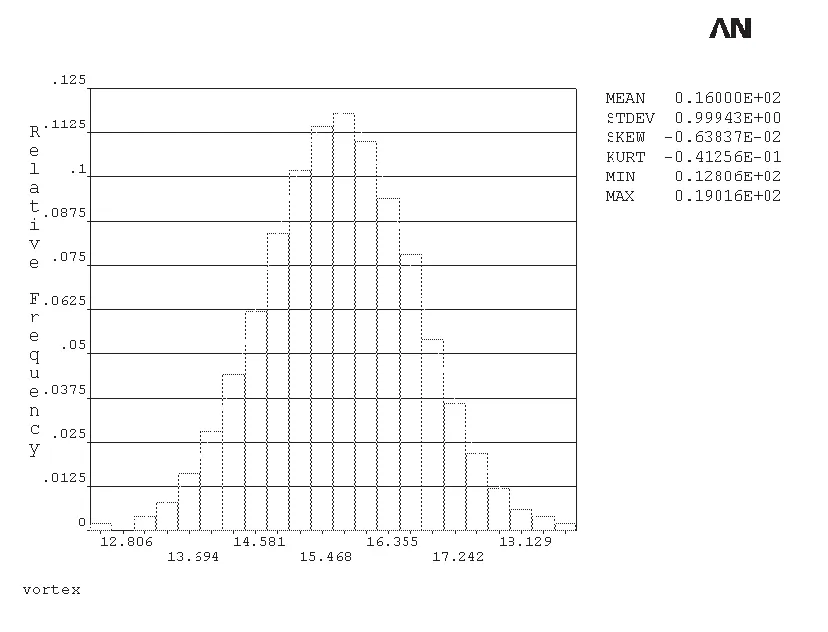
图6 p取值分布柱状图

（5）p是影响失效的最主要因素，通过其取值柱状图（图6）可见，柱状图靠近函数曲线，且不存在较大的间隙和跳跃，这也表明模拟次数已经足够。

4 结语

在对压力容器计算结果进行分析时，对算例的可靠度影响较大的因素是工作压力、筒体内半径和球壳内半径，影响较小的其它因素可忽略不计。但在实际工况中，各因素并非完全独立的，存在着相关性，所以有必要在此基础上进行深入的研究和探讨。

在对压力容器模型进行可靠性分析时，采用了蒙特卡罗和ANSYS相结合的方法。此方法和程序都很简单，便于接受和推广。从计算过程和结果来看，此方法提高了计算的准确性，减少了工作量，结果更接近于工程实际。由此可见，概率有限元数值模拟法是压力容器安全评估的有力工具。

[1]何水清，王善.结构可靠性分析与设计 [M].北京：国防工业出版社，1993： 50-99.

[2]余伟炜,高炳军.ANSYS在机械与化工装备中的应用[M].北京：中国水利水电出版社,2007：341-372.

[3]王伟.基于ANSYS的盲盖板可靠性分析 [J].石油化工设备技术，2007，28(2)：9-10.

[4]王亦凌,龚翠元,李建明.基于ANSYS的球形压力容器的结构强度可靠性分析 [J].化工装备技术,2007，28(4)：34-36.

[5]叶勇,郝艳华,张昌汉.基于ANSYS的结构可靠性分析[J].机械工程与自动化， 2004（6）：63-65.

[6]王金龙.基于蒙特卡罗法的压力容器可靠性风险分析[J].潍坊学院学报，2008，8(4)：5-8.

[7]王明强,朱彤.应用ANSYS概率有限元法的连杆结构强度可靠性分析 [J].现代制造工程,2008（3）：54-57.

[8]刘丽芳.压力容器的可靠性分析 [J].湖北化工，1999（5）： 41.

Reliability Analysis of Spherical Head Pressure Vessels Based on ANSYS

Xu Anjun Sun Bin

In order to assess the reliability of pressure vessel timely and accurately,the method which combined ANSYS with Monte Carlo was introduced into calculation of pressure vessel model.Based on probability theory,500 random sampling analyses of the established model were done,the reliability curve under certain confidence level was obtained.The sensitivity of the output random variable and sampling process were analyzed,obtaining that the most influencing factor of the results was yield strength.The results showed that the model could effectively reflect the actual situation of pressure vessel,which could provide reference for structural reliability analysis.

Pressure vessel;Spherical head;Reliability;ANSYS;Monte Carlo

TQ 053.2

*许安俊，男，1974年生，硕士研究生。扬州市，225600。

2011-10-21）