接收函数反演地壳S波速度结构的有效约束方法

彭恒初，胡家富，杨海燕，文丽敏

云南大学地球物理系，昆明 650091

接收函数反演地壳S波速度结构的有效约束方法

彭恒初，胡家富＊，杨海燕，文丽敏

云南大学地球物理系，昆明 650091

本文通过对径向接收函数和垂直向接收函数进行低通滤波，获取了S波视速度随低通滤波参数的变化曲线，然后利用经验关系将它转换成了台站下方的S波速度结构，并以此作为接收函数反演的初始模型.理论数值实验表明：由于初始模型的S波速度值提供了有效的约束，即使Moho面深度并不准确，但反演迭代过程还是快速地向真解逼近.另外，通过给观测波形加入10%的噪声，在保持S波速度不变的情况下，分别对波速比进行5%的正负扰动（即泊松比分别扰动为0.23和0.27），反演结果仍然快速向真解收敛.对保山台记录的远震接收函数反演结果表明：用本文方法反演所得结果与测深结果较为一致.这充分说明只要S波速度值（而非泊松比）能够提供有效的约束，接收函数的反演过程对P波速度的选取并不敏感.

接收函数，反演，初始模型

1 引 言

远震P波接收函数在很大程度上消除了震源时间函数和传播路径的影响，主要由观测台站下方的地壳、上地幔速度界面所产生的Ps转换波及多次反射震相组成，并且对近台站的剪切波速度结构非常敏感［1］.因而，在过去十几年里，用接收函数反演台站下方的S波速度结构是探测壳幔结构的有效方法之一.不过，接收函数反演是一个强非线性问题，反演结果有很强的非惟一性［1］.对于非线性问题，目前主要采用以下两种处理办法，一种是对反演方程进行线性化，将其转变为一个线性反演问题；而另一种就是直接进行非线性反演.

为了有效抑制接收函数反演问题的非惟一性，近年来发展了多种非线性反演方法.其中，一种最常见的方法是利用半空间上覆盖一层的最简单模型，然后基于二维网格进行搜索［2］.这种方法由于比较简单，被广泛用于确定壳幔边界.但是这种最简化的地壳模型忽略了地壳结构本身的复杂性，因此这种近似有很大的局限性.为了避免反演问题的解局限于目标函数的局部最小域内，很多全局优化方法，如蒙特卡洛方法，包括属于经典蒙特卡洛方法范畴的模拟退火算法［3－4］、遗传算法［5－9］，以及一些新方法，如相邻算法［10－11］等也被应用于接收函数反演问题.刘启元等［12］根据Tarantola［13］的非线性反演理论，提出了根据接收函数径向与垂向分量复谱比的非线性反演.然而，在采用这些非线性反演方法的过程中，对于反演结果的非惟一性，一般采用两种办法进行处理.一种是基于误差相对于研究参数变化统计关系的一些假定，利用经典的线性化理论进行分析计算［2］；另一种是在网格搜索过程中引入bootstrap重新采样［14］.

对于线性化反演方法，其中以Ammon［1］的方法最具代表性，由于采用了Randall的高效算法［15］计算微分地震图，以及Shaw和Orcutt的跳跃反演技术［16］，因此反演效率极高，并且被地球物理学家广泛采用.Ammon的研究［1］表明，接收函数反演结果在很大程度上取决于初始模型的选取.如果初始模型选取合理，则只需要有限次数的迭代即可收敛到非常接近于真实结构，因此如何获取合适的初始模型是反演计算的关键.为了抑制反演的非惟一性，Julia［17］充分利用接收函数对深度变化敏感、面波频散对S波速度值变化敏感的特点，采用了接收函数与面波频散联合反演［17］.虽然联合反演在一定程度上抑制了反演的非惟一性，但反演结果还是很依赖于初始模型.另外，联合反演也受到观测条件的限制.针对这一反演问题，吴庆举等［18－19］基于小波变换多分辨率分析的特点，提出了一种用二进离散小波变换反演宽频带接收函数的方法，将宽频带接收函数在5阶分辨尺度上展开，分解到不同频段，从而将宽频带地震波形反演问题分解成不同分辨尺度的反问题，由高阶到低阶分别对不同分辨尺度的地震波形进行反演，并以n阶尺度的反演结果作为n－1阶尺度的初始模型.二进离散小波变换反演是一种广义的线性化反演方法，对反演结果的非惟一性有一定的约束，但对第5阶尺度进行反演时，还是需要提供初始模型，因此，最终的反演结果还是依赖于初始模型的选取.

在实际反演中，选取反演的初始模型主要参考已有的研究结果，为了最大限度地消除接收函数反演的不惟一性，选取充分接近真实模型的初始模型是关键.本文用不同的低通滤波参数对接收函数进行滤波，并获取相应的视入射角，基于半空间的入射波理论得到介质的S波视速度［20］，从接收函数中提取模型信息.通过数值实验总结出低通滤波参数与影响深度的关系，利用Ps震相的延时与深度的关系［2］，由浅到深剥离出各层的S波速度，并以此作为反演的初始模型.

2 线性反演与初始模型

2.1 接收函数的线性化反演

接收函数反演就是将波形中包含的信息，转化为参数化的地壳模型结构，其对应的正演问题可表达为［1］

式中，d是接收函数波形构成的矢量，F代表作用于模型m以生成接收函数d的泛函，m代表参数化后的模型空间.（1）式所表达的泛函关系是非线性的，但在初始模型m0非常靠近真实模型m的情况下，可将观测接收函数在初始模型m0附近进行Taylor展开，将问题线性化［1］

这里，δm是模型修正矢量，D是泛函F在m0处的偏导数矩阵，即Jacobi矩阵.线性化反演就是利用（2）式逐步迭代，不断修正参数化的模型矢量，最终逼近真解.因此，如何获取一个充分接近真实模型的反演初始模型是线性化反演问题的关键.

2.2 从接收函数中获取初始模型

一束平面P波从均匀半空间入射到自由表面，真入射角iP、视入射角iP、水平慢度（射线参数）p、半空间的S波速度VS以及P波速度VP之间有如下关系［20］：

变换（3）式可以得到

这里，视入射角iP可表达为［20］

其中，RRF代表径向接收函数，ZRF代表垂直向接收函数.利用接收函数计算视入射角要比直接利用原始记录来得方便，免去了直接用原始记录读取震相的麻烦.给接收函数加上低通滤波平滑因子后，可将视入射角和半空间S波速度表达为低通滤波参数T的函数，L.Svenningsen和B.H.Jacobsen［20］将这样得到的半空间S波速度称为S波视速度VS，app.

为了检验上述方法，我们以一层地壳覆盖在半空间之上的模型为例，图1a中给出的是S波速度随深度的变化规律，地壳的S波速度为3.50km／s，上地幔的S波速度为4.50km／s，若泊松比σ取0.25，可利用经验关系：

给出密度ρ，以此确定地壳模型.我们利用Kennett提出的传播矩阵法［21］来计算地震响应地震图，分别对径向分量和垂直分量进行反褶积得到相应的接收函数，利用方程（6）对相应的接收函数进行平滑，得到如图1b所示的视速度随滤波参数的变化曲线.从图1中可看出，滤波参数很小时，视速度值与模型值非常接近，随着滤波参数的增大视速度也呈增加的趋势.视速度VS，app关于滤波参数T的一阶导数在一定程度上体现了S波速度随深度的变化率，在导数最大的地方就是S波速度相对于深度变化最剧烈的地方，这意味着该影响深度可能就是界面的深度.通过计算，我们发现在4s附近视速度随滤波参数的变化率最大，而理论模型的地壳厚度是20km，若以滤波参数乘以倍数因子5作为其对应的影响深度，则视速度的最大变化率发生在20km附近（如图1），这与理论模型具有一定的相关性.由（6）式得到的VS，app，在滤波参数小于Ps震相走时的情况下，只有直达P波对径向接收函数RRF（t＝0）有贡献，此时得到的VS，app就是地表附近的绝对S波速度；而随着滤波参数的增大，影响深度越来越大，得到的VS，app是等效半空间所包含的各层的平均效果［20］.因此，在第一个分层点得到的S波速度可认为是第一层的绝对S波速度，而在第二个分层点得到的是将一、二两层等效为一层时的结果，对于多层的情况，依次类推.考虑到Ps震相的延时与层厚和S波速度有如下关系［2］：

一般情况下，波速比κ可取值1.732，我们可以先计算出第一层的，以及一、二两层等效为一层的，由（8）式可知即为第二层的.在已知厚度和波速比的情况下，由（8）式即可反推第二层的S波速度.依次类推，即可由浅入深剥离出各层的绝对S波速度.

另外，随着滤波参数T的增加，影响深度不断增大，越来越多的震相对径向接收函数RRF（t＝0）产生影响，浅层结构的贡献越来越小，因此可取滤波参数较大时VS，app随滤波参数变化的渐近趋势作为Moho面以下的S波速度，由此得到速度随深度变化的模型如图1c所示.对比图1a与1c，从接收函数中所提取的地壳S波速为3.55km／s，上地幔S波速度为4.40km／s，这一结果与理论模型非常接近，然而，厚度却有一定的差异.

3 数值实验

3.1 简单模型

一般而言，在地球内部速度随深度增加而增加.如图2所示，若地壳由厚度分别为10km、10km、20km，S波速度分别为3.00km／s、3.50km／s、3.80km／s的三层组成，波速比取为1.732，按上述的经验公式确定各层的密度.利用该模型合成的理论地震图经反褶积后得到相应径向接收函数如图2所示.反演的任务就是通过拟合图2中的接收函数，以提取相应的地壳S波速度结构.由于地壳结构比较简单，各界面上产生的Ps震相很容易分辨，Moho面的Ps震相的延时为5s，经Ps相与直达P的延时估算地壳厚度为40km.若没有其他约束信息，可考虑到地壳S波平均速度在3.5km／s左右，我们给出一个由20层厚度为2km、S波速度为3.5km／s的模型作为反演的初始模型，利用Ammon［1］的线性化反演程序进行反演计算，整个迭代过程快速地向真解逼近，第5次反演结果在Moho面以上已基本与真解重合，接收函数波形也达到99%的拟合度（如图3）.然而，若将地壳的平均速度取为3.6km／s，再次进行反演时，反演结果却与真解出现了较大的偏差.如图4所示，虽然接收函数波形达到了99%的拟合度，但第2、3层的速度值有明显差异，并且Moho面的深度也不准确.两次反演使用的初始模型Moho面深度都与真实模型一致，惟一的区别就在于S波速度值，取3.5km／s则刚好与真实模型的第二层一致，而取3.6km／s则与真实模型每一层的速度值都有差异.这个试验充分说明接收函数反演严重依赖于初始模型的速度值.

图1 （a）半空间上覆盖一层的理论模型；（b）S波视速度与滤波参数的关系曲线；（c）从S波视速度与滤波参数关系曲线获取的S波速度结构Fig.1 （a）The theoretical model of the single layer over a half－space；（b）The relation curve between the apparent velocity of S wave versus to filtering parameter；（c）S－velocity structure acquired from the curve illustrated in（b）

图2 （a）由（b）所示地壳模型合成的径向接收函数（高斯参数α＝2.0）；（b）半空间上覆盖三个水平层的地壳模型Fig.2 （a）Synthetic radial receiver function calculated from the model（b）（Gaussian parameterα＝2.0）；（b）The crustal model of three－layer over a half－space

图3 （a）最终反演模型（第5次迭代）的合成波形与观测波形的拟合情况（高斯参数α＝2.0）；（b）反演所得到的S波速度结构.黑色粗线表示图2b所示的真实模型、黑色虚线表示由经验方法获取的初始模型（泊松比σ＝0.25，地壳平均S波速度为3.5km／s）、黑色细线表示1～4次反演迭代的结果，灰色粗线表示最终反演结果Fig.3 （a）The observed waveform corresponding to the model illustrated in Fig.2band the synthetic waveform calculated from the inversion result（Gaussian parameterα＝2.0）；（b）The S－wave velocity structure from the inversion iteration.Black thick line represents true model illustrated in Fig.2b，black dash line represents the initial model（Poisson′s ratioσ＝0.25，the average crustal velocity of S wave is 3.5km／s）obtained from the empirical method，black thin lines represent results of the 1～4th inversion iterations，gray thick line represents the final result

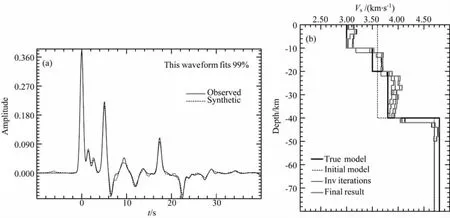
图4 同图3，但初始模型地壳S波速度变为3.6km／sFig.4 Same as Fig.3，but average S－wave velocity of the crust is perturbed to 3.6km／s

图5 （a）真实模型（如图2b所示）；（b）S波视速度与滤波参数的关系曲线；（c）从S波视速度与滤波参数关系曲线（b）中获取的S波速度结构Fig.5 （a）The true model illustrated in Fig.2b；（b）The relation curve between the apparent velocity of S wave versus to filtering parameter；（c）S－velocity structure acquired from the curve illustrated in（b）

图6 同图3，但采用如图5c所示初始模型Fig.6 Same as Fig.3，but the initial model is replaced by the one illustrated in Fig.5c

对于同一个例子，作为对比分析，我们利用等效半空间理论得到S波视速度VS，app和滤波参数T的关系如图5b所示.从图5中可看出，滤波参数T＜2s时的视速度值与真实模型的第一层速度值很接近，滤波参数T＞19s时的视速度值与真实模型的半空间的速度值很接近.利用分层点选取原则建立的初始模型与真实模型值已很接近，仍有三层结构，但是，初始模型不仅层厚与真实模型有一定的差异，而且Moho面的深度仅为32km，这与真实模型存在较大的偏差.以图5c所示的S波速度结构为基础，将每一层分为厚度为2km的薄层，利用前述方法确定P波速度和密度以建立反演的初始模型.如图6所示，经过五次反演迭代计算，反演过程快速地向真解逼近，最终反演结果（第5次迭代）Moho面以上各层的S波速度值已基本与真实模型重合，仅在Moho面以下稍有差异.

3.2 复杂模型

上面的例子正如Ammon［1］所论述的那样，接收函数反演结果严重依赖于初始模型的选取.为了对比分析，现在选取Ammon［1］所采用的包含低速层的复杂地壳模型进行数值实验.如图7所示，S波速度随着深度增加而增加，但深度在30km附近存在一厚度为4km的低速层，从模型中计算出的理论接收函数也表明，Ps相较为复杂，存在多个Ps相，其中，来自Moho面的Ps出现在5.5s处.下面就尝试用不同的初始模型来拟合该理论接收函数.

由于本例中的地壳厚度为44km，与上一节中的很接近，我们同样给出一个由22层厚度为2km、S波速度为3.5km／s的地壳模型作为反演的初始模型，进行迭代.虽然初始模型的Moho面深度与真实模型一致，如图8所示，经过五次反演迭代后，波形拟合度达到了98%，反演结果中也捕捉到了低速层，但低速层以及Moho面的深度是不准确的.说明反演过程中，接收函数对深度变化敏感的特点都没有得到发挥，另外，各层的S波速度值和真实模型相差较大.对于这样一个复杂的模型，若没有可靠的速度值作为约束条件，即使Moho面深度精确给出，也不能有效抑制反演的不惟一性.

图7 （a）由（b）所示地壳模型合成的径向接收函数（高斯参数α＝2.0）；（b）Ammon［1］采用的含低速层的地壳模型Fig.7 （a）Synthetic radial receiver function calculated from the model（b）（Gaussian parameterα＝2.0）；（b）The crustal model with a low velocity used by Ammon［1］

图8 同图3，但采用如图7所示地壳结构和接收函数作为真实模型和观测波形Fig.8 Same as Fig.3，but the true model and observed waveform are replaced by the ones illustrated in Fig.7

对于同一个模型，我们从低通滤波后的接收函数中获取S波视速度VS，app和滤波参数T的关系曲线如图9所示，并利用前述分层点选取原则得到相应的初始模型.初始模型（图9c）由4层组成，层厚与真实模型有较大差异，而且不含低速层.不过，在浅部，初始模型的速度值与真实模型很接近.为了更好地拟合接收函数，我们将初始模型的每一层均拆分为厚度为2km的薄层，经过五次反演迭代，反演过程快速地逼近“真实”模型（图10），并准确地捕捉到了低速层.

为了检验反演过程对模型参数的敏感性，我们在理论接收函数滤波频段上增加了10%的随机噪声，并且对初始模型的波速比分别进行5%的正负扰动，即泊松比分别取为0.23和0.27，再次进行反演计算.反演迭代过程如图11和图12所示，经过5次迭代，虽然波形拟合度不高，但反演结果仍然快速地向真实模型逼近.另外，低速层和Moho面的捕捉仍然非常准确，壳内各层的S波速度值也与真实解吻合得非常好.

3.3 实际观测数据实验

图9 （a）“真实”模型（如图7b所示）；（b）S波视速度与滤波参数的关系曲线；（c）从S波视速度与滤波参数关系曲线（b）中获取的S波速度结构Fig.9 （a）The“ture”model illustrated in Fig.7b；（b）The relation curve between the apparent velocity of S wave versus to filtering parameter；（c）S－velocity structure acquired from the curve illustrated in（b）

图10 （a）最终反演模型（第5次迭代）的合成波形与观测波形的拟合情况（高斯参数α＝2.0）；（b）反演所得到的S波速度结构.黑色粗线表示图7b所示的真实模型、黑色虚线表示用本文方法获取的初始模型（即图9c，泊松比σ＝0.25）、黑色细线表示1～4次反演迭代的结果，灰色粗线表示最终反演结果Fig.10 （a）The observed waveform corresponding to the model illustrated in Fig.2band the synthetic waveform calculated from the inversion result（Gaussian parameterα＝2.0）；（b）The S－wave velocity structure from the inversion iteration.Black thick line represents true model illustrated in Fig.2b，black dash line represents the initial model obtained from the study（showed in Fig.9c，Poisson′s ratioσ＝0.25），black thin lines represent results of the 1～4th inversion iterations，gray thick line represents the final result

云南地区有长达几百公里的测深剖面，为检验反演结果提供了条件.虽然数值实验取得了较好的反演结果，为了检验实际观测数据的反演效果，我们从云南保山台记录的远震事件提取了接收函数波形（如图13所示），事件震中距为6520km.由于震相比较清晰，可以看到Ps震相延时约为5s左右，由此可估计Moho面深度约为40km.我们先采用本文的方法，用不同的低通滤波参数对接收函数进行滤波，得到S波视速度与滤波参数的关系曲线，再利用剥层技术获取用于反演的初始模型.最后，反演得到了保山台下方的S波速度结构（如图13c）.为了与前人的结果作对比，我们收集了胡家富等［22］的接收函数反演结果（图13c细实线），以及人工测深的结果［23］.由于人工测深给出的是P波速度，这里利用保山台的泊松比［22］换算为S波速度（图13c粗虚线和细虚线）.与已有的接收函数反演结果相比，虽然Moho面的深度较为一致，但本文所得结果更接近人工测深结果，尤其是在上地幔里更接近测深结果.另外，胡家富等的反演结果在22km附近有一个明显的低速层，而本文的反演结果在这个位置没有明显的低速结构，这与爆破地震研究结果较为一致.

图11 同图10，但在观测波形的滤波频段上加入了10%的随机噪声，初始模型泊松比取0.23Fig.11 Same as Fig.10，but the observed waveform is mixed with 10%random noise，and the Poisson＇s ratio of the initial model is perturbed to 0.23

图12 同图10，但在观测波形的滤波频段上加入了10%的随机噪，初始模型泊松比取0.27Fig.12 Same as Fig.10，but the observed waveform is mixed with 10%random noise，and the Poisson＇s ratio of the initial model is perturbed to 0.27

4 讨论与结论

Ammon［1］的线性化反演算法在体现高效的同时，由于引入了平滑约束，在初始模型的选取上给予了一定程度的灵活性.不同的初始模型只要提供了足够相容的约束信息，都会向同一个解收敛.因此当初始模型发生扰动时，不会使最终结果过于发散，从而保障了反演结果的稳定性和可靠性.数值实验表明，当地壳结构简单时，通过Ps震相的延时判断出Moho面深度，并取地壳平均S波速度为3.5km／s作为初始模型，也可能使反演过程向真解收敛，但前提是地壳平均S波速度值能为反演提供足够准确的约束.但在地壳结构比较复杂的情况下，选取一个简单的初始模型将导致反演严重偏离真实解.其原因主要是各层真实速度值偏离地壳平均速度值较大所致，此时仅依靠Moho面深度和地壳平均S波速度的约束肯定是不够的，还必须提供更多的分层信息.

图13 （a）保山台记录的远震事件三分量波形（震中距6520km）；（b）观测径向接收函数（实线）和反演模型的合成波形（虚线）的拟合情况（高斯参数α＝2.0）；（c）细实线表示参考模型［22］，粗虚线为爆破地震保山（南）炮点的速度结构［23］，细虚线为爆破地震保山（北）炮点的速度结构［23］，粗实线为本文的反演结果Fig.13 （a）Teleseismic 3－component waveforms recorded by Station BS（dist＝6520km）；（b）Radial receiver function（solid line）calculated from（a）and synthetic radial receiver function（dash line）calculated from the final inversion result（α＝2.0）；（c）Thin solid line represents the reference model［22］，thick dash line represents S－velocity structure of the south explosion point of Baoshan［23］，thin dash line represents S－velocity structure of the north explosion point of Baoshan［23］，thick solid line represents the inversion result calculated from the initial model acquired with our method.

由于接收函数具有对深度变化敏感、而对速度值变化不敏感的特点，如果初始模型能在几个地层的S波速度值上提供准确的约束，即使深度不准确，反演结果仍然可以向真解收敛.对于包含低速层的复杂地壳模型，仅仅依靠Moho面深度和地壳平均S波速度值的约束是不够的，Moho面以上需要区分出更多的层次才能提供足够的约束.本文根据不同滤波参数下，从低通滤波后的接收函数获取的视入射角不同，影响深度也不同，利用经验关系从视速度随滤波参数的变化曲线中提取了S波速度结构，与真实模型相比，速度值整体变化趋势非常接近，但每一层的深度可能存在较大差异.这样选取有利于充分发挥接收函数对深度变化敏感的优势，由于速度值提供了有效的约束，虽然Moho面深度并不准确，但反演迭代过程还是快速地向真解逼近.另外，通过给真实波形加入10%的噪声，在保待S波速度值不变的情况下，分别对波速比进行5%的正负扰动（即泊松比分别扰动为0.23和0.27），反演结果仍然是快速向真解收敛.最后我们用本文方法对保山台实测远震事件数据进行实验，并与前人的接收函数反演结果和测深结果进行对比，可以发现用本文方法反演得到的结果与测深结果更加吻合.这充分说明只要S波速度值能够提供准确的约束，接收函数的反演过程对P波速度的选取并不敏感.

接收函数反演具有很强的非惟一性，正演合成波形的拟合度并不足以说明解的好坏，反演结果是否接近于真实情况在很大程度上取决于初始模型的选取，这是由于线性化过程的特点所决定的.当前很多学者一般都倾向于采用其他研究者的结果作为反演计算的初始模型，但这样引用的初始模型是否就一定会向真解收敛是很难论证的，甚至会陷入一个死循环，从而导致结果更加偏离真实解.刘启元等［24］发展了基于贝叶斯反演理论的接收函数与环境噪声的非线性联合反演方法，在反演过程中利用环境噪声的相速度频散数据对地壳S波绝对速度提供了有力的约束，使得反演结果对初始模型的依赖程度大大降低.然而，该方法在实施过程中需要密集的地震台网覆盖，对观测条件的要求较高.本文尝试从接收函数所包含的信息中提取初始模型，使初始模型就局限在最靠近真解的解空间内，通过S波速度值提供有效的约束，有效地抑制了反演的非惟一性.

（References）

［1］ Ammon C J，Randall G E，Zandt G.On the nonuniqueness of receiver function inversions.J.Geophys.Res.，1990，95（B10）：15303－15318.

［2］ Zhu L P，Kanamori H.Moho depth variation in southern California from teleseismic receiver functions.J.Geophys.Res.，2000，105（B2）：2969－2980.

［3］ Sen M K，Stoffa P L.Nonlinear one－dimensional seismic waveform inversion using simulated annealing.Geophysics，1991，56：1624－1638.

［4］ 刘鹏程，纪晨，Hartzell S H.改进的模拟退火－单纯形综合反演方法.地球物理学报，1995，38（2）：199－205.Liu P C，Ji C，Hartzell S H.An improved simulated annealing－downhill simplex hybrid global inverse algorithm.Chinse J.Geophys.（in Chinese），1995，38（2）：199－205.

［5］ Sambridge M，Drijkoningen G.Genetic algorithms in seismic waveform inversion.Geophys.J.Int.，1992，109（2）：323－342.

［6］ Sen M K，Stoffa P L.Rapid sampling of model space using genetic algorithms：examples from seismic waveform inversion.Geophys.J.Int.，1992，108（1）：281－292.

［7］ 石耀霖，金文.面波频散反演地球内部构造的遗传算法.地球物理学报，1995，38（2）：189－198.Shi Y L，Jin W.Genetic algorithms inversion of lithospheric structure from surface wave dispersion.Chinese J.Geophys.（in Chinse），1995，38（2）：189－198.

［8］ 吴建平，明跃红，汤毅.遗传算法在上地幔速度结构研究中的应用.地震地磁观测与研究，1997，18（2）：11－29.Wu J P，Ming Y H，Tang Y.Application of genetic algorithm in study of upper mantle velocity structure.Seismological and Geomagnetic Observation and Research（in Chinese），1997，18（2）：11－29.

［9］ 吴建平，明跃红，曾融生.遗传算法中的光滑约束反演及其在青藏高原面波研究中的应用.地震学报，2001，23（1）：45－53.Wu J P，Ming Y H，Zeng R S.Smooth constraint inversion technique in genetic algorithms and its application to surface wave study in the Tibetan plateau.Acta Seismologica Sinica（in Chinese），2001，23（1）：45－53.

［10］ Sambridge M.Geophysical inversion with a neighbourhood algorithm—Ⅰ.Searching aparameter space.Geophys.J.Int.，1999，138（2）：479－494.

［11］ Sambridge M.Geophysical inversion with a neighbourhood algorithm－II.Appraising the ensemble.Geophys.J.Int.，1999，138：727－746.

［12］ 刘启元，Kind R，李顺成.接收函数复谱比的最大或然性估计及非线性反演.地球物理学报，1996，39（4）：502－513.Liu Q Y，Kind R，Li S C.Maximal likelihood estimation and nonlinear inversion of the complex receiver function spectrum ratio.Chinese J.Geophys.（in Chinese），1996，39（4）：502－513.

［13］ Tarantola A.Inverse Problem Theory，Method for Data Fitting and Model Parameter Estimation.Amsterdam：Elsevier，1987.

［14］ Sandvol E，Seber D，Calvert A，et al.Grid search modeling of receiver functions：implications for crustal structure in the Middle East and North Africa.J.Geophys.Res.，1998，103（B11）：26899－26917.

［15］ Randall G E.Efficient calculation of differential seismograms for lithospheric receiver functions.Geophys.J.Int.，1989，99（3）：469－481.

［16］ Shaw P R，Orcutt J A.Waveform inversion of seismic refraction data and applications to young Pacific crust.Geophys.J.R.Astron.Soc.，1985，82（3）：375－414.

［17］ JuliàJ，Ammon C J，Herrmann R B，et al.Joint inversion of receiver function and surface wave dispersion observations.Geophys.J.Int.，2000，143（1）：99－112.

［18］ Wu Q J，Li Y H，Zhang R Q，et al.Wavelet modeling of broad－band receiver functions.Geophys.J.Int.，2007，170（2）：534－544.

［19］ 吴庆举，田小波，张乃铃等.用小波变换方法反演接收函数.地震学报，2003，25（6）：601－607.Wu Q J，Tian X B，Zhang N L，et al.Inversion of receiver function by wavelet transformation.Acta Seismologica Sinica（in Chinese），2003，25（6）：601－607.

［20］ Svenningsen L，Jacobsen B H.Absolute S－velocity estimation from receiver functions.Geophys.J.Int.，2007，170（3）：1089－1094.

［21］ Kennett B L N.Seismic Wave Propagation in Stratified Media.Cambridge：Cambridge University Press，1983.

［22］ 胡家富，苏有锦，朱雄关等.云南的地壳S波速度与泊松比结构及其意义.中国科学（D辑），2003，33（8）：714－722.Hu J F，Su Y J，Zhu X G，et al.S－wave velocity and Poisson′s ratio structure of crust in Yunnan and its implication.Science in China（Series D）（in Chinese），2002，33（8）：714－722.

［23］ 胡鸿翔，陆涵行，王椿镛等.滇西地区地壳结构的爆破地震研究.地球物理学报，1986，29（2）：133－144.Hu H X，Lu H X，Wang C Y，et al.Explosion investigation of the crustal structure in western Yunnan Province.Chinese J.Geophys.（in Chinese），1986，29（2）：133－144.

［24］ 刘启元，李昱，陈九辉等.基于贝叶斯理论的接收函数与环境噪声联合反演.地球物理学报，2010，53（11）：2603－2612.Liu Q Y，Li Y，Chen J H，et al.Joint inversion of receiver function and ambient noise based on Bayesian theory.Chinese J.Geophys.（in Chinese），2010，53（11）：2603－2612.

An effective technique to constrain the non－uniqueness of receiver function inversion

PENG Heng－Chu，HU Jia－Fu＊，YANG Hai－Yan，WEN Li－Min
Department of Geophysics，Yunnan University，Kunming650091，China

The relation curve between the apparent velocity of S wave and the filter－parameter is obtained by low－pass filtering the radial and vertical receiver function，then it is transformed into the S velocity structure beneath the station with empirical formula；moreover，the S velocity structure will be regarded as initial model for receiver function inversion.The numerical simulation indicated that the inversion processes would approach quickly to the true model once the initial S velocity can supply the effective constraint to inversion，even if the depth of Moho is not accurate.In addition，for the same initial S structure，the inversion results also approach to the true model quickly，even adding 10%of random noises to the“observed”receiver function，and 5%of positive and negative perturbation to the velocity ratio（corresponding to the Poisson′s ratio of 0.27and 0.23）respectively.We processed the teleseismic receiver function recorded by Baoshan station.The result from our method is similar to that of sounding section.These confirmed that the inversion processes of receiver function are not sensitive to the initial P velocity if the initial S wave velocity can provide the effective constraint information.

Receiver function，Inversion，Initial model

10.6038／j.issn.0001－5733.2012.04.013

P315

2011－08－08，2012－03－09收修定稿

国家自然科学基金（U0933602）和云南省基金资助项目（2007D013M）资助.

彭恒初，男，讲师，2004年毕业于北京大学，获硕士学位，研究方向为深部地球物理.E－mail：terrypku＠163.com

＊通讯作者胡家富，E－mail：jfhu＠ynu.edu.cn

彭恒初，胡家富，杨海燕等.接收函数反演地壳S波速度结构的有效约束方法.地球物理学报，2012，55（4）：1168－1178，

10.6038／j.issn.0001－5733.2012.04.013.

Peng H C，Hu J F，Yang H Y，et al.An effective technique to constrain the non－uniqueness of receiver function inversion.Chinese J.Geophys.（in Chinese），2012，55（4）：1168－1178，doi：10.6038／j.issn.0001－5733.2012.04.013.

（本文编辑 胡素芳）