均匀弹性分层介质模型中的同震位移、应变以及应力

郝金来，姚振兴

中国科学院地质与地球物理研究所，北京 100029

均匀弹性分层介质模型中的同震位移、应变以及应力

郝金来，姚振兴

中国科学院地质与地球物理研究所，北京 100029

地震发生时产生的同震位移、应变以及应力变化，特别是同震应力的变化，在地震触发等问题的研究中有着重要的意义.本文进一步发展了基于均匀弹性水平层状介质，利用广义反射透射系数矩阵和离散波数计算同震位移的方法，使之可以计算相应的应变、应力以及同震库仑应力变化.可适用于多种情况，接收点可以位于地表以及地表以下，震源类型可以是剪切位错源以及拉张位错源.通过与半无限介质的解析解相比较，结果一致，验证了方法的可靠性以及计算精度，可以用于计算地震之后库仑应力变化，为判断余震分布提供参考.在计算同震位移时，使用了梯形积分与Filon积分相结合的积分方式，即提高了同震位移计算的速度，又保证了计算精度，有利于反演问题研究.

广义反射透射系数矩阵，离散波数，同震位移，库仑应力，均匀分层弹性介质

1 引 言

在地震学研究中地震发生时产生的同震位移、应变以及应力变化有着非常重要的研究意义，同震位移可用于反演断层破裂过程，应力变化可用于地震成因以及地震触发等研究［1－3］.地震发生后，周边某些断层上库仑应力增大，加大了断层破裂的几率，相反则减少了断层上的负载［4－7］.在许多研究区域都找到了库仑应力与余震分布、地震触发的对应关系，例如1999年土耳其伊兹米特地震与杜赛地震等［8］.因此，计算地震发生后的同震位移、应变、应力变化是一项重要的基础工作.

自从Steketee［9］首次将静力学位错理论引入地震学后，有关计算静态位移场的理论研究迅速发展起来.根据介质模型的不同，主要有以下几类，首先是基于弹性半无限介质模型的计算方法［10－11］，Okada［12－13］详细地评述了有关的研究工作，给出了半无限介质内位错点源和有限源静态位移场的解析解.这种方法的优点是给出的结果为解析解，计算速度快，缺点是模型过于简单，特别是当地表存在低速层时，半无限介质模型给出的结果往往会存在较大误差［14］.因此发展起来了基于均匀弹性层状介质的相关理论，Sato和Matsu′ura［14］，Ben－Menaham和Singh［15］，Singh［16］，Wang等［17］给出了水平层介质中的计算方法.Israel等［18］，Pollitz［19］给出了球体分层模型中的计算方法.层状模型可以较好地模拟地球介质.但模拟震后较长时间间隔内的位移、应变、应力变化时，黏弹性松弛效应的影响则不可忽略［20－22］，弹性模型无法考虑这一点，而黏弹性层状介质模型可以更好地拟合这种震后形变.随着计算能力的增强，利用有限元等方法，基于更复杂的横向不均匀介质模型计算应力变化，在近些年逐渐得到更广泛地应用［23－24］.这些不同的模型有其自身的适用范围，可以根据不同的研究目的选择合适方法加以利用.本文主要考虑均匀弹性水平层状介质模型下，静力学位移、应变、应力的计算.

在计算理论地震图时，Kennett［25－26］发展了反射和透射系数矩阵方法，Bouchon［27］发展了一种可以有效地计算波数积分的离散波数方法，Yao和Harkrider［28］将两者相结合，利用广义反射透射系数矩阵和离散波数方法计算近场理论地震图.谢小碧和姚振兴［29］把这种处理波动问题方法加以推广，用以处理静态问题，给出了均匀弹性分层介质中剪切位错点源在地面产生的静态位移场的解答，He等［30］给出了拉张源所产生的静态位移场的解答.但是他们均未给出相应的应变、应力的计算方法与结果.在他们工作的基础上，我们进一步发展该方法，使之可以基于均匀分层弹性介质模型，根据广义反射透射系数矩阵和离散波数方法，计算同震应变、应力变化等.

谢小碧和姚振兴［29］，He等［30］计算同震位移时，均采用了简单的梯形积分方式.积分间隔的选取将直接影响到计算精度与速度，较小的积分间隔才能得到较为精确的数值解，但是这样会增加计算时间，对于利用同震位移资料进行反演问题研究十分不利.理论地震图计算中广泛采用的Filon积分方法［31－33］，可以使得在选取较大的积分间隔时，计算精度仍然很高.在本文中，计算同震位移时，使用梯形积分与Filon积分相结合的方法，即提高了计算速度，又使得计算结果具有较高精度.

在本文主要考虑的均匀弹性水平层状介质模型中，前人研究主要存在以下一些问题：某些研究中震源类型并不全面，特别是拉张源的计算；某些研究中仅给出了位移的计算结果；某些研究中水平层的数量受到制约等［17］.Wang等［17］给出了一种全面的计算方法，使用了Thomson－Haskell矩阵进行计算，矩阵元素中存在导致溢出问题的指数项.Wang等［17］通过一些方法，如正交归一化等避免这些问题的出现.而广义反射透射系数矩阵摒弃了造成数值不稳定的指数项，解决了数值溢出等问题，因此我们利用广义反射透射系数矩阵方法计算同震位移、应变、应力变化.

2 方 法

2.1 同震应变、应力以及库仑应力的计算

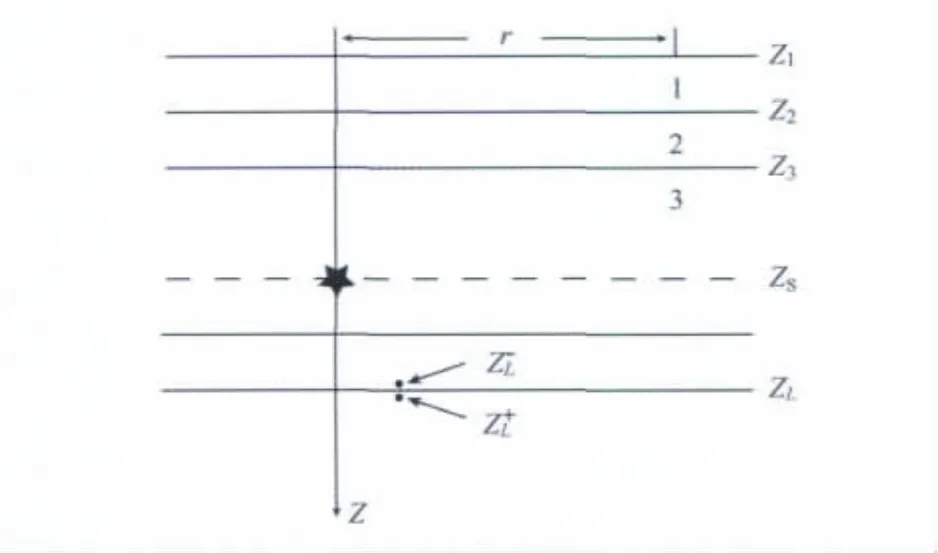
图1 水平层状介质模型水平层状介质模型，1，2，3等表示水平层状介质，Z1，Z2，Z3等表示界面，r表示震中距，五角星标示了震源的位置，即Zs层.Fig.1 Layered medium modelLayered medium model，1，2，3represent the layered medium，Z1，Z2，Z3represent the interface，r represents the epicenter distance，and the star shows the location of the source，in the interface of Zs.

根据先前的研究结果［29－30］，在如图1所示的水平层状介质中，三分量的静力学位移解答可以表示成如下形式：其中wz，qr，vθ分别表示垂向、径向和切向的静力学位移，Σ为断层面元的面积，Δui，i＝1，2，3分别对应走滑、倾滑和拉张断层的静力学位错的错距，Aim为方向因子，qm，wm，vm分别为面谐矢量坐标系下的位移分量，Jm（kr），J′m（kr）分别为m阶贝塞尔函数及其导数.

根据位移解答求应变与应力的关键步骤为求位移分量的偏导数，即求解.公式（1）中与θ有关的量仅为方向因子Aim，与r有关的量仅为贝塞尔函数及其导数与z有关的量仅为qm，wm，vm.

对θ的偏导数表示为

根据方向性因子的表达式可得到相应的偏导数：

对r的偏导数表示为

对z的偏导数表示为

当接收点位于地面或介质内部时，qmwm和vm表达式各不相同.当接收点位于地表时有

震源系数分别为

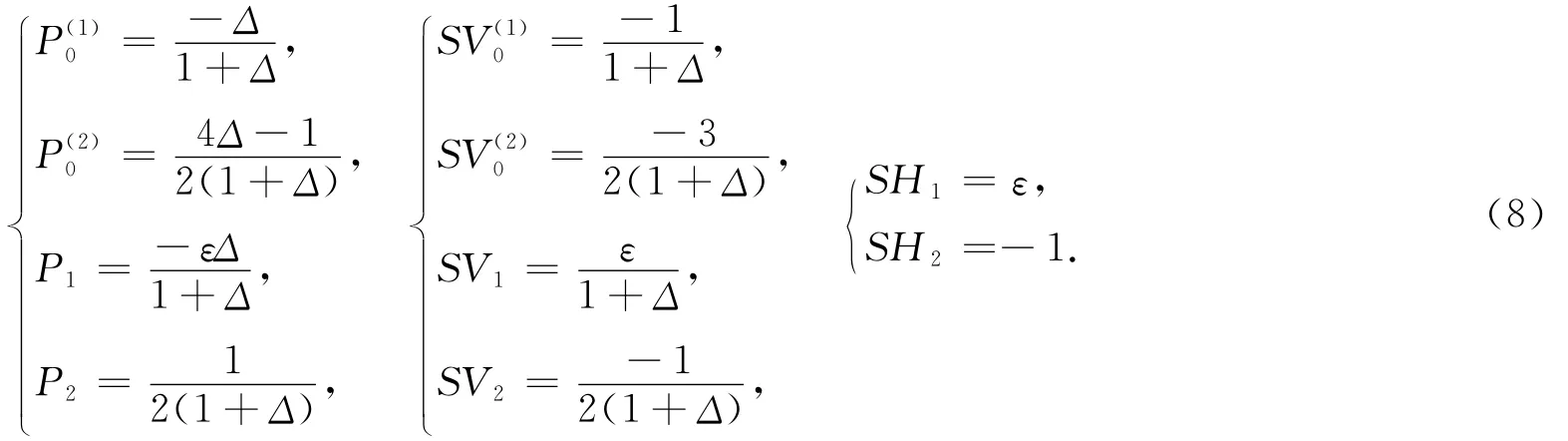
此处Pm，SVm和SHm分别表示P＋m，P－m，SV＋m，SV－m和SH＋m，SH－m，而

当接收点位于介质内部时，分接收点的深度zR小于震源深度和大于震源深度两种情况.当接收点位于震源以上时，即当zR＜zs时，有

其中接收函数矩阵和接收函数分别为

当接收点位于震源以下时，即当zR＞zs，有

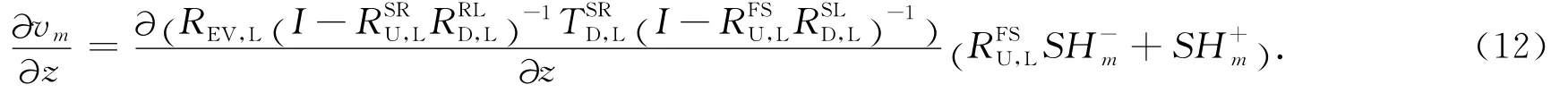
其中接收函数矩阵和接收函数分别为

根据位移的偏导数，可得到应变、应力解答分别为［34－35］

其中err，eθθ，ezz，erθ，erz，eθz为应变分量，τrr，τθθ，τzz，τrθ，τrz，τθz为应力分量，urr，uθθ，uzz，urθ，urz，uθz为位移的偏导数，λ，μ为弹性常数.根据应力张量可以计算断层面上的库仑应力变化［4，36－37］，如下式所示：

其中Δσ，Δτs，Δσn，μ′分别表示库仑应力，断层面上的剪应力，断层面上的正应力，以及等效摩擦系数.

2.2 同震位移计算中积分方式的改进

同震位移计算中的关键为计算以下积分：

为了提高计算速度，需要选取较大的积分间隔，如果此时仍使用梯形积分，将会带来较大的计算误差.当kr较大时，Jm（kr）存在渐进展开式，可以采用Filon积分方式，选取较大的积分间隔，仍会有较高的计算精度［31－33］.因此在积分的计算过程中，采用分段积分的方式.当kr较小时，选取较小的积分间隔，采用梯形积分.当kr较大时，选取较大的积分间隔，采用纪晨和姚振兴改进的Filon积分方法［32］，仅取贝塞尔函数Jm（kr）渐进展开式的零次项

这样既保证了计算精度，又提高了计算速度.

3 数值检验

为了检验公式的正确性及数值方法的精度，我们做了一系列的数值检验.分别验证均匀弹性半无限介质模型中接收点位于不同深度时，以及分层介质模型中接收点位于地表时，点源产生的位移以及应力解的正确性.在笛卡尔坐标系中，设定沿着断层走向为X轴正方向，逆时针旋转90°为Y轴正方向，垂直向上为Z轴正方向，断层左上角对应于地表的投影点为坐标原点，如图2所示.

图2 坐标系示意图Fig.2 The coordinate system

3.1 接收点位于地表时的点源检验

均匀弹性半无限介质参数设定为P波速度4.0km／s，S波速度2.7km／s，密度2.5g／cm3.使用10层，每层厚度为3km，具有相同P波速度，S波速度以及密度的均匀弹性介质层，之下设置为半无限，用来模拟均匀弹性半空间.震源参数设定如下：倾角为70°，断层面积0.01km×0.01km，震源深度5.0km.接收点参数设定如下：接收点位于地表，在笛卡尔坐标系中，接收点横坐标3.0km，纵坐标从－10.0km起始，到10.0km截止，共取41个点.分别计算了走滑断层、倾滑断层以及拉张断层所产生的位移以及应力结果，并将之与Okada给出的解析解［12－13］进行了对比.图3a，图3b分别给出了位移，应力结果的对比图，由于接收点位于地表，相应的应力分量只有径向、切向正应力以及径向与切向之间的剪应力.与解析解相比较，两者一致.

3.2 接收点位于地下，深度小于震源深度时的点源检验

采用与3.1相同的介质设定，震源参数设定如下：倾角为70°，断层面积0.01km×0.01km，震源深度20.0km，接收点设定如下：接收点位于地下，深度16.0km，接收点横坐标3.0km，纵坐标从－10.0km起始，到10.0km截止，共取41个点.图4a，图4b分别给出了位移，应力结果与Okada的解析解［12－13］的对比图，两者一致.

3.3 接收点位于地下，深度大于震源深度时的点源检验

采用与3.1节相同的介质设定，震源参数设定如下：倾角为70°，断层面积0.01km×0.01km，震源深度10.0km，接收点设定如下：接收点位于地下，深度14.0km，接收点横坐标3.0km，纵坐标从－10.0 km起始，到10.0km截止，共取41个点.图5a，图5b分别给出了位移，应力结果与Okada的解析解［12－13］的对比图，两者一致.通过以上数值检验可以看出，基于均匀弹性分层介质模型，根据广义反射透射矩阵和离散波数方法计算出的位移与应力结果与解析解一致，验证了公式的正确性以及计算的精度.

3.4 分层介质中接收点位于地表的点源检验

选取如表1所示的均匀弹性水平层状介质模型，将接收点设置于地表，计算点源产生的位移以及应力解，通过与Wang等（2003）的计算结果比较，验证在分层介质中的数值计算精度.震源参数设定如下：倾角为70°，断层面积0.01km×0.01km，震源深度5.0km.接收点参数设定如下：接收点位于地表，在笛卡尔坐标系中，接收点横坐标3.0km，纵坐标从－10.0km起始，到10.0km截止，共取41个点.计算了走滑断层与倾滑断层所产生的位移以及应力结果，图6给出了位移，应力结果的对比图，由于接收点位于地表，相应的应力分量只有径向、切向正应力以及径向与切向之间的剪应力.由图可见，两者一致.

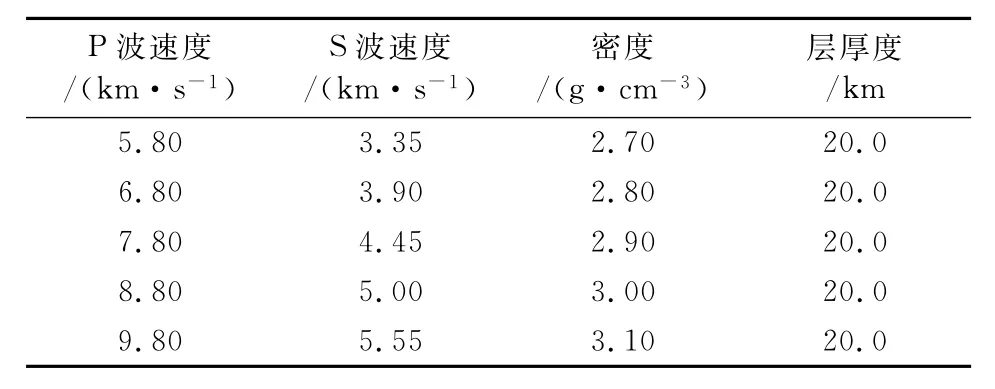
表1 分层介质模型Table 1 Layered velocity model

4 库仑应力的计算

根据计算出的同震应力张量，即可得出断层面上的静态库仑应力变化，用于地震触发研究［4］.考虑一个断层，走向0°，倾角70°，滑动量1m，滑动角45°，断层长度20km，断层宽度10km，计算库仑应力需要有断层面以及滑动方向，假设接收点处的断层面以及滑动方向与破裂断层一致，计算深度为地下5.0km，接收点横坐标从－20.0km起始，到40.0km截止，共取13个点，纵坐标从20.0km起始，到40.0km截止，共取5个点，首先基于半无限介质模型，介质参数为P波速度6.2km／s，S波速度3.5km／s，密度2.9g／cm3，分别根据Okada［12－13］和本文的方法计算库仑应力变化.图7a分别给出了相应的计算结果，以及绝对误差，由图可见两者误差很小，再次验证了数值计算的精度.考虑分层介质模型（表2），计算得到库仑应力分布，图7b给出其与半无限结果的比较图，两者在库仑应力大小上存在着显著差异，因此在计算应力触发时，考虑分层弹性半无限介质模型是有必要的.

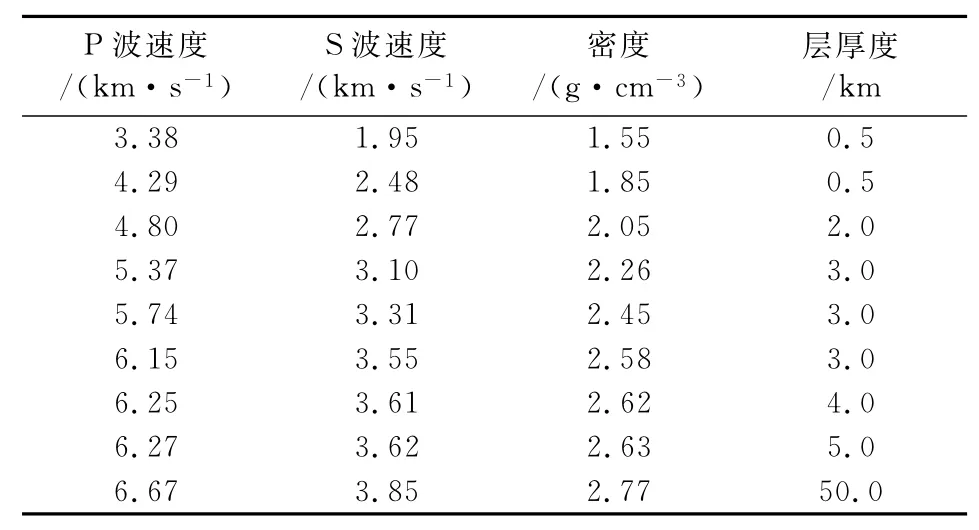
表2 速度结构模型Table 2 The velocity model

图3 均匀弹性半无限介质中，接收点位于地表时，位移、应力结果比较（a）位移结果比较，横坐标为接收点位置，纵坐标为位移大小，左、中、右分别对应于X、Y和Z方向位移，上、中、下分别对应于走滑、倾滑和拉张断层，其中方框为Okada给出的解析解结果，圆点为本文程序给出的计算结果；（b）应力结果比较，横坐标为接收点位置，纵坐标为应力张量各分量大小，左、中、右分别对应于走滑、倾滑和拉张断层，上对应于正应力，其中曲线为Okada给出的解析解结果，圆点为本文程序给出的计算结果.黑色为X向正应力，灰色为Y向正应力，下为两者之间的剪切应力.Fig.3 The displacement and stress in the half－space model，the receiver is in the surface（a）The comparison of displacement results，the X－axis shows the location of the receiver，Y－axis shows the displacement，the left，middle，right columns represent the displacements of X，Y，Zcomponent respectively，the upper，middle，lower lines represent the strike－slip，dipslip，tensile sources respectively，the squares show the analytical solutions，the points show the results of our method；（b）The comparison of stress results，the X－axis shows the location of the receiver，Y－axis shows the stress，the left，middle，right columns represent the strike－slip，dip－slip，tensile sources respectively，the upper lines show the analytical solutions，the points show the results of our method，black，gray represent the normal stress ofX，Ycomponent respectively and the lower lines represent the shear stress.

图4 均匀弹性半无限介质中，接收点位于地下，深度小于震源深度时，位移、应力结果比较（a）位移结果比较，横坐标为接收点位置，纵坐标为位移大小，左、中、右分别对应于X、Y和Z方向位移，上、中、下分别对应于走滑、倾滑和拉张断层，其中红色方框为Okada给出的解析解结果，蓝色圆点为本文程序给出的计算结果；（b）应力结果比较，横坐标为接收点位置，纵坐标为应力张量各分量大小，左、中、右分别对应于走滑、倾滑和拉张断层，其中直线为Okada给出的解析解结果，圆点为本文程序给出的计算结果.上半部分为正应力，黑、红、蓝色分别表示X、Y和Z方向的正应力，下半部分为剪切应力，黑、红、蓝色分别表示XY、XZ和YZ方向的剪切应力.Fig.4 The displacement and stress in the half－space model，the receiver is underground and the depth of it is above that of the source（a）The comparison of displacement results，the X－axis shows the location of the receiver，Y－axis shows the displacement，the left，middle，right columns represent the displacements of X，Y，Zcomponent respectively，the upper，middle，lower lines represent the strike－slip，dip－slip，tensile sources respectively，the red squares show the analytical solutions，the blue points show the results of our method；（b）The comparison of stress results，the X－axis shows the location of the receiver，Y－axis shows the stress，the left，middle，right columns represent the strike－slip，dip－slip，tensile sources respectively，the upper，lower lines represent the normal，shear stress respectively，in the normal stress，black，red，blue represent the normal stress ofX，Y，Zcomponent respectively，in the shear stress，black，red，blue represent the shear stress of XY，XZ，YZcomponent respectively.

图5 均匀弹性半无限介质中，接收点位于地下，深度大于震源深度时，位移、应力结果比较（a）位移结果比较，横坐标为接收点位置，纵坐标为位移大小，左、中、右分别对应于X、Y和Z方向位移，上、中、下分别对应于走滑、倾滑和拉张断层，其中红色方框为Okada给出的解析解结果，蓝色圆点为本文程序给出的计算结果；（b）应力结果比较，横坐标为接收点位置，纵坐标为应力张量各分量大小，左、中、右分别对应于走滑、倾滑和拉张断层，其中直线为Okada给出的解析解结果，圆点为本文程序给出的计算结果.上半部分为正应力，黑、红、蓝色分别表示X、Y和Z方向的正应力，下半部分为剪切应力，黑、红、蓝色分别表示XY、XZ和YZ方向的剪切应力.Fig.5 The displacement and stress in the half－space model，the receiver is underground and the depth of it is blow that of the source（a）The comparison of displacement results，the X－axis shows the location of the receiver，Y－axis shows the displacement，the left，middle，right columns represent the displacements of X，Y，Zcomponent respectively，the upper，middle，lower lines represent the strike－slip，dip－slip，tensile sources respectively，the red squares show the analytical solutions，the blue points show the results of our method；（b）The comparison of stress results，the X－axis shows the location of the receiver，Y－axis shows the stress，the left，middle，right columns represent the strike－slip，dip－slip，tensile sources respectively，the upper，lower lines represent the normal，shear stress respectively，in the normal stress，black，red，blue represent the normal stress of X，Y，Zcomponent respectively，in the shear stress，black，red，blue represent the shear stress of XY，XZ，YZcomponent respectively.

图6 均匀弹性水平层状介质中，接收点位于地表时的位移、应力结果比较（a）位移结果比较，横坐标为接收点位置，纵坐标为位移大小，左、中、右分别对应于X、Y和Z方向位移，上、下分别对应于走滑、倾滑断层，其中方框为Wang et al.（2003）［17］给出的结果，圆点为本文程序给出的计算结果；（b）应力结果比较，横坐标为接收点位置，纵坐标为应力张量各分量大小，左、右分别对应于走滑、倾滑断层，上对应于正应力，其中曲线为Wang et al.（2003）［17］给出的结果，圆点为本文程序给出的计算结果.黑色为X向正应力，灰色为Y向正应力，下为两者之间的剪切应力.Fig.6 The displacement and stress in the layered velocity model，the receiver is in the surface（a）The comparison of displacement results，the X－axis shows the location of the receiver，Y－axis shows the displacement，the left，middle，right columns represent the displacements of X，Y，Zcomponent respectively，the upper，lower lines represent the strike－slip，dip－slip sources respectively，the squares show the solutions of Wang et al.（2003）［17］，the points show the results of our method；（b）The comparison of stress results，the X－axis shows the location of the receiver，Y－axis shows the stress，the left，right columns represent the strike－slip，dip－slip sources respectively，the upper lines represent the normal stress，the lines show the solutions of Wang et al.（2003）［17］，the points show the results of our method，black，gray represent the normal stress of X，Ycomponent respectively and the lower represent the shear stress the shear stress.

图7 库仑应力比较（a）半无限介质解析解与本文计算结果比较，左、中、右分别为解析解、本文结果以及误差绝对值；（b）半无限介质与分层介质结果比较，左、中、右分别为半无限介质结果、分层介质结果以及误差绝对值.Fig.7 The Coulomb stress（a）The results of analytical and our method in the half－space model，the left，middle，right columns represent the analytical solution，result of our method and absolute value of discrepancy between them respectively；（b）The comparison of the half－space model and layered model，the left，middle，right columns represent the solution in the half－space，result in the layered model and absolute value of discrepancy between them respectively.

表3 不同积分方式的计算结果比较Table 3 Comparison of different integration methods

5 同震位移计算中积分方式的比较

为了提高同震位移的计算速度，利于反演问题研究，我们改进了积分方式.通过不同的积分方法计算了半无限介质模型中点源产生的同震位移，考察了改进方式的优越性.接收点设定于地表，坐标为（20km，250km）.震源参数设定为：震源深度7.0km，断层面积0.01km×0.01km，倾角为60°.

由计算结果（表3）可见，采用改进的积分方式（积分方式二）计算同震位移时，核函数计算次数减少了2／3左右，而误差均控在3%以内.这样既保证了计算精度，又提高了计算速度，有利于反演问题研究.

6 结 论

本文进一步发展了基于均匀弹性水平层状介质，利用广义反射透射系数矩阵和离散波数计算同震位移的方法［29－30］，使之可以计算相应的应变、应力以及同震库仑应力变化.接收点可以位于地表以及地下，可以适应于剪切位错源和拉张源等.根据应力张量计算同震库仑应力的变化，可用于地震触发研究，为判断余震分布提供参考.谢小碧和姚振兴［29］，He等［30］计算同震位移时，均采用了简单的梯形积分方式，本文使用了梯形积分与Filon积分相结合的积分方式，既提高了同震位移计算的速度，又保证了计算精度，有利于反演问题研究.

（References）

［1］ Stein R S，King G C P，Lin J.Change in failure stress on the southern San Andreas fault system caused by the 1992 magnitude＝7.4Landers earthquake.Science，1992，258（5086）：1328－1332.

［2］ Bouchon M.The state of stress on some faults of the San Andreas system as inferred from near－field strong motion data.J.Geophys.Res.，1997，102（B6）：11731－11744.

［3］ 沈正康，万永革，甘卫军等.东昆仑活动断裂带大地震之间的黏弹性应力触发研究.地球物理学报，2003，46（6）：786－795.Shen Z K，Wan Y G，Gan W J，et al.Viscoelastic triggering among large earthquakes along the east Kunlun fault system.Chinese J.Geophys.（in Chinese），2003，46（6）：786－795.

［4］ King G C P，Stein R S，Lin J.Static stress changes and the triggering of earthquakes.Bull.Seism.Soc.Am.，1994，84（3）：935－953.

［5］ 石耀霖，曹建玲.库仑应力计算及应用过程中若干问题的讨论—以汉川地震为例.地球物理学报，2010，53（1）：102－110.Shi Y L，Cao J L.Some aspects in static stress change calculation—case study on Wenchuan earthquake.Chinese J.Geophys.（in Chinese），2010，53（1）：102－110.

［6］ Toda S，Stein R S，Reasenberg P A，et al.Stress transferred by the 1995 Mw＝6.9Kobe，Japan，shock：effect on aftershocks and future earthquake probabilities.J.Geophys.Res.，1998，103：24543－24565.

［7］ 万永革.“地震静态应力触发”问题的研究.北京：中国地震局地球物理研究所，2001.Wan Y G.The study about“Static stress triggering”（in Chinese）.Beijing：Institute of Geophysics China Earthquake Administration，2001.

［8］ Barka A.The 17August 1999Izmit earthquake.Science，1999，258（5435）：1858－1859.

［9］ Steketee J A.On volterra′s dislocations in a semi－infinite elastic medium.Can.J.Phys.，1958，36（2）：192－205.

［10］ Maruyama T.Static elastic dislocation in an infinite and semiinfinite medium.Bull.Earthquake Res.Inst.Tokyo Univ.，1964，42：289－368.

［11］ Press F.Displacements，strains，and tilts at teleseismic distances.J.Geophys.Res.，1965，70（10）：2395－2412.

［12］ Okada Y.Surface deformation due to shear and tensile faults in a half－space.Bull.Seism.Soc.Am.，1985，75（4）：1135－1154.

［13］ Okada Y.Internal deformation due to shear and tensile faults in a half－space.Bull.Seism.Soc.Am.，1992，82：1018－1040.

［14］ Sato R，Matsu′ura M.Static deformations due to the fault spreading over several layers in a multilayered medium，I，displacement.J.Phys.Earth，1973，21（3）：227－249.

［15］ Ben－Menahem A，Singh S J.Multipolar elastic fields in a layered half space.Bull.Seism.Soc.Am.，1968，58（5）：1519－1572.

［16］ Singh S J.Static deformation of a multilayered half－space by internal sources.J.Geophys.Res.，1970，75（17）：3257－3263.

［17］ Wang R，Martin F L，Roth F.Computation of deformation induced by earthquakes in a multi－layered elastic crust：FORTRAN programs EDGRN／EDCMP.Comp.Geosci.，2003，29（2）：195－207.

［18］ Israel M，Ben－Menahem A，Singh S J.Residual deformation of real Earth models with application to the Chandler wobble.Geophysical Journal of the Royal Astronomical Society，1973，32（2）：219－247.

［19］ Pollitz F F.Coseismic deformation from earthquake faulting on a layered spherical earth.Geophys.J.Int.，1996，125（1）：1－14.

［20］ Nur A，Mavko G.Postseismic viscoelastic rebound.Science，1974，183（4121）：204－206.

［21］ Wang R，Martin F L，Roth F.PSGRN／PSCMP—a new code for calculating co－and post－seismic deformation，geoid and gravity changes based on the viscoelastic－gravitational dislocation theory.Comp.Geosci.，2006，32（4）：527－541.

［22］ Pollitz F F.Postseismic relaxation theory on the spherical earth.Bull.Seism.Soc.Am.，1992，82（1）：422－453.

［23］ Masterlark T，Wang H F.Transient stress coupling between the 1992Landers and 1999Hector Mine，California，earthquakes.Bull.Seism.Soc.Am.，2002，92（2）：1470－1480.

［24］ 张怀，吴忠良，张东宁等.虚拟川滇—基于千万网格并行有限元计算的区域强震演化过程数值模型设计和构建.中国科学D辑，2009，39（3）：260－270.Zhang H，Wu Z L，Zhang D N，et al.Quasi Sichuan－Yunnan－Based on thousands of grid parallel finite element computations strong earthquake evolution process numerical model design and construction.Science Chian（D）（in Chinese），2009，39（3）：260－270.

［25］ Kennett B L N.Reflections，rays，and reverberations.Bull.Seism.Soc.Am.，1974，64（6）：1685－1696.

［26］ Kennett B L N.Seismic wave propagation in stratified media.New York：Cambridge U.Press，1983.

［27］ Bouchon M.Discrete wave number representation of elastic wave fields in three－space dimensions.J.Geophys.Res.，1979，84（B7）：3609－3614.

［28］ Yao Z X，Harkrider D G.A generalized reflection transmission coefficient matrix and discrete wavenumber method for synthetic seismograms.Bull.Seism.Soc.Am.，1983，73（6A）：1685－1699.

［29］ 谢小碧，姚振兴.计算分层介质中位错点源静态位移场的广义反射、透射系数矩阵和离散波数方法.地球物理学报，1989，32（3）：270－280.Xie X B，Yao Z X.A generalized reflection－transmition coefficient matrix method to calculate static displacement field of a stratified half－space by dislocation source.Chinese J.Geophys.（in Chinese），1989，32（3）：270－280.

［30］ He Y M，Wang W M，Yao Z X.Static deformation due to shear and tensile faults in a layered half－space.Bull.Seism.Soc.Am.，2003，93（5）：2253－2263.

［31］ Mallick S，Frazer L N.Practical aspects of reflectivity modeling.Geophysics，1988，55（10）：1355－1364.

［32］ 纪晨，姚振兴.区域地震范围的宽频带理论地震图算法研究.地球物理学报，1995，38（4）：460－468.Ji C，Yao Z X.The study of the method for broadband regional synthetic seismogram.Chinese J.Geophys.（in Chinese），1995，38（4）：460－468.

［33］ Chen X F，Zhang H M.An efficient method for computing Green′s functions for a layered half－space at large epicentral distances.Bull.Seism.Soc.Am.，2001，91（4）：858－869.

［34］ Cotton F，Coutant O.Dynamic stress variations due to shear faults in a plane－layered medium.Geophys.J.Int.，1997，128（3）：676－688.

［35］ Aki K，Richards P G.Quantitative Seismology：Theory and Methods.San Francisco：W.H.Freeman and Co.，1980.

［36］ 汪建军.同震、震后和震间应力触发.武汉：武汉大学，2010.Wang J J.Coseismic，Postseismic and Interseismic Stress Triggerings（in Chinese）.Wuhan：Wuhan University，2010.

［37］ 周宇明，单斌，熊熊.静态应力触发中影响库仑应力变化的参数敏感性分析.大地测量与地球动力学，2008，28（5）：21－26.Zhou Y M，Shan B，Xiong X.Parameters sensitivity analysis of Coulomb stress change in static stress triggering.Journal of Geodesy and Geodynamics（in Chinese），2008，28（5）：21－26.

The coseismic displacement，strain and stress in the layered elastic model

HAO Jin－Lai，YAO Zhen－Xing
Institute of Geology and Geophysics，Chinese Academy of Sciences，Beijing100029，China

The coseismic displacement，strain and stress，especially the change of the coseismic stress，are significant in the earthquake triggering investigation.Based on the layered elastic model，we develop a method to calculate the coseismic dislocation by the generalized reflectiontransmission coefficient matrix and discrete wavenumber method.We can use it to calculate the coseismic strain，stress，and the change of Coulomb stress.It can be applied in the general situation.The receiver can be located on the surface or underground.The earthquake source can be pure shear dislocation source or tensile source.For the half－space model，the result of our method coincides with the analytical solution，so the precision of our method is reliable.The method can be used to calculate the Coulomb stress after an earthquake，and the change of Coulomb stress can give a reference to estimate the distribution of the aftershocks.We combine the trapezoidal integration method with the Filon integration method to calculate the coseismic displacement.It improves the speed of the calculation and there is no accuracy loss.It is useful for the inversion research based on the coseismic displacement.

Generalized reflection－transmission coefficient matrix，Discrete wavenumber，Coseismic displacement，Coulomb stress，Layered elastic model

10.6038／j.issn.0001－5733.2012.05.025

P315

2011－04－23，2012－03－28收修定稿

国家重点基础研究发展计划（2008CB425701）和国家自然科学基金（40974028；41030319）资助.

郝金来，男，1984年生，理学博士，主要从事震源机制与同震形变等方面的研究.E－mail：haojinlai＠gmail.com

郝金来，姚振兴.均匀弹性分层介质模型中的同震位移、应变以及应力.地球物理学报，2012，55（5）：1682－1694，

10.6038／j.issn.0001－5733.2012.05.025.

Hao J L，Yao Z X.The coseismic displacement，strain and stress in the layered elastic model.Chinese J.Geophys.（in Chinese），2012，55（5）：1682－1694，doi：10.6038／j.issn.0001－5733.2012.05.025.

（本文编辑 胡素芳）