同步轨道共位卫星位置确定技术

胡 娟，陈文全

(1.郑州航空工业管理学院电子通信工程系，河南郑州 450047;2.中国电子科技集团公司第27研究所测控部，河南郑州 450015)

地球同步轨道卫星具有相对地球为“静止”的特点，可以有效地利用其为通讯、数据传输、电视广播、气象、海洋探测、导航和军事等行业和科学研究服务，并已发挥显著的应用价值和经济价值。截至2005年，地球同步轨道附近约60 km宽的区域内共有卫星1 120个［1］。随着各国对同步轨道卫星需求的增加，同步轨道位置日趋紧张，提高地球同步轨道弧段利用率越来越受重视。

同步轨道多星共位可以解决同步轨道卫星需求的增长，可以提高地球同步轨道弧段利用率。所谓“多星共位”，就是在东西、南北方向均为±0.1°窗口放置两颗或两颗以上同步卫星［2］。20世纪80年代末到90年代初，ESA的Olympus通信卫星和德国一颗、法国两颗卫星共位运行［3］。1992年德国科学家提出了在同一轨道窗口内放置7颗同步卫星的方案设想。为避免卫星飘出共位窗口，需要对窗口内的卫星确定绝对位置;为提高同一个窗口的卫星数量，避免卫星间发生碰撞，需要精密测量卫星间的相对位置。

1 共位卫星位置确定原理

目前，国内同步轨道卫星绝对位置高精度确定主要采用相距几千公里的多个测量站，通过双边距离转发测量目标到各测量站的距离进行定位。星群、星座等卫星间的相对位置主要采用星间微波、激光测量方式。双边距离转发测量同步卫星的绝对位置，各测量站距离太远，不利于满足共视条件和安排观测任务。星间微波、激光测量方式需要星上装载测量设备，已经在轨的卫星不能实现。下面介绍一差分连接端站干涉技术(CEI)，可以同时实现同步轨道共位卫星绝对位置和相对位置测量。

CEI属于角度测量系统，可用于航天器的导航测量。两个地面站被动接收同一个无线电信号源，参照共同的参考频率得两站所收信号的相位差，由此导出信号源到两站的距离差(DOR)，结合两站的高精度基线长度，从而获得导航所需的信号源至基线的方向角θ，利用两条非平行的基线可以测得飞行器的两个方向角的测量值［8］，如图1所示。对于共位卫星的测量可以增加一个测距信息，如采用一主两副的CEI系统，主站发出上行信号，通过共位卫星转发后，主站和两个副站同时接收转发下来的信号。一方面主站通过收发信号的时延，得到主站到共位卫星的距离R;另一方面，通过比较主副站接收信号的相位延迟，得到共位卫星到主副站的距离差r，从而形成Rr1r2测量体制。该测量体制要求站间基线不能过长，站间要求有同一时钟参考频率，或要求较高的时钟同步精度。

图1 CEI测量原理示意图

采用CEI对同步卫星的绝对位置测量由于存在基线、对流层、电离层、时钟等误差，测量精度较低。可以采用差分CEI测量技术，抵消各种测量误差，提高测量精度。差分CEI工作原理如图2所示，测量差分单向差分距离ΔDOR和差分单向多普勒ΔDOD。

图2 差分CEI观测原理示意图

设C为光速;R1A和R2A为射电星到测控站1和测控站2的单向距离;R1B和R2B为航天器到测控站1和测控站2的单向距离;τc1、τc2为测控站1和测控站2的时钟误差;τS1A、τS2A、τS1B、τS2B为射电星和卫星 B 至测控站1和测控站2由大气、等离子等介质差引入的传输时延误差;τd1A、τd1B、τd2A、τd2B为测控站 1、测控站 2 接收航天器A、B的接收设备时延。

射电星至测控站1和测控站2的距离测量值ρ1A、ρ2A分别为

航天器至测控站1和测控站2的距离测量值ρ1B、ρ2B分别为

目标A到两测量站的距离差DORA为

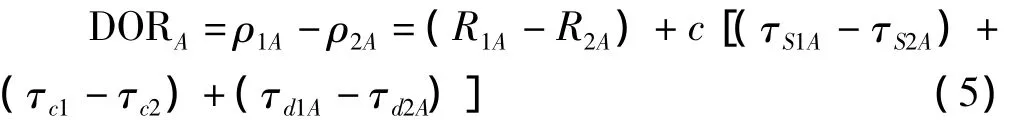
同理，

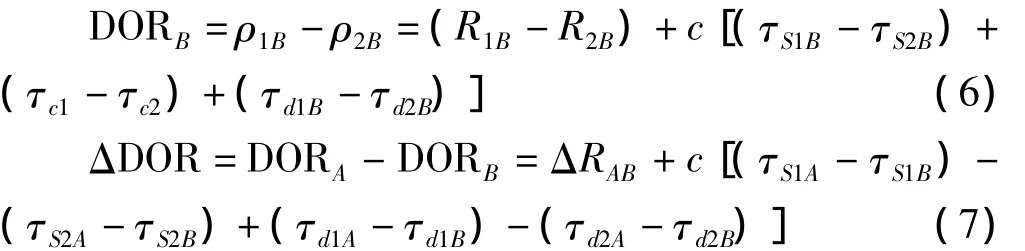
其中，ΔRAB=(R1A－R2A)－(R1B－R2B)为两个目标到两个测控站的差分距离差真值。如图，航天器和射电星形成的夹角 α、β 小于 10°时，存在 τS1A≈τS1B，τS2A≈τS2B。这样，大部分误差通过差分抵消，提高了测量精度

差分多普勒ΔDOD为差分单向差分距离对时间求导

采用射电星校正，约20 km基线的CEI系统，航天器角度测量精度可达70 nrad［7］。采用射电星校正虽然测量精度高，但是由于射电星信号微弱，需要面积较大的天线，成本较高，且转动不灵活。目前，国际上也在研究没有射电源校准的CEI系统，其中采用GPS卫星作为校准源是一种较好的方案。这样天线可以做得很小，甚至约1 m的口径就可以工作。基于GPS校准的CEI系统，100 km的基线，测角精度能达到300 nrad以下［6］。

可以通过GPS校准的CEI系统对同步轨道共位卫星绝对位置测量，对同步轨道共位卫星相对位置测量可以采用CEI系统同波束干涉测量。所谓同波束干涉测量(SBI)，就是当两个航天器在角度上非常接近时，它们可以在一个地面天线的同一波束内被观测，使用两个地面站天线对两个航天器同时观测，可以形成差分干涉测量。同波束干涉测量可以提供天平面上非常精确的相对位置测量量，作为对地基多普勒和距离测量视线信息的重要补充［4］。

SBI测量原理和差分CEI测量原理一样，也是测量差分单向差分距离(ΔDOR)和差分单向多普勒(ΔDOD)，仅仅是测量的两个目标更近，两个目标可以在同一个波束内，可以同时测量两个目标，不需要天线切换。同步轨道卫星在±0.1°窗口内，两颗卫星和测站的夹角＜0.2°，目标可以落在天线的同一波束内，测控站对两个航天器信号同时观测，采用相同的时钟频率，时钟误差可以抵消。航天器信号如果频率相近，可以采用宽带接收设备同时接收，设备误差仅存在群时延不一致性误差，其它误差几乎全部抵消。通过SBI测量，可以高精度确定同步轨道卫星间的相对位置。

2 共位卫星位置测量精度分析

2.1 共位卫星绝对位置测量精度分析

同步轨道共位卫星绝对位置测量采用100 km基线的GPS校正CEI系统测量，CEI定位采用Rlm定位体制，目标的位置坐标(x，y，z)为

其中，l、m、n为3个方向上的方向余弦;R为目标到测量站的距离。

假设各个方向上的误差一致，对式(9)求偏导，然后经过推倒，CEI定位精度公式经推导可用式(10)表示

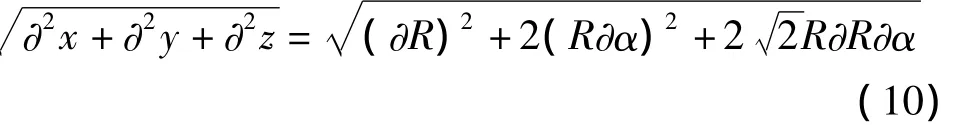
其中，∂R为测站测量航天器的距离误差;R为测站到航天器的距离，取50 000 km，∂α为CEI方向余弦角误差。采用GPS校正的CEI系统对同步轨道共位卫星进行绝对位置测量，根据文献［6］可知，方向余弦角度测量可以优于300 nrad。目前，测量站测距精度系统误差优于2 m，随机误差优于1 m，传播路径误差经修正后一般是m量级，所有测距误差的均方和＜10 m。按照上述条件，定位误差约为31.21 m。

2.2 共位卫星相对位置测量精度分析

甚长基线干涉测量(VLBI)系统是目前测量精度最高的测量系统，采用甚长基线干涉测量系统，同波束干涉测量精度经过分析可达36 prad［5］，满足同步轨道共位卫星相对位置精度需求。但VLBI测量需要远程传输，不能实时处理，并且安排观测比较困难。这里采用CEI系统分析同步轨道共位卫星相对位置的测量精度。

文献［5］对深空探测SBI测量差分相对距离误差进行了详尽的分析。误差源包括太阳等离子体、电离层、对流层等引起的传输时延误差，系统噪声、相位漂移、航天器晶振漂移、未校准群时延或时钟偏差引起的地面站测量误差，基线误差引起的测量误差。同步轨道卫星是近地卫星，金星、火星等太阳行星旁航天器目标不同，它受太阳等离子体影响很小，可以或略不计。

同步轨道卫星是高轨卫星，离地面约36 000 km，CEI测量的各个测量站对卫星观测的仰角都很高，这里分析取测量站仰角为45°。并不是所有同步轨道卫星都采用双频传输，这里分析取C频段单频进行分析，天线口径10 m，积分时间1 s。单频电离层影响较大，可以通过GPS长期观测同步轨道共位卫星方向的电离层影响。通过GPS观测，C频段天顶方向电离层影响可以降低到30 mm以下。对流层和频率没有关系，可以采用GPS掩星观测，对流层天顶方向影响可以降低到40 mm以下。如果采用微波辐射计校准，精度更高。根据上述条件，采用文献［5］的分析方法，同步轨道共位卫星SBI测量差分相对距离误差表1所示。

表1 差分相对距离误差

两目标相对位置可以通过式(9)分别计算出两个目标的位置，对其作差，获得其相对位置。对相对位置中距离、方向余弦角等变量求偏导。假设各个方向余弦误差相同，通过化简计算得到相对位置误差为

其中，xAB，yAB，zAB是 A、B 两个航天器 x，y，z位置坐标差。假设单站测距精度系统误差为2 m，随机误差δR为1 m。由于系统差可以在定轨过程中扣除，这里计算精度按照随机测距误差计算。δRAB= δRA－ δRB，δRA和δRB为测站测量航天器A和航天器的距离随机差。RA为测站到航天器A的距离，ΔR为测站到航天器A距离和航天器B距离的差，δαAB为SBI方向余弦角误差，δα为系统测量单个目标的方向余弦角误差。

根据前面分析，基线100 km，方向余弦角45°，δα取300 nrad，δαAB为 3.6 nrad。取 RA为 50 000 km，ΔR＜300 m，取值300 m。通过 CEI系统进行 SBI测量，相对位置误差约为1.5 m。对于10 km的基线，误差最大放大10倍，相对位置也可达＜15 m。

3 结束语

同步轨道卫星用途广泛，“多星共位”可以解决同步轨道卫星日益增长的需要。通过分析可以看出，采用CEI系统进行同步轨道共位卫星位置确定，100 km的基线，采用GPS校正绝对位置定位精度＜50 m。采用SBI技术测量它们间的相对位置，相对位置定位精度可以达到m级。要达到同样的测量精度，传统的测距、多普勒跟踪测量需要几个小时甚至几天的时间。而采用测距和连接端站干涉测量相结合，航天器三维位置可以在直接测定，能够满足同步轨道共位卫星高精度测量的要求。

［1］郑军，陈宏.GEO卫星寿命末期离轨控制策略［J］.上海航天，2007(3):38－41.

［2］李果.同步轨道多星共位轨道保持技术研究［J］.航天控制，1997(3):73－80.

［3］STTDEN L A.地球静止轨道手册［M］.王正才，译.北京:国防工业出版社，1999.

［4］CATHERINE L，THORNTON J SB.深空导航无线电跟踪测量技术［M］.李海涛，译.北京:清华大学出版社，2005.

［5］FOLKNER W M，BORDER J S.Orbiter－ orbiter and orbiter－lander tracking using same－beam inteiferometry［R］.Taipei:TDA Progress Report 42 －109，1992.

［6］闫春生.基于GPS校准的CEI系统测量原理和精度分析［J］.电讯技术，2003(4):20 －24.

［7］THURMAN S W.Information content of a single pass of phase－delay data from a short baseline connected element interferometer［R］.Taipei:TDA Progress Report，1990.

［8］董光亮.BRT和CEI技术用于数据中继卫星.测定轨的分析比较［J］.飞行器测控学报，2004，23(1):6－10.