利用地球简正模耦合研究上地幔过渡区方位各向异性

胡小刚，薛秀秀，郝晓光

中国科学院测量与地球物理研究所，大地测量与地球动力学国家重点实验室，武汉 430077

利用地球简正模耦合研究上地幔过渡区方位各向异性

胡小刚，薛秀秀，郝晓光＊

中国科学院测量与地球物理研究所，大地测量与地球动力学国家重点实验室，武汉 430077

地震方位各向异性广泛存在于地球上地幔中，目前利用地震体波或面波分析研究上地幔各向异性的地球物理方法有很多种，但是由于各自的局限性均难以分析上地幔过渡区中的各向异性特征.方位各向异性可导致球形简正模和环形简正模之间发生耦合.地球长周期自由振荡的简正模可深入到上地幔过渡区.本文利用各向异性地球模型计算各向异性简正模耦合深度敏感核，表明长周期（250～400s）简正模各向异性耦合（如0S20－0T21和0S25－0T25）的敏感度峰值在400～600km之间.在不受地球自转影响的台站，如位于南极极点的QSPA站，仍然可以观测到强烈的简正模耦合现象.本文的研究表明：只有在地震观测台站靠近长周期球形振荡的节点时，才能在其观测数据中观测到各向异性耦合现象，许多各向异性耦合在震后18～24h期间最强，并可导致垂直方向的环形简正模的振幅大于球形耦合简正模的振幅.这些特征是在地震观测数据中寻找各向异性耦合的重要线索.长周期简正模的方位各向异性耦合为我们提供了一个新的认识上地幔过渡区各向异性的窗口.

地球自由振荡，简正模耦合，上地幔过渡区，方位各向异性

1 引 言

地震各向异性（seismic anisotropy）是地球内部各向异性介质对地震波传播的影响，其表现为地震波的传播速度的大小与其传播方向有关.构成地球的介质晶粒在随机无序地排列后，地球介质在宏观上表现为各向同性.但地球内部的动力可导致地球介质有序地排列，使其表现出各向异性的特征.总体而言，产生各向异性的因素可分为两类，一类为岩层中构造的特定排列引起的各向异性，称之为SPO（Shape－Preferred Orientation）各向异性，例如岩石中由于应力作用而引起的裂隙定向排列，造成岩石圈中的各向异性.另一类为岩石晶粒根据应变环境沿特定方向排列引起的各向异性，称之为LPO（Lattice－Preferred Orientation）各向异性，例如岩石圈冷却过程中应力作用、软流圈或地幔对流中的物质形变会引起橄榄岩中晶格的定向排列，造成地壳和地幔中出现大规模的各向异性.

观测和分析地震体波或面波通过各向异性介质时速度和性质的变化可研究地球内部的各向异性.地震体波的变化表现为：Pn波速度随传播方向变化、P－S波转换随方向变化、剪切波分裂.地震面波的变化表现为：Love－Rayleigh差异（L－R discrepancy）、方位各向异性、偏振异常.

Pn波是沿近水平方向传播的纵波.Pn波由震源发出后，沿莫霍界面传播滑行一段，再传播到地表.Hess[1]首次观测到Pn波的方位各向异性，确定壳幔边界存在各向异性.但Pn波速度各向异性只能证明上地幔顶部存在径向各向异性.

径向各向异性可导致部分P波转换为S波，形成Ps转换波震相.P－S转换主要出现在速度间断面上.间断面处的径向各向异性能加强P波转换为S波，形成Ps震相，还能根据入射波的角度改变Ps波的振幅，由此可区别各向异性的强度和对称轴[2－4].

剪切波分裂是指线性偏振剪切波通过各向异性介质会分裂为偏振方向相互垂直的快波和慢波[5].剪切波的快波极化方向及快慢波的分裂时间可反映各向异性介质的特征[6－7]，其中远震SKS分裂提供的存在各向异性的信息最为可靠[8]，但观测SKS分裂不能确定地幔各向异性区域的深度范围，无法分辨多层各向异性的情况[9].

L－R discrepancy是剪切波各向异性效应在面波上的体现，表现为由Rayleigh波反演得到的S波径向速度VSV与Love波反演得到的S波水平速度VSH之间存在差异.介质径向各向异性是导致L－R discrepancy的主要原因[10].

介质的方位（横向）各向异性导致面波沿不同方位传播时其速度不同.分析面波速度层析成像可获得介质方位各向异性的特征信息.由于不同波长的面波在不同深度的球面上传播，面波层析成像可以定位各向异性的深度范围.

地震面波通过方位各向异性介质时会产生偏振异常现象.线性极化的Love波转化为椭圆极化的Rayleigh波——Quasi－Love波；Rayleigh波转化为线性极化的 Love波——Quasi－Rayleigh波[11－12].能否观测到长周期Quasi－Love波 （70～100s）是判断上地幔（深度范围100～300km）中存在方位各向异性的重要证据之一[13].

面波速度层析成像、剪切波分裂、P－S波转换、面波偏振异常是目前探测地震各向异性4种主要手段.但直接采用这些手段探测上地幔过渡区中的方位各向异性，则显得比较困难.因为高频地震面波不能进入到上地幔过渡区，而远震体波纵向分辨率低，无法分辨各向异性的径向分布情况.

2 上地幔过渡区中的各向异性

上地幔过渡区位于上下地幔中间，是介于410km和660km两个地震波速度间断面之间的构造.上地幔过渡区在地幔动力学活动中扮演着重要角色.尤其是660km间断面，极有可能起到约束着上下地幔之间的物质通道的作用[14].目前对地球内部热演化和化学演化的推断主要依赖于了解上地幔过渡区的形成方式；上地幔过渡区的形成究竟是由于压力形成的阶段变化，还是由于矿物成分改变的长期变化，或是二者兼有[15].认识上地幔过渡区中各向异性特征及其分布可为研究板块俯冲，地幔对流，乃至整个地球的动力学形态提供必要的约束和参考.

直接利用现有的手段和方法观测和分析地球上地幔过渡区各向异性比较困难.但有不少间接证据表明上地幔过渡区中存在各向异性.例如：Montagner和Kennett[16]在分析体波走时观测结果和体波走时理论结果的差异时，指出在地球660km间断面应该存在径向各向异性；Vinnik[17－18]用各向异性地球模型分析研究P－S转换观测结果和SKS分裂观测结果的差异时，表明在观测台站下方660km间断面附近存在方位各向异性.Fouch和Fischer[19]在研究太平洋俯冲带地幔各向异性时，用S波和远震SKS分裂的观测数据匹配各向异性模型，表明在过渡带400～520km范围存在方位各向异性.Wookey等[20]在 Tonga－Kermadec和 New Hebrides俯冲带观测到了深层地震S波分裂时间长达7s，指出在台站下方660km间断面极有可能存在方位各向异性，并推测上地幔过渡区对上下地幔之间的物质流动可能会起到阻碍作用.

Trampert和 Heijst[21]证明Love波的谐频波（overtone）对上地幔过渡区深度的方位各向异性弹性参数（G和E）非常敏感，通过反演Love谐频波（43～153s）的频散，首次给出了地幔过渡区的方位各向异性的全球空间分布.但是他们的计算没有排除上地幔各向异性引起的面波偏振异常[13]，上地幔各向异性介质可导致部分Rayleigh波变为线性极化的 Quasi－Rayleigh波[22].由于很难将 Love波和Quasi－Rayleigh波区分开，Trampert也不得不承认其结果可能存在较大的偏差.

3 地球自由振荡简正模与地震各向异性

地球上发生的大地震可使地球发生整体振动，导致地球的自由振荡.地球的简正模（normal modes）是振荡形成的驻波，其频率是一些固有的离散值.每个简正模称之为一个单谱（singlet），其频率用nωlm表示.其中n表示驻波基频的泛频数，l为角序数，m为方位角序数（m＝－l，－l＋1，… ，0，…，l－1，l）.具有相同n和l值的单谱称为一组多谱（multiplet）.对于球对称、非自转、各向均匀的分层弹性地球模型，一组多谱中的2l＋1个单谱频率简并为相同的频率，简并频率用nωl表示.真实地球的自转、椭率、非均匀、各向异性都会使单谱频率偏离简并频率，产生简正模的分裂现象.地球简正模按其振动方式分两种，球形简正模nSl和环形简正模nTl.nSl是Rayleigh波的驻波，质点的振动位移是在在垂直平面中的椭圆运动，地震仪只能在垂直方向和水平径向记录到nSl信号.nTl是Love波的驻波，质点的振动位移在水平面且垂直于面波的传播方向，因此只有地震仪水平侧向分量可以记录到nTl信号.真实地球的自转、椭率、横向非均匀、各向异性可导致球形简正模与环形简正模发生偏振异常，产生椭圆极化的环形简正模，并导致球形简正模和环形简正模间的耦合（S－T耦合）.这样在地震仪垂直记录方向可记录到环形简正模的信号.在没有S－T耦合情况下，球形简正模垂向振幅谱的观测值与根据地球模型计算得到的简正模振幅谱符合较好.在S－T耦合的影响下，环形简正模出现在垂向振幅谱中且球形简正模的频率和振幅偏离理论值.根据环形简正模垂向振幅的大小可判断S－T耦合的强弱.地球自转对长周期简正模的S－T耦合有很大的影响.理论分析表明在低于3mHz频段，自转可导致球形简正模nSl与环形简正模n′Tl±1的耦合[23－24].地球椭率、密度异常、横向不均匀结构也可导致简正模耦合，但这些因素产生的S－T耦合较弱，其激发的环形简正模垂向振幅的大小不到地球自转激发的1/10[25].

国际上有关上地幔各向异性介质对简正模S－T耦合影响的研究取得了一些重要的结果.Park[26]利用各向异性地球模型研究了地幔中的径向各向异性和方位各向异性对简正模耦合的影响，指出方位各向异性可产生更强的 S－T 耦合.Park和 Yu[11－12]和Oda[27－28]的研究结果表明，地幔中横向非均匀性（横向波速变化率为5%左右）不能产生显著的S－T偶合，而弱方位各向异性（各向异性介质对P波和S波速度扰动小于1.5%左右）能产生显著的S－T耦合.研究结果还显示各向异性S－T耦合的强度与面波的传播方向有关，当传播方向与各向异性对称轴交角为45°时耦合最强，而两者相互平行或垂直时则不能引起耦合[27].长周期各向异性S－T耦合的强度还与参与耦合的驻波节点位置有关，在Rayleigh驻波的节点（Love驻波的腹点）耦合最强，在Love驻波的节点（Rayleigh驻波的腹点）耦合最弱[28].

在地震仪和重力仪的观测数据中，可发现长周期各向异性S－T耦合多发生在频率相近的球形主简正模（fundamental modes）和环形主简正模之间.根据地球分层模型对自由振荡的能量分布进行分析，结果表明长周期（250～400s）球形主简正模的能量集中在上地幔过渡区，但与其耦合的环形简正模的能量主要集中在上地幔（参见图1）.二者的耦合是否对过渡区中的各向异性敏感？我们对此问题进行了分析.

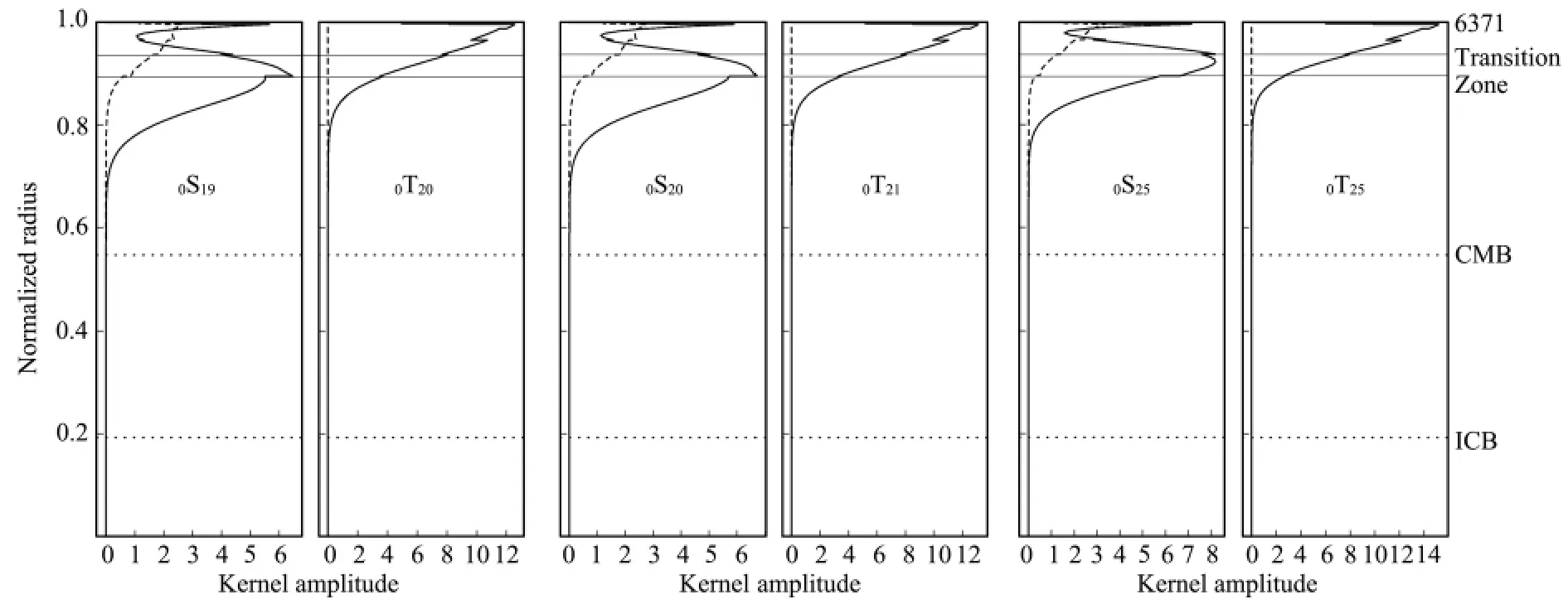
图1 简正模的能量密度分布图Fig.1 Energy densities for normal modes

不考虑密度变化的影响，上地幔方位各向异性和各向同性（横向非均匀性）对P波和S波传播速度的扰动可表示为[29]

其中α和β分别为P波和S波的传播速度，α0和β0分别为P波和S波在横向各向同性地球参考模型中的传播速度.η为地震波传播方向与各向异性对称轴的夹角.B，C，E为各向异性速度扰动参数.A，D为各向同性（横向非均匀性）速度扰动参数.由于Ccos4η很小，参数C的影响通常可忽略不计.

在研究过程中可根据实际情况设定扰动参数A，D，B，C，E，可将其设置为区域性变化，也可设置为全球性变化.例如，若B＝0.009，C＝0.009，E＝0.03，A＝0.0，D＝0.0，相当于在全球不考虑横向不均匀，仅由弱方位各向异性导致0.75%的P波速度扰动和1.5%的S波速度扰动.又如，在上地幔Ccos 4 η较小，P波速度的横向变化和S波的横向变化较为相似，研究全球性问题可做如下假定：其中Rh是深度参数.在这种假定下，各向异性的扰动由参数B和E决定，各向同性的扰动由参数D决定.

利用地球PREM模型[30]和地震波速度扰动方程（1），我们计算了速度扰动参数B、E、D 对S20－0T21和0S25－0T25耦合的影响与各向异性介质深度的关系，即各向异性简正模耦合深度敏感核函数.图2显示耦合对位于深度范围400～660km的方位各向异性速度扰动参数B、E非常敏感，而对横向非均匀性速度扰动参数D不敏感.这一结果表明，如果在重力仪或地震仪垂向分量中能观测到显著的长周期（250～400s）方位各向异性S－T耦合，就可推知方位各向异性介质分布在上地幔过渡区中.

图2 各向异性扰动参数和深度对简正模耦合的影响Fig.2 The influence of anisotropic parameter and depth on normal mode coupling

4 上地幔过渡区各向异性耦合的观测

虽然理论研究表明上地幔方位各向异性可引起简正模S－T耦合，但国际上仅利用T＜150s的耦合观测数据研究上地幔各向异性的分布特征，却一直没有利用长周期简正模耦合观测数据（T＞250s）开展相关的研究工作.其主要原因是地球自转也能导致长周期简正模S－T耦合，没有方法在观测数据中区分自转耦合和各向异性耦合，无法确定能否观测到可靠的长周期各向异性S－T耦合信号.

科里奥利力是导致长周期自由振荡简正模自转耦合的主要原因.在地震面波由震源向两极传播的过程中，Love波的振动受到的科里奥利力最大，这时自转引起的S－T耦合最强.但是，当地震面波沿赤道传播时，Love波的振动方向刚好与地球的自转轴平行，其振动不受科里奥利力的影响，此时自转S－T耦合会消失.2004，2005年苏门答腊大地震的震中紧靠赤道，其激发的地震面波沿非常接近赤道的路径传播到位于赤道附近的地震台.但在靠近赤道的地震台的VHZ记录数据（Very Long Period High Broad Band Z direction甚长周期宽频垂向，采样率0.1sample/s）或LHZ记录数据（Long Period High Broad Band Z direction长周期宽频垂向，采样率1sample/s）中，仍然可以观测到强烈的长周期ST耦合[31]（参见图3）.图3显示赤道地震台ASCN靠近球形振荡0S20的节点，0S20在垂向（vertical）观测数据频谱中的振幅极小，0T21和2T8都出现在垂向记录中，而且其振幅大于0S20的振幅.这些简正模ST强耦合是与地球自转无关的各向异性耦合[31]，表明台站邻近区域下的上地幔过渡区中存在方位各向异性.

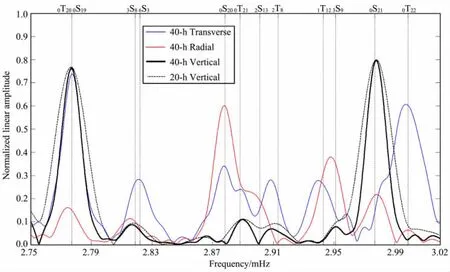
图3 2005－03－28 Mw8.7苏门达腊大地震后赤道地震台ASCN观测数据的振幅谱[31]Fig.3 The amplitude spectra from the station ASCN after the 2005－03－28 Mw8.7Sumatra earthquake[31]

在地球的极区，地球自转科里奥利力很弱，Rayleigh波和Love波的振动几乎不受地球自转的影响，这时地球自转引起的简正模分裂和耦合现象都会减弱乃至消失.我们的观测分析却表明：位于南极极点的地震台QSPA仍然可以在大地震发生后观测 到 显 著 的 S－T 耦 合.图 4 显 示 2004－12－26 Mw9.2苏门答腊大地震后，在18h的QSPA垂向振幅谱中可观测到的0S20与0T21间强烈的耦合.根据震源机制解和地球PREM模型得到的地球自由振荡模拟值显示，QSPA靠近0S20的节线，故其垂向记录中的0S20振幅较小.在地球极点观测到的简正模S－T耦合是与地球自转无关的各向异性耦合，强烈的长周期简正模各向异性耦合表明南极大陆的上地幔过渡区中存在方位各向异性.

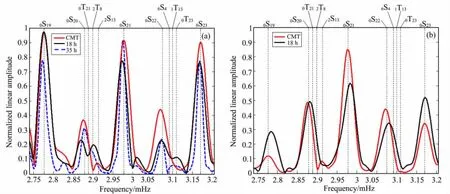
图4 南极地震台QSPA的VHZ观测记录的振幅谱Fig.4 The amplitude spectrum of VHZ from the South Pole station QSPA

我们注意到各向异性耦合现象经常出现在大地震发生后的早期阶段，且都发生在观测台站靠近某个球形振荡 （Rayleigh驻波）的节线的情况下，参与耦合的球形简正模的振幅很小.大地震激发的球形简正模节线的空间分布与震源的地理位置及震源破裂方式有关.若台站远离球形简正模的节线，即使其周围上地幔中存在各向异性介质，也很难在其数据中观测到简正模各向异性S－T耦合信号.例如在2011－03－11 Mw9.0日本仙台大地震后，QSPA 不靠近0S20的节线，因而我们未能在 QSPA观测到0S20－0T21的各向异性耦合（参见图4b）.

上述各向异性S－T耦合的特征可作为在重力和地震观测数据中寻找方位各向异性S－T耦合的重要线索.例如2004－12－26 MW9.0苏门达腊大地震发生后，自由振荡简正模0S25的节点靠近台湾.台湾的多个宽带地震仪在震后18h的连续观测记录中显示了强烈的0S25－0T25耦合信号.图5a显示在台湾SSLB台的LHZ记录数据中，环形简正模0T25出现在垂直记录中，且其振幅明显大于球形简正模0S25的振幅.值得注意的是：根据不同简正模间产生耦合的选择条件[24]，地球自转不能导致0S25与0T25的耦合，因此0S25与0T25间的强耦合是方位各向异性耦合.这些现象表明台湾岛下的上地幔过渡区中可能存在较强的方位各向异性介质.

图5 台湾地震台SSLB的LHZ观测记录的振幅谱Fig.5 The amplitude spectra of LHZ records from the station SSLB of Taiwan

2010－02－27 MW8.8智利大地震后，台湾地区多个地震台不仅观测到了简正模基频波间的各向异性耦合0S25－0T25、0S19－0T20、0S20－0T21，也观测到了简正模谐频波间的耦合2S12－2T7（图6）.强烈的简正模基波间耦合出现在震后18～24h的垂向观测记录中，随后迅速衰减并消失.在台湾许多台站的垂向观测记录中还出现了0T21大于0S20，0T20大于0S19的现象（参见图6）.根据地球自转简正模S－T耦合选择规则，0S20－0T21以及0S19－0T20耦合也可能受到地球自转影响.但震后40h振幅谱中并未显示0S20－0T21、0S19－0T20耦合的迹象，其相邻的0S18也未有任何耦合的迹象.这些现象表明，智利大地震的自由振荡简正模耦合受地球自转的影响较弱.

图6 2010－02－27 Mw8.8智利大地震后6个台湾宽频带地震仪LHZ记录的振幅谱Fig.6 The LHZ spectra from six seismic stations of Taiwan after the 2010－02－27Mw8.8Chile earthquake

由上述观测和分析研究表明：即使在观测台站附近存在上地幔方位各向异性的情况下，也只有在台站靠近某个球形简正模节线的情况下，才有可能观测到长周期方位各向异性S－T耦合.而观测地球自转S－T耦合则不需要这种空间位置要求.但大地震后观测到显著的地球自转S－T耦合也非易事.只有震源机制为大型走滑型板块运动的大地震才能激发较强的环形简正模，这时科里奥利力才有可能将环形简正模耦合到垂向可观测的水平，并导致参与耦合的球形简正模的频率和振幅偏离理论值.由于参与耦合的简正模的频率相近，且地球自转S－T耦合对其频率影响较小，因此清晰观察到地球自转ST耦合至少需要35h的连续观测数据[23，25].而方位各向异性耦合衰减较快，并可导致参与耦合的简正模发生较大的频率偏移，因此震后15～24h是清晰观察各向异性S－T耦合的最佳时期.在垂向观测记录中，自转S－T耦合产生的环形简正模振幅明显小于其对应的球形简正模振幅，而方位各向异性ST耦合却经常导致环形简正模振幅接近、甚至大于其对应的球形简正模.其原因是靠近节线的球形简正模振幅本身较小，而各向异性介质还会将其部分垂向能量转移到水平方向.在地震波接收台站的长周期简正模观测数据中，自转S－T耦合信号和方位各向异性S－T耦合信号在其出现的空间、时间和强度上都有显著的差别.因此，即使二者的影响都存在，也能根据这些差异将其区分开.

5 结 论

根据大地震后赤道地震台和极地地震台记录到的各向异性S－T耦合现象，分析其特征，并结合数值模拟，可以得到以下结论：

（1）方位各向异性可导致比地球自转耦合更强的S－T耦合，但强烈的各向异性S－T耦合只发生在球形简正模的节点附近.

（2）各向异性耦合不影响环形自由振荡的Q值.因此各向异性耦合多发生在自由振荡早期，震后24h内是观察各向异性S－T耦合的最佳时期，随后耦合会随环形振荡的衰减而迅速减弱.

（3）强烈的各向异性S－T耦合使球形简正模明显偏离其本征频率，并可导致垂直方向的环形简正模T的振幅大于球形耦合简正模S的振幅.

以上结论可作为在地震长周期简正模观测数据中发现各向异性S－T耦合的搜寻规则.在地球自转对简正模耦合有影响的台站，仍然可以按照搜寻规则区别各向异性S－T耦合和自转S－T耦合.探测上地幔过渡区的各向异性是地球物理和动力大地测量研究的难点，其过程充满挑战.地球长周期简正模耦合可为我们提供一个新的探测手段，为地幔过渡区的地球物理研究提供重要的约束.

（References）

[1] Hess H H.Seismic anisotropy of the uppermost mantle under oceans.Nature，1964，203（4945）：629－631.

[2] 刘启元，邵学钟.天然地震PS转换波动力学特征的初步研究.地球物理学报，1985，28（3）：291－302.Liu Q Y，Shao X Z.Study on the dynamic characteristics of PS converted waves.Chinese J.Geophys.（Acta Geophysica Sinica）（in Chinese），1985，28（3）：291－302.

[3] Cassidy J F.Numerical experiments in broadband receiver function analysis.Bull.Seism.Soc.Am.，1992，82（3）：1453－1474.

[4] Savage M K.Lower crustal anisotropy or dipping boundaries？Effects on receiver functions and a case study in New Zealand.J.Geophys.Res.，1998，103（B7）：15069－15087.

[5] Ando M.ScS polarization anisotropy around the Pacific Ocean.J.Physics Earth，1984，32（3）：179－196.

[6] Vinnik L P，Kind R，Kosarev G L，et al.Azimuthal anisotropy in the lithosphere from observations of long－period S－wave.Geophys.J.Int.，1989，99（3）：549－559.

[7] Silver P G，Chan W W.Shear wave splitting and subcontinental mantle deformation.J.Geophys.Res.，1991，96（B10）：16429－16454.

[8] Savage M K.Seismic anisotropy and mantle deformation：What have we learned from shear wave splitting？Rev.Geophys.，1999，37（1）：65－106.

[9] Silver P G.Seismic anisotropy beneath the continents：Probing the depths of geology.Ann.Rev.Earth Planet.Sci.，1996，24（1）：385－432.

[10] Mitchell B J，Yu G K.Surface wave dispersion，regionalized velocity models，and anisotropy of the Pacific crust and upper mantle.Royal Astron.Soc.Geophys.J.，1980，63（2）：497－514.

[11] Park J，Yu Y.Seismic determination of elastic anisotropy and mantle flow.Science，1993，261（5125）：1159－1162.

[12] Yu Y，Park J.Hunting for azimuthal anisotropy beneath the Pacific Ocean region.J.Geophys.Res.，1994，99（B8）：15399－15422.

[13] Park J，Levin V.Seismic anisotropy：Tracing plate dynamics in the mantle.Science，2002，296（5567）：485－489.

[14] 张中杰.地震各向异性研究进展.地球物理学进展，2002，17（2）：281－293.Zhang Z J.A review of the seismic anisotropy and its applications.Progress in Geophysics（in Chinese），2002，17（2）：281－293.

[15] Davies G F.Dynamic Earth：Plates，Plumes and Mantle Convection.Cambridge：Cambridge Univ.Press，1999.

[16] Montagner J P，Kennett B L N.How to reconcile body－wave and normal－mode reference Earth models？Geophys.J.Int.，1996，125（1）：229－248.

[17] Vinnik L，Montagner J P.Shear wave splitting in the mantle Ps phases.Geophys.Res.Lett.，1996，23（18）：2449－2452.

[18] Vinnik L，Chevrot S，Montagner J P.Seismic evidence of flow at the base of the upper mantle.Geophys.Res.Lett.，1998，25（11）：1995－1998.

[19] Fouch M J，Fischer K M. Mantle anisotropy beneath northwest Pacific subduction zones.J.Geophys.Res.，1996，101（B7）：15987－16002.

[20] Wookey J，Kendall J M，Barruol G.Mid－mantle deformation inferred from seismic anisotropy.Nature，2002，415（6873）：777－780.

[21] Trampert J，van Heijst H J.Global azimuthal anisotropy in the transition zone.Science，2002，296（5571）：1297－1299.

[22] Park J.Free oscillations in an anisotropic earth：Path－integral asymptotics.Geophys.J.Int.，1997，129（2）：399－411.

[23] Masters G，Park J，Gilbert F.Observations of coupled spheroidal and toroidal modes.J.Geophys.Res.，1983，88（B12）：10285－10298.

[24] Dahlen F A，Tromp J.Theoretical Global Seismology.Princeton：Princeton University Press，1998：234－235.

[25] Zürn W，Laske G，Widmer－Schnidrig R，et al.Observation of Coriolis coupled modes below 1mHz.Geophys.J.Int.，2000，143（1）：113－118.

[26] Park J.The sensitivity of seismic free oscillations to upper mantle anisotropy I.Zonal symmetry.J.Geophys.Res.，1993，98（B11）：19933－19949.

[27] Oda H，Ohnishi S.The effect of regional variation of lattice preferred orientation on surface waveforms.Geophys.J.Int.，2001，144（2）：247－258.

[28] Oda H.An attempt to estimate isotropic and anisotropic lateral structure of the Earth by spectral inversion incorporating mixed coupling.Geophys.J.Int.，2005，160（2）：667－682.

[29] Backus G E.Possible forms of seismic anisotropy of the uppermost mantle under oceans.J.Geophys.Res.，1965，70（14）：3429－3439.

[30] Dziewonski A M，Anderson D L.Preliminary reference Earth model.Phys.Earth Planet.Inter.，1981，25（4）：297－356.

[31] Hu X G，Liu L T，Kroner C，et al.Observation of the seismic anisotropy effects on free oscillations below 4mHz.J.Geophys.Res.，2009，114：B07301，doi：10.1029/2008JB 005713.

Study of azimuthal anisotropy in the transition zone of the Earth′s upper mantle with the coupling of normal modes

HU Xiao－Gang，XUE Xiu－Xiu，HAO Xiao－Guang＊
Laboratory of Geodesy and Earth′s Dynamics，Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan430077，China

The azimuthal anisotropy in the upper mantle can be determined by studying body wave data or surface wave data，but it is hard to use these studies to find out evidence for azimuthal anisotropy in the transition zone.Some long period normal modes of the earth free oscillations penetrate into the transition zone.According to our estimation of coupling sensitivity kernels using a model of mantle anisotropy，the coupling between fundamental spheroidal and toroidal modes in 250～400s，such as0S20－0T21and0S25－0T25，shows peak sensitivity to azimuthal anisotropy at 400～600km depth.Different from normal mode coupling caused by Earth rotation，the anisotropic coupling modes can be clearly identified only at stations near nodes of spherical harmonics，and most of them have high resolution on 18～24－hour vertical component spectra.Anisotropic coupling is so strong that sometimes the amplitude of coupled toroidal modeis even larger than that of coupled spheroidal mode on vertical component.These characteristics provide us important clues to distinguish anisotropic coupling from rotational coupling in seismic observations.Anisotropic coupling of long－period normal modes is an important signal that determines azimuthal anisotropy structures in the transition zone of the upper mantle.

Free oscillations，Normal mode coupling，Transition zone of upper mantle，Azimuthal anisotropy

10.6038/j.issn.0001－5733.2012.06.011

P312

2011－04－19，2011－07－21收修定稿

国家自然科学基金（41174022，41021003，40874036）资助.

胡小刚，男，1963年生，副研究员，主要研究方向为地学信号处理与分析.E－mail：hxg432＠whigg.ac.cn

＊通讯作者 郝晓光，E－mail：hxg＠whigg.ac.cn

胡小刚，薛秀秀，郝晓光.利用地球简正模耦合研究上地幔过渡区方位各向异性.地球物理学报，2012，55（6）：1903－1911，

10.6038/j.issn.0001－5733.2012.06.011.

Hu X G，Xue X X，Hao X G.Study of azimuthal anisotropy in the transition zone of the Earth′s upper mantle with the coupling of normal modes.Chinese J.Geophys.（in Chinese），2012，55（6）：1903－1911，doi：10.6038/j.issn.0001－5733.2012.06.011.

（本文编辑 何 燕）