孤山川流域降水变化特征及趋势分析

李春娟，杨建虎

(1.陕西省扶风县自来水公司，陕西 扶风722200;2.陕西省眉县水利局，陕西 眉县722300)

水资源是限制西北地区生态环境和社会经济协调发展的主要因子［1］。大气降水是水资源补给的主要来源，水资源年总量与气候降水有较强的正相关关系［2］，降水变化是水资源时空分布不均的主要因素之一，也是水资源评价研究的重要组成部分。为了缓解水资源危机，认识和把握流域水循环特征规律，在此基础上进行开发利用才可能实现水资源的可持续利用的目的。本文以孤山川流域为例，统计并分析流域及周边3个雨量站点51 a的月平均降雨数据，采用Mann-Kendall检验法、五点滑动平均法、R/S分析法，研究孤山川流域降水变化特征及趋势。

1 研究区概况

孤山川流域位于陕北黄土高原与鄂尔多斯高原接壤地带，区域地貌属于毛乌素沙漠南缘与黄土丘陵沟壑的过渡地带。是黄河中游北干流主要多沙、粗沙支流之一。孤山川全长79.4 km，流域面积1 276.52 km2。孤山川流域属中温带半干旱大陆性气候，冷暖干湿四季分明，冬夏长，春秋短，雨热同期，太阳辐射强，日照时间长，气温变化强烈，年较差与日较差大，降水年际变化大，旱涝霜雹灾害多。气温时空分布由东南向西北递减，年均气温8.5℃，一月最低平均气温-8.4℃，七月份最高平均气温 24.0℃，年温差 32.4℃，历年极端最高气温38.9℃，极端最低气温 -24℃。年平均降雨量435.5 mm，年最大降雨量 849.6 mm，年最小降雨量 227.7 mm，年蒸发量1 192.2 mm，约相当降雨量的2.5倍。流域河流纵横、沟壑密布，大多属季节性河流，雨季暴涨，旱季断流，且河水含沙量高。

2 研究方法

2.1 Mann-Kendall检验法

Mann-Kendall检验法［4］主要是通过计算统计量 τ，方差和标准化变量M，来判断序列趋势是否显著。计算公式如下

式中:s为序列所有对偶观测值(Xi，Yj，i＜ j中 Xi＜ Yj)出现的次数;N为序列长度，取α=5%的显著水平，如果一时间序列有明显的趋势，则|M|＞Mα/2=1.96，M 值为正，表明具有上升或增加趋势，M值为负，则意味着下降或减少的趋势。

2.2 五点滑动平均法

滑动平均法［5］，其计算公式为…+yt+yt+1)，式中yt为t点得滑动平均值，yt=(yt-2+yt-1+yt+yt+1+yt+2)/5，五点滑动平均法分析序列变化趋势，进而拟合线性方程。

2.3 分析方法

分析方法的基本原理为［6］:对于时间序列{x(t)}t=1，2，…n，对于任意正整数定义均值序列:

累积离差:

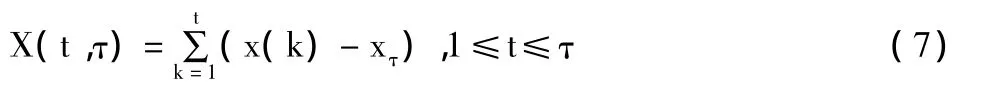
极差序列:

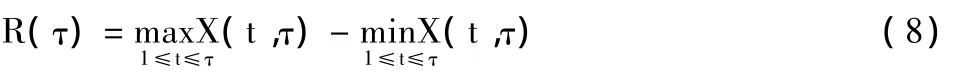
标准差序列:

对于比值如果存在如下关系:

则说明时间序列{x(t)}t=1，2，…，n存在 Hurst现象，H称为Hurst指数，H值可根据计算出的(τ，R/S)的值，在双对数坐标系(ln(τ)，ln(R/S))中用最小二乘法拟合，H对应于拟合直线的斜率。

根据H的大小可以判断时间序列趋势成分是表现为持续性(persistence)，还是反持续性(anti-persistence)。Hurst等人证明，如果{x(t)}是相互独立、方差有限的随机序列，则有H=0.5。对于不同的Hurst指数H(0＜H＜1)，存在三种情况:

(1)H=0.5时表明时间序列变化是随机的;

(2)0＜H＜0.5时表明时间序列具有长期相关性，但将来的总体趋势与过去的相反，过程具有反持续性。值越接近于0，反持续性越强;

(3)0.5＜H＜1时表明时间序列过程具有持续性，H越接近1，持续性越强。

3 降水变化特征

3.1 降水年内分配

本文选孤山川流域三个雨量站1956～2006年各月降水资料，计算出多年平均降水量年内分配(见表1)。

表1 多年平均降水量年内分配表

从表1可以看出:

1)孤山川流域降水量年内分配极不均匀，年降水大多集中在7、8、9三个月份，其中8月份所占比例最大，可占到全年降水量的26.9%，7月份所占比例次之，为25.5%，而1、2、12三个月份平均月降水量比较小，所占全年降水量的比例均在1%以下。

2)在季节分配上，夏季降水量最多，可占到全年降水量的63.9%，而冬季降水量较少，仅占全年降水量的1.9%，春秋二季各季降水量占全年降水量的10%～20%左右。

3)孤山川流域汛期主要包括每年6—9月份，历年汛期降水量大约占全年降水量的70%～90%，从占年降水量的程度来看，最高为1959年，汛期降水量为695.4 mm，占全年降水量的87.8%，最低为2003年，汛期降水量为125.9 mm，占全年降水量的61.2%。汛期降水通常集中在7月和8月，这2个月的降水量占汛期水量的67.8%，占全年降水量的52.4%左右，因此年降水的丰枯取决于汛期降水。

3.2 降水趋势分析

本文选孤山川流域三个雨量站1956～2006年各月降水资料，用Mann-Kendall检验法检验其变化趋势，结果M值为-9.8，表明该年降水序列存在减少趋势。

从近50年的降水量滑动平均来看(图1)，孤山川年降水波动较大，其中1959年、1964年、1967年、1995年、2003年的降水量较大，而1965年和1972年的降水量较少，用五点滑动平均法拟合的线性方程为y=-1.874 7x+476.93。

根据流域1956-2006年的月降水资料，春、夏、秋、冬四季的降水量分别以3-5月、6-8月、9-11月和12月～次年2月的降水累加和来代替。从近51 a的季降水变化曲线(图2、图3、图4、图5)可以得出:

图1 1956-2006年降水变化图

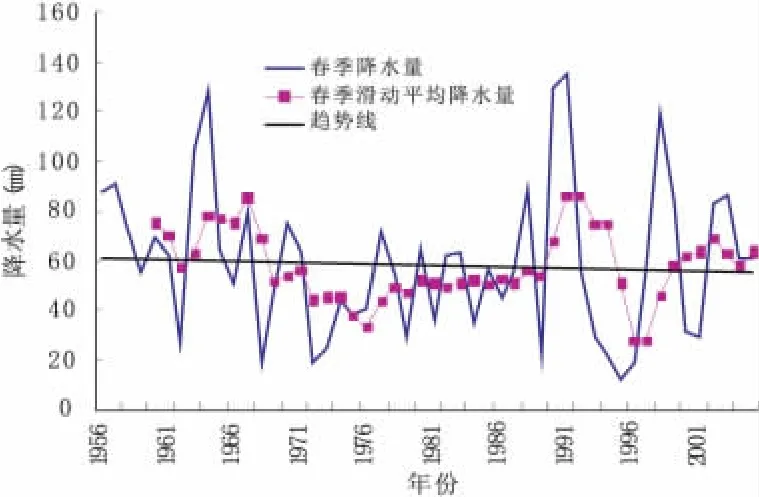
图2 1956-2006年春季降水变化图

1)春季降水减少趋势不显著，且年际间的变化较大，即呈现出突然地增加，又突然地减少，其中1964年、1990年、1991年的春季降水量较大。

2)夏季降水的减少趋势明显，夏季降水对年降水的贡献最大。从20世纪50年代后期逐渐下降，波动较小，到了60年代逐渐增加，且变化明显，70年代以后又呈现出减少的趋势。用五点滑动平均拟合的夏季降水线性方程为y=-1.344 6x+308.47，这与年降水的变化趋势较一致。

3)秋季降水的减少趋势不显著，它对年降水的贡献也较大。20世纪60年代至80年代的秋季降水量变幅较大，90年代以后有增加趋势。

4)冬季降水有增加的趋势，但趋势不显著，1971年、1978年和1989年的冬季降水较大，而1967年的冬季降水量最少。

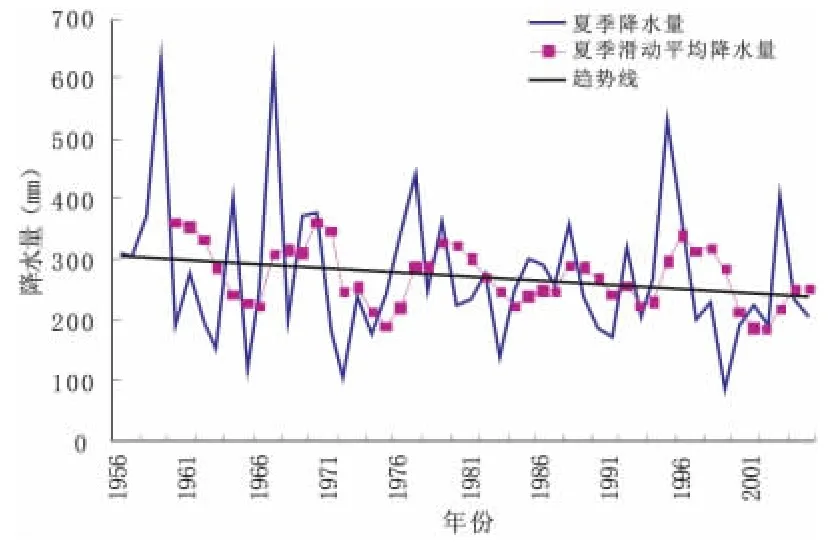
图3 1956-2006年夏季降水变化图

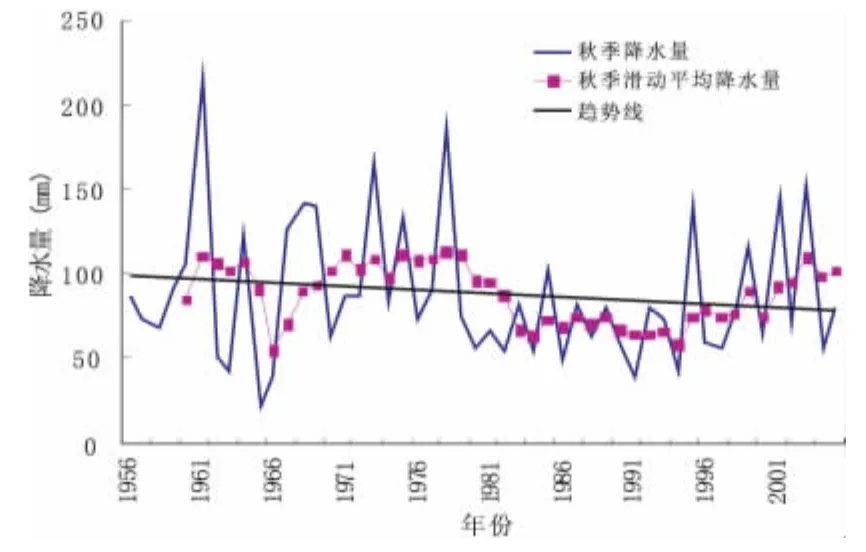
图4 1956-2006年秋季降水变化图

3.3 降水频率分析

根据1956—2005年降水资料，对参数进行分析，用皮尔逊Ⅲ型最佳适线法确定。运用频率曲线软件进行选型配线，可以得出:孤山川多年平均降水量变差系数Cv=0.31，R=Cs/Cv=2.0，从而得不同频率下年降水量分布以及汛期降水分布，结果见表2和表3。

图5 1956-2006年冬季降水变化图

3.4 降水持续性分析

趋势是指时间序列中稳定和有规则的变动。对孤山川流域降水的变化趋势，应用Mann-Kendall秩次相关法进行分析，得出在一定显著性水平下，孤山川流域降水在多年变化中呈明显下降趋势。从图6可得，通过R/S分析，得出皇甫川流域径流的Hurst指数H为0.52，大于0.5，表明降水具有持续性。孤山川流域径流表现出来的持续性说明未来流域降水量的减少具有持续性。

图6 孤山川实测年降水序列分析图

表2 不同频率年降水量

表3 汛期(6-9月)不同频率降水量

4 结论

通过对孤山川流域逐月实测降水资料进行分析，结论如下:

1)孤山川流域多年平均降水量429 mm，孤山川年降水波动较大，其中1959年、1964年、1967年、1995年、2003年的降水量较大，而1965年和1972年的降水量较少。

2)孤山川流域降水年内分配极不均，大多集中在7、8、9三个月份，其中8月份所占比例最大，可占到全年降水量的26.9%。历年汛期降水量大约占全年降水量的70%～90%，年降水的丰枯取决于汛期降水。

3)孤山川流域降水季节变化趋势不同。夏季降水的减少趋势明显，冬季相反有增加趋势，但趋势不显著，春、秋二季降水减少趋势不显著

4)利用Mann-Kendall检验法检验其变化趋势，结果M值为-9.8，表明孤山川流域降水序列存在减少趋势;利用分析法，得出孤山川流域Hurt指数H均大于0.5，表明流域降水具有持续性，结果表明孤山川流域降水减少趋势有持续性。

［1］程国栋.承载力概念的演变及西北水资源承载力的应用框架［J］.冰川冻土.2002，8(4):361～367.

［2］黄嘉佑，张镡.黄河流域旱涝与水资源分析［J］.大气科学.1996，20(6):673～678.

［3］陈操操，谢高地，甄霖.泾河流域降雨量变化特征分析［J］.资源科学.2007，29(2):172-177.

［4］刘昌明，郑红星.黄河流域水循环要素变化趋势分析［J］.自然资源学报.2003，18(2):129-135.

［5］丁晶，刘权授.随机水文学［M］.北京:中国水利水电出版社.1997.

［6］张利平，王德智，夏军，等.分析在洪水变化趋势预测中的应用研究［J］.中国农村水利水电.2005，(2):38～40.

［7］张秀丽，孙燕，祁文.北京逐日气温和降水量的长程变化特征［J］.气象科学.28(4):421-425.

［8］任国玉，吴虹，陈正洪.我国降水变化趋势的空间分析［J］.应用气象学报.2000，8(3):322～330.

［9］陈峪，高歌，任国玉，等.中国十大流域近40多年降雨量时空变化特征［J］.自然资源学报.2005，5(9):637～643.

［10］徐宗学，张玲，阮本清.北京地区降雨量时空分布规律分析［J］.干旱区地理.2006，4(2):186～192.

［11］张素琴，任振球，李松勤.全球温度变化对我国降水的影响［J］.应用气象学报.1994，8(3):333～339.

［12］张存杰，高学杰，赵红岩.全球气候变暖对西北地区秋季降雨的影响［J］.冰川冻土.2003，4(2):157～164.