金属约束下定常非理想爆轰的理论研究＊

于 明，孙宇涛，张文宏

（北京应用物理与计算数学研究所，北京100094）

高能炸药非理想爆轰问题，是爆轰物理学领域非常重要的研究内容，关系到对炸药直径效应、熄爆速度、约束效应以及驱动效率等爆轰规律的认识，特别是钝感炸药（insensitive high explosive，IHE）的非理想爆轰更受关注。与敏感炸药爆轰相比，钝感炸药爆轰具有2个特点：（1）爆速更低；（2）化学反应区更宽，因此钝感炸药的非理想爆轰现象更显著。

对炸药非理想爆轰问题的理论研究开展很早，主要理论有2类［1］：一类是流管方法，另一类是弯曲阵面法。流管方法以F.Wecken等［2］的工作为主，假定前导波阵面是平面，波后产物流线围成的流管截面是逐渐扩大的，发散流动被认为是一维的。弯曲阵面法以J.B.Bdzil等［3］的工作为主，假定前导波阵面形状为已知曲面（如一定半径的球面等），波后流动是二维的。需指出的是，J.B.Bdzil等［3］的工作是W.W.Wood等［4］的轴线一维理论成果的推广，初步揭示了二维反应区结构的特征，但在计算声速面时面临较大困难。近年来，出现更多的理论方法试图给出较精确的反应区结构特征，如W.B.Brown等［5］的最大熵增理论和S.D.Watt等［6］的流线理论等。最大熵增理论指出，对定常、自持爆轰，在流线上前导冲击波与声速线之间的熵增最大，由此可由变分方法确定前导波阵面后声速线的位置。流线理论假定波后流线是发散的直线，给定爆轰速度的径向变化关系后沿所有流线求解可以给出波阵面形状与声速线位置。以上这些理论方法仅考察了无约束或弱约束条件下的非理想爆轰流动，这些条件下声速线与前导波阵面在炸药边缘处交于一点，而金属约束（强约束）条件下声速线与前导波阵面并不相交，并且这些理论方法只给出声速线的位置，而未给出化学反应结束线的位置，而且，这些理论方法对未反应炸药和爆轰产物均采用较简单的多方指数状态方程。

本文中对钢和铝约束条件下钝感炸药PBX9502的定常非理想爆轰状态进行理论研究。理论分析可知，在惰性金属施加的强约束条件下，爆轰流场中声速线与前导冲击波阵面的相对位置同金属压缩性相关，这一点与无约束或弱约束条件下的非理想爆轰流动显著不同。当金属对炸药约束作用时，爆轰前导冲击波折射进入金属，爆轰冲击边缘角由未反应炸药的冲击波极曲线和金属的冲击波极曲线的匹配关系确定。为了更准确地分析，对未反应炸药和爆轰产物均采用JWL形式状态方程，对金属采用p（r，T）形式的状态方程［7］，炸药化学反应模型中采用三项式Lee－Tarver反应率［8］。采用过爆轰前导冲击波的流线偏转角在影响域内沿高度线性变化的假设，则由斜冲击波极曲线关系式可以求出前导冲击波阵面的形状。采用前导冲击波阵面之后的流场中的流线是直线的假设，则爆轰流动控制方程由偏微分方程变为沿流线的常微分方程，沿着所有流线求解便给出声速线与化学反应结束线的位置。理论分析同时给出约束金属折射冲击波后面的流体的流动状态。

1 爆轰前导冲击波阵面形状的求解

金属约束条件下高能炸药的定常非理想爆轰流动状态如图1所示。如果把参考坐标放在爆轰前导冲击波阵面OA与金属界面的交点O点上，则该交点附近的流动被定常化。金属与炸药爆轰波相互作用时，爆轰受边界侧向膨胀的影响呈非理想状态，因此炸药－金属界面附近的前导冲击波阵面变弯曲，如果炸药厚度Y足够大，变弯曲的前导冲击波高度被认为是L（图中OE段），则大于L处的前导冲击波阵面仍是平面，前导冲击波后的声速线为BC，化学反应结束线为BD。这时前导冲击波前的流动被认为是速度大小为DCJ的均匀来流。爆轰波与金属相互作用时，首先是前导冲击波在金属中发生折射，因此将爆轰波极曲线建立于前导冲击波上。前导冲击波的冲击状态由未反应炸药物性决定，因此给定未反应炸药状态方程和波前来流速度，可以由前导冲击波的极曲线关系得到过前导冲击波的流动偏转角θ。在边界处，由于前导冲击波后面的流动是亚声速的，因此前导冲击波在炸药－金属界面上不会产生任何反射波，这时爆轰冲击边缘角θe（前导冲击波阵面与金属界面在他们交点处的夹角）由未反应炸药前导冲击波极曲线与金属折射冲击波极曲线决定，并且这2条冲击波极曲线有共同的初始点（初始压力和初始流线转折角均为0）。

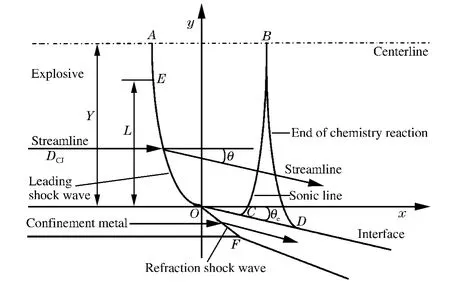
图1 金属约束条件下高能炸药的定常非理想爆轰流动状态Fig.1 Steady non－ideal flow of detonation in high explosives confined by metal

为了求出爆轰前导冲击波阵面的几何形状，假定前导冲击波阵面由函数xf＝xf（yf）来描述，并用α表示波阵面与波前速度之间的夹角，则有冲击波阵面函数斜率关系式

考虑到金属约束时爆轰冲击边缘角较小，这里采用过前导冲击波的流线偏转角在边界影响域内沿高度线性变化的假设，即在冲击波阵面OE段上有如下关系式

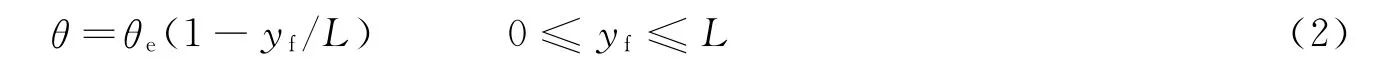
对未反应炸药，采用JWL形式的状态方程，其斜冲击波极曲线关系式为

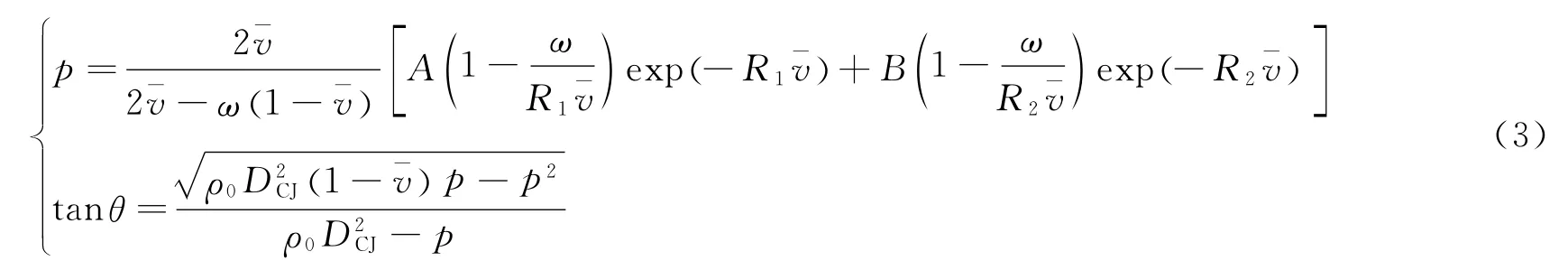
对金属，采用p（r，T）形式的状态方程，有如下表达式

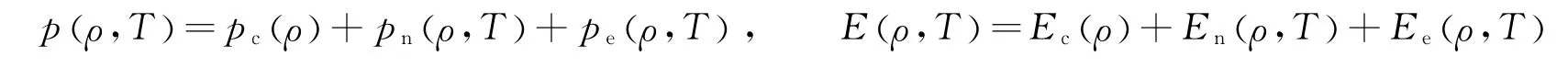
上述3项分别表示冷压（冷能）、原子核热压（原子核热能）和电子热压（电子热能），每项具体表达式见文献［7］，由此有其折射冲击波极曲线关系式

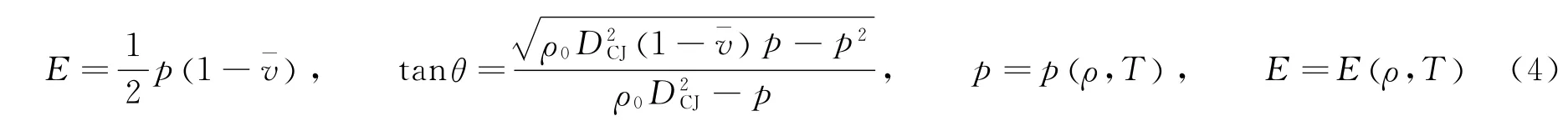
式（2）中的爆轰冲击边缘角θe由未反应炸药前导冲击波极曲线（3）和金属折射冲击波极曲线（4）的交点决定。图2中给出了钢和铝约束PBX9502炸药时未反应炸药与金属的冲击波极曲线匹配关系，实线为未反应炸药极曲线，虚线为金属极曲线，点“Cm”为金属声速点状态。由图中极曲线交点可知，钢约束时θe＝4.20°，铝约束时θe＝2.28°。

从上述思路可见，确定爆轰冲击边缘角以后，前导冲击波后任意位置处的流动偏转角θ由式（2）给出，并由式（3）迭代求出前导冲击波后的压力p和相对体积v－，进而可求出波阵面与波前速度之间的夹角α，最终由式（1）获得爆轰前导冲击波阵面的几何形状。

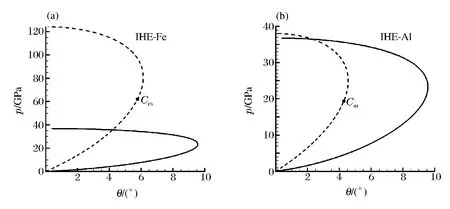
图2 未反应炸药与金属的冲击波极曲线Fig.2 Shock polar match of unreacted explosive and metals

2 爆轰化学反应区声速线和化学反应结束线的求解

爆轰化学反应区流场可由如下计化学反应的二维可压缩定常无粘流动方程来描述

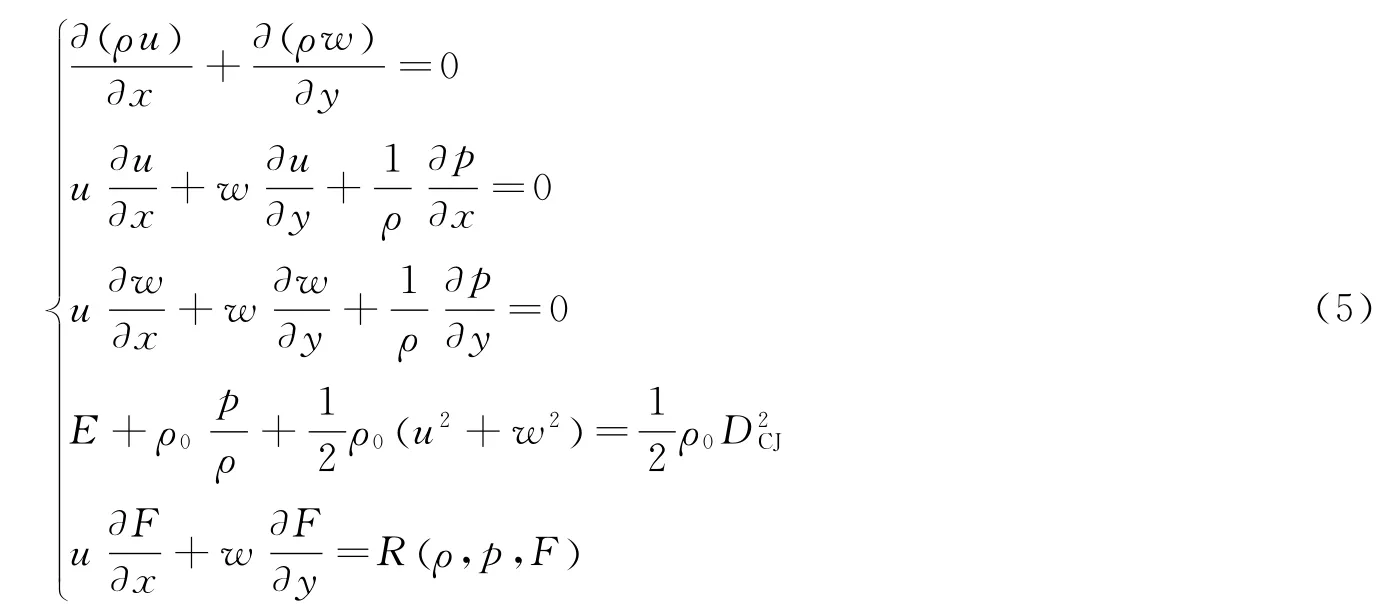
式中：F为爆轰产物的质量分数，Rρ，（p，F）为三项式Lee－Tarver反应率［8］。

为方便求解，将方程组（5）写成如下矢量－矩阵形式

式中：q＝［ρ，u，w，F］T，s（q）＝［0，0，0，R／u］T，且有通量矩阵H（q）如下

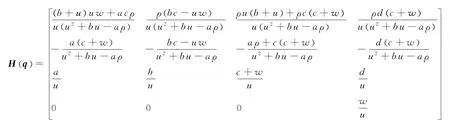
从偏微分数学理论可知，式（6）的通量矩阵有4个特征值：2个为实数，2个为复数，故它为双曲－椭圆型方程。对于实数特征值，当dy／dx＝w／u时，在特征线上成立

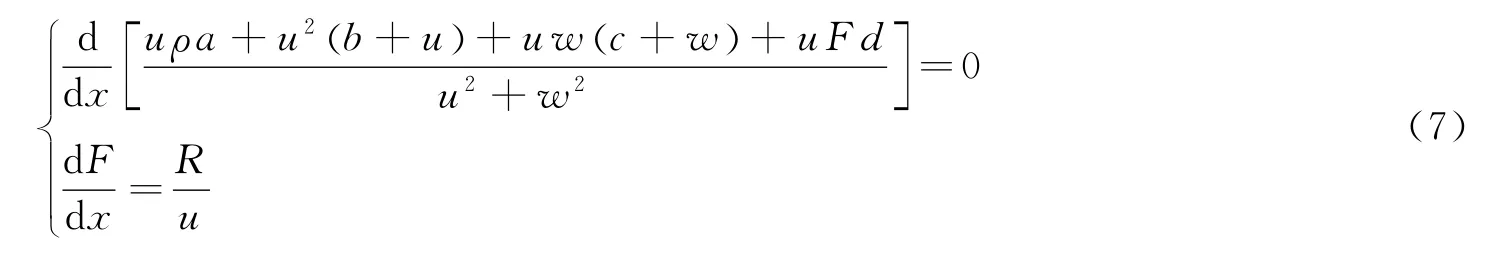
这样，偏微分方程（5）变成为沿特征线方向的常微分方程式（7）。

这里采用爆轰前导冲击波阵面之后的流场中的流线是直线的假设，则对前导冲击波阵面上的任一点以及此点处的流线偏转角θ，有过该点的流线方程为

由定常流体力学理论知，定常流动的流线就是特征线，故可得

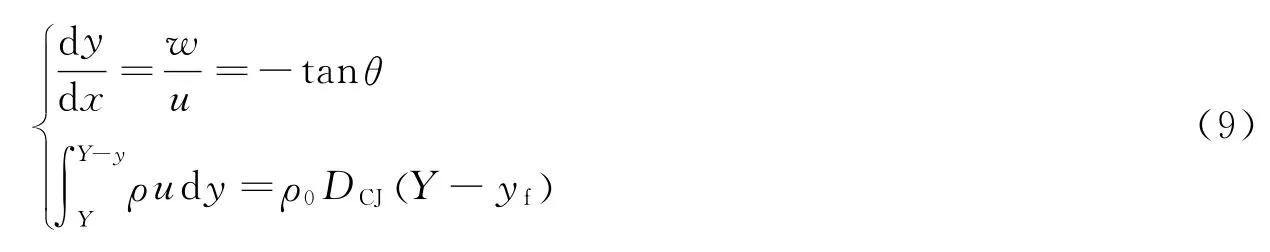
联立式（7）和（9），即沿流线方向求解，可获得任意x位置处的流动状态。

特别地，在u2＋w2＝c2F处，且cF为保持爆轰产物质量分数不变时的冻结声速，此处即为声速线的位置。在F＝1处，此处即为化学反应结束线的位置。

Lee－Tarver反应模型要求对化学反应区采用温度和压力平衡以及体积和能量可加的混合原则。在此原则下冻结声速的计算式推导如下。由化学反应区混合原则有

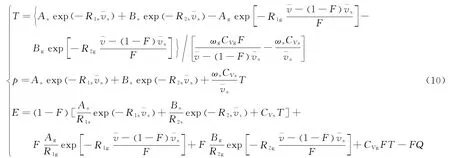
式中：下标s表示未反应炸药，g表示气体产物，T为温度，Q为单位质量炸药化学反应释放的能量。

则冻结声速可以写成如下表达式

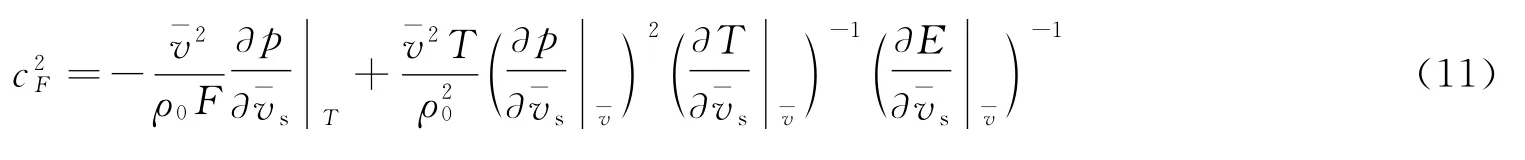
式（10）和（11）联立起来经过迭代可以消去中间变量vs从而得到cF。

3 金属折射冲击波后的流动状态

金属采用p（r，T）形式的状态方程时折射冲击波后等熵声速表达式为

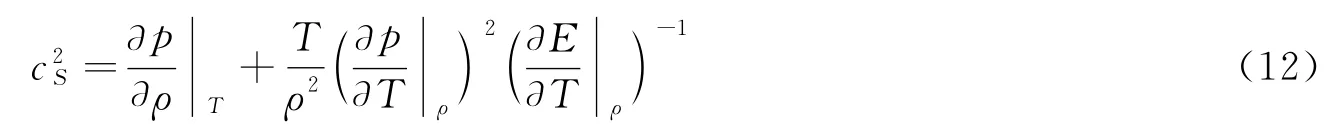
由式（4）和式（12）联立起来可以确定折射冲击波后流动是超声速还是亚声速。

4 钢和铝约束条件下钝感高能炸药的结果分析

PBX9502炸药的化学反应率参数见文献［8］，在金属约束条件下定常传播的爆轰波受边界影响的前导冲击波高度L可由文献［1］中相关公式估计。理论分析同高精度的二维Lagrange流体力学方法的数值模拟进行了比较。数值模拟时，炸药厚度为2.0cm，金属厚度为0.5cm，长度均为6.0cm；离散网格划分为250cm－1，总网格数约为1 000 000。

图3中给出了获得的钢和铝约束下物质界面附近的爆轰前导冲击波阵面形状以及声速线和化学反应结束线的位置，其中实线为理论计算结果，虚线为数值模拟结果。从比较结果可以看出，在2种金属约束条件下理论结果同数值结果符合得较好。爆轰前导冲击波阵面形状符合得好，说明采用的流线偏转角是线性变化的假设是合理的。声速线和化学反应结束线符合得好，说明采用前导冲击波阵面之后的流场中的流线是直线的假设是合理的。

从图中结果也可以看出，在金属界面附近，在流动达到声速以后经过一定距离化学反应才结束，这正是非理想爆轰的特点。在金属约束条件下，爆轰化学反应区流场中声速线与前导冲击波阵面不相交，这一点与无约束或弱约束条件下的非理想爆轰流动显著不同。

从图中结果还可以看出，由于钢的声阻抗（3.658g／（cm2·ms））较大而难于压缩，因此钢折射冲击波后面的流动是超声速；相反地，铝的声阻抗（1.495g／（cm2·ms））较小而易于压缩，因此铝折射冲击波后面的流动是亚声速。这与图2中极曲线理论结果一致，图2（a）中2曲线交点位于金属声速点下方，故流动为超声速；图2（b）中2曲线交点位于金属声速点上方，故流动为亚声速。可见约束金属可压缩性的不同导致折射冲击波后流动状态不同。

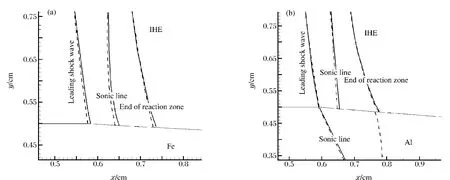
图3 金属约束条件下非理想爆轰流动特征状态Fig.3 Characteristic flow states of non－ideal detonation under metal confinement

5 结 论

本文中提出了一种研究高能炸药定常非理想爆轰的理论方法。该方法采用了过爆轰前导冲击波的流线偏转角在影响域内沿高度线性变化以及前导冲击波阵面之后的流线是直线这2点假设，并对未反应炸药和爆轰产物采用JWL形式状态方程，对金属采用p（ρ，T）形式的状态方程。本理论方法可以解析地求出炸药前导冲击波阵面的形状，以及给出前导冲击波后声速线与化学反应结束线的位置，同时给出约束金属内的流动状态：当金属声阻抗较大时，金属折射冲击波后面的流动通常为超声速，反之则为亚声速。从本理论方法获得的爆轰化学反应区结构特征和约束金属内的流动特征这些典型结果看，与高精度Lagrange流体力学数值方法的模拟结果符合良好，说明本文的理论方法具有良好的合理性和适用性。同时，本理论方法的花费远小于高精度Lagrange流体力学数值方法，说明本文的理论方法具有良好的高效性。

［1］孙承纬，卫玉章，周之奎.应用爆轰物理［M］.北京：国防工业出版社，2000.

［2］Wecken F.Non－ideal detonation with constant lateral expansion［C］∥Proceedings of the 4th International Symposium on Detonation.Silver Spring，Maryland，1965：107－116.

［3］Bdzil J B，Stewart D S.Modeling two－dimensional detonations with detonation shock dynamics［J］.Physics of Fluids A：Fluid Dynamics，1989，1（7）：1261－1267.

［4］Wood W W，Kirkwood J G.Diameter effect in condensed explosives：The relation between velocity and radius of curvature of the detonation wave［J］.Journal of Chemical Physics，1954，22（11）：1920－1924.

［5］Brown W B.Thermodynamics theory of non－ideal detonation and failure［C］∥Proceedings of the 12th International Symposium on Detonation.San Diego，California，2002：718－723.

［6］Watt S D，Sharpe G J.A streamline approach to steady non－ideal detonation theory［C］∥Proceedings of the 14th International Symposium on Detonation.Coeur d′Alene，Idaho，2010.

［7］经福谦.实验物态方程导引［M］.2版.北京：科学出版社，1999.

［8］Tarver C M，McGuire E M.Reactive flow modeling of the interaction of TATB detonation waves with inert materials［C］∥Proceedings of the 12th International Symposium on Detonation.San Diego，California，2002：641－649.