基于不确定性原理的误差理论研究探讨

杨久东，王 涛，肖 格

(1．中国矿业大学(北京)资源与安全工程学院，北京100083;2．河北理工大学交通与测绘学院，河北唐山063009;3．襄阳市国土资源局产权管理处，湖北襄阳441021)

一、引 言

误差产生的必然性已为实践所证明，随着科技水平的提高和人的认识能力的丰富，测量误差可以被人控制的愈来愈小，经典误差理论的局限性已经开始制约测量精度的评价。

精确数学的相容性理论——概率论判别事物的逻辑体系是{0，1}二值逻辑。对于是否存在的现象分析存在不足，模糊数学的可能性理论补充可弥补概率论这一不足。

试践检验结果说明，测量误差是必然事件，误差出现概率P=1．0，测量仪器的精密化，使得同一时刻、同一条件下的观测值的互差大大缩小，出现相对观测值均值¯x的密集分布，这就是相对观测值均值¯x的离散度σ。但是，实践证明，电子测量值的离散度(误差)相对于仪器误差(即均值¯x的正确度)b已退居次要或相同地位。这说明需要创立新的误差分布函数来表达误差分布规律，需要考虑系统误差和偶然误差的综合影响。

二、研究误差和误差理论的意义

正确的认识是不以人的意志为转移的客观规律，不能为了追求表面误差现象而掩盖观测值本身(均值)的误差。

误差与不确定度理论可以帮助正确地组织测量，合理地设计仪器，正确地选用测量仪器与选定测量方法，能以最经济的方式取得[pvv]=最小的最佳结果。

为误差向不确定度的过渡建立联系桥梁，完善误差与不确定度理论。

研究误差就是为定义出正确的模糊权奠定基础，以实现动态优化设计，真正地实现平差结果[pvv]=最小的原则。

研究误差为建立误差与不确定度评价体系奠定基础。

三、测量不确定度

1．不确定度概念

测量误差的大小代表着测量结果质量的高低，也代表着观测结果的不确定性。不确定度测量和计量科学技术密切相关，它代表着测量技术水平，测量质量的高低，以及尚未确定的状况。由此可见，提出不确定度概念的真正意义就在于评价测量结果的质量，表达对测量结果的认识程度。

不确定度虽然来源于误差，但又区别于误差，其区分点应包括但不限于以下两点：①应具有不确定性分布函数;②与误差完全不相同的表达形式，既能表达观测值的不确定性水平或可疑程度，又能表达误差的大小、离散程度、峰态系统误差和偶然误差状况等定性、定量分析结果。

基于上述实践的认识过程，本文认为，不确定度是测量误差的延伸概念，它具有误差的全部属性，出现概率p=1．0。同时不确定度又不同于误差，其重要标志就是它具有代表人类认识能力不足状况的不确定性水平值。

目前国际上把不确定度基本上分为以下两种。

(1)可测不确定度

可测不确定度指的是在精确数学范畴里可根据概率统计规律计算误差极值的不确定度。通常以偶然中误差的2～3倍(误差置信概率为95．5% ～99．7%)来估计误差的上界。由于均值有误差，所以可测不确定度尚不能完全表达真实的不确定度。

(2)不可测的不确定度

不可测的不确定度指的是那些无法按概率统计规律估计误差上界的不确定度。例如：系统误差等不受经典误差理论覆盖，所以概率论对系统误差是无效的。

2．不确定度的合理的定性、定量分析评价指标问题

不确定度是由测量误差引申而来的概念，首先具有误差的性质。因此在不确定度的定性表达指标中，必须表达出系统误差和偶然误差的分布状况。系统误差方面要表达出均值x相对真值X偏离的误差大小状况和峰态状况(左、右偏);偶然误差方面要表达出此偶然误差相对均值x的离散程度。不同的国家有不同的测量规程，不同的测量仪器具有不同的观测精度等级，不同的施测人员有不同的施测结果和误差结果。上述的3个“不同”就造成了国际、国内间不确定度的千差万别，使得不确定度的统一评价成为目前的国际难题。为解决这一国际难题，需要建立不受国家、地区、仪器、施测人员条件限制的定性、定量、定质量水平(不确定性水平)的不确定度定义。

四、不确定性分布函数的建立探讨

不确定度是误差的延伸概念，它具有误差的全部属性。而误差的分布函数是误差出现的可能性分布，因而不确定性与误差出现的可能性分布密切相关。而误差出现可能性系指对误差出现的确知程度，因而它的补集即为未知的(可疑的或缺欠的，认识不到的)不确定性分布。可能性分布Ⅱx，则它的不确定性分布

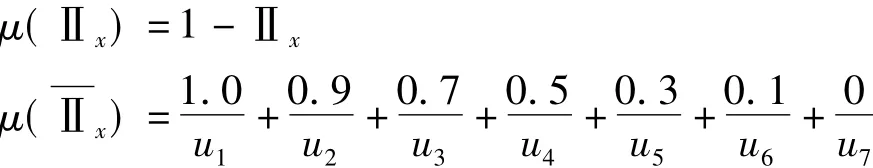
(1)误差全集u～的不确定性分布

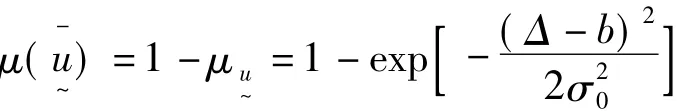
则全集u～的分布图形如图1所示。

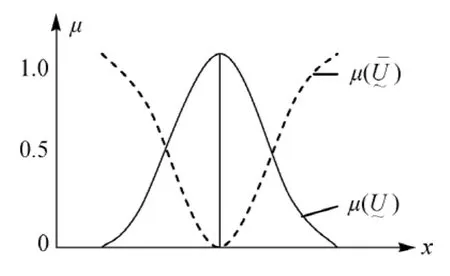
图1

(2)离散误差子集A～的不确定性分布函数

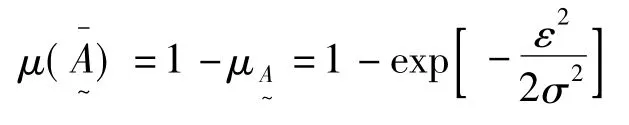
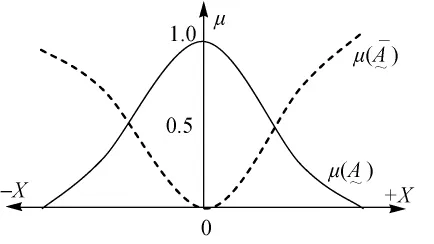
图2

离散误差子集A～的不确定性函数如表1所示。

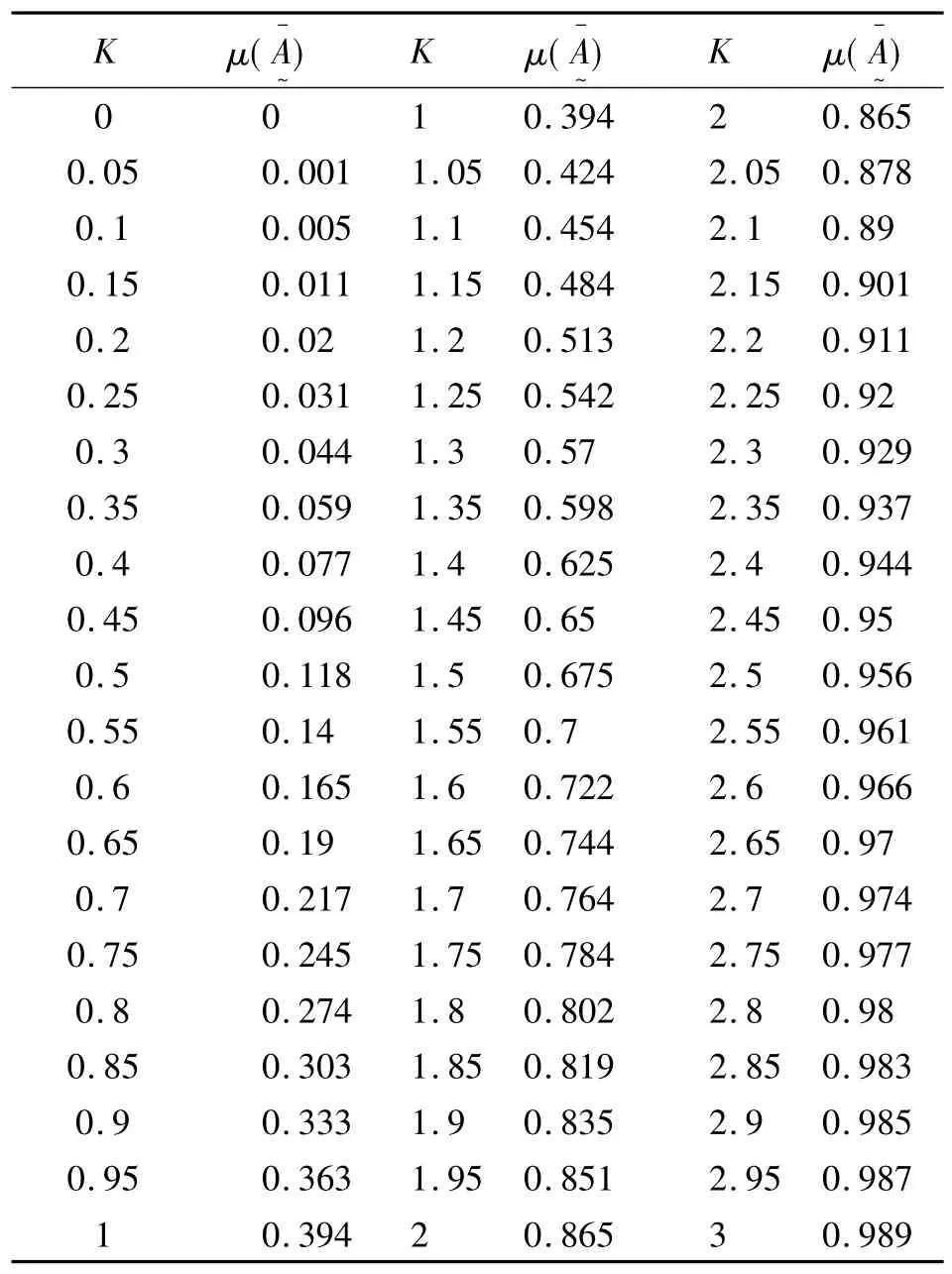
表1

由表中数据可以看出，离散误差的置信限越大，即随K值加大，不确定性也加大，K=0．5时，

(3)系统误差的不确定性分布

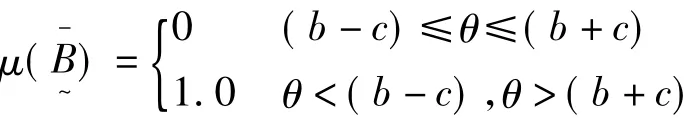
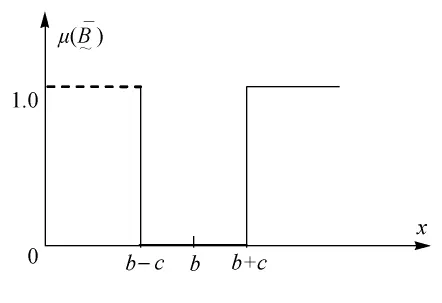
图3

(4)其它的相关不确定性分布

梯形的不确定性分布，它是由一个升半梯形和降半梯形构成的，如图4所示。

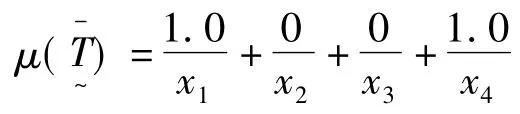
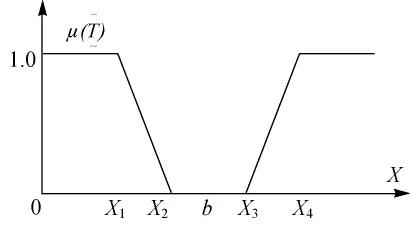
图4

三角形不确定性分布如图5所示。

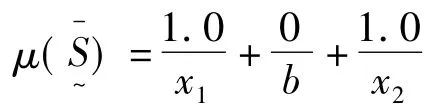
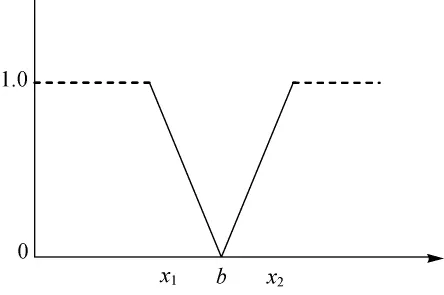
图5

五、测量不确定度的现代定义

其必备附件：分布曲线图，可以是可能性也可是不确定性分布曲线图。

六、结束语

测绘工程和计量试验的测量结果都具有误差，误差自始至终存在于一切科学试验和测量过程之中，故误差是测量的必然事件，所以误差的出现概率p=1．0。在这一先决条件下，研究建立的不确定性分布函数作为误差向不确定度过渡的桥梁已经成为现实。

试验和测量工作也是不断发展的，是无止境的。基于模糊数学和系统论的方法进行研究，进行理论创新，建立了“基于不确定性原理的现代误差理论”将对误差理论研究产生深远意义。

[1]郑党儿．简明测量不确定度评定方法与实例[M]．北京：中国计量出版社，2005．

[2]张世箕．测量误差及数据处理[M]．北京：科学出版社，1979．

[3]肖明耀．实验误差估计与数据处理[M]．北京：科学出版社，1980．

[4]刘智敏．不确定度原理[M]．北京：中国计量出版社，1963．

[5]国际标准化组织．测量不确定度表达指南[M]．肖明耀，康金玉，译．北京：中国计量出版社，1994．

[6]PARRATT L G．Porbability and Exper-imental Errors in Science[M]．NewYork：John Wiley Press，1961：168，169，178．