基于神经网络坐标差学习的GPS坐标转换

宋 雷，胡伍生

(1．东南大学交通学院，江苏南京210096;2．山东交通学院 土木工程系，山东济南250357)

一、引 言

GPS定位技术采用WGS-84空间直角坐标系，无论是静态模式或实时动态模式(RTK)，GPS测量得到的都是WGS-84坐标系下的坐标。我国的测绘生产先后采用过1954北京坐标系、1980西安坐标系和2000国家大地坐标系(CGCS2000)。此外，有较多城市为了避免高斯投影变形带来的误差，采用地方独立坐标系统。把GPS测量的WGS-84坐标转换到工程实际应用的坐标系统是工程测量中经常遇到的问题[1]。

工程应用中，常用的坐标转换方法有三维坐标转换的七参数模型法(Bursa-Wolf模型)和平面坐标转换的四参数模型法[2-3]。随着计算技术的进步，神经网络方法越来越多地应用于工程计算之中，神经网络方法在GPS高程转换等方面有较多研究，并取得了较好的结果[4]。但是从收集到的研究文献来看，利用神经网络进行坐标转换的研究还较少，现有相关文献都没有给出神经网络与传统方法计算的比较结果[5-6]。

本文提出基于神经网络坐标差学习的GPS坐标转换的新方法，该方法不需要求取统一的区域转换参数，对于较大区域或城市，通过对坐标差的学习，转换坐标也能很好地与局部区域的坐标符合。利用某区域GPS控制网的平差结果基于该方法将WGS-84坐标转换为1980西安坐标，与现有文献的结果相比，新方法提高了神经网络GPS坐标转换的精度，并与传统坐标转换方法的结果进行比较，给出精度比较的统计结果。

二、BP神经网络原理

人工神经网络属于自适应非线性动力学系统，只要隐含层有足够的神经元，几乎可以任意精度逼近任何感兴趣的函数。常用的BP神经网络包括3层结构，输入向量P的每个元素均通过权值矩阵W和每个神经元相连，每个神经元有一个偏置值bi、一个累加器、一个传输函数f和一个输出ai，每层中所有神经元的输出结合在一起，可以得到一个输出向量a，网络的输出为输出层，而其他层为隐含层。输入层和输出层结构是由实际问题本身决定的，隐含层数量和各隐含层神经元数目应根据学习集样本数量和研究问题的复杂程度进行调整。本文研究中，隐含层中使用sigmoid函数，输出层中使用pureline函数，因为sigmoid函数的标准输入、输出限定为[0，1]，故将学习集的GPS点的坐标和坐标差转化到[0．2，0．8]中，以避开网络输出的饱和区[7-8]，所以在网络中增加了输入(出)转换层，5层神经网络结构如图1所示。

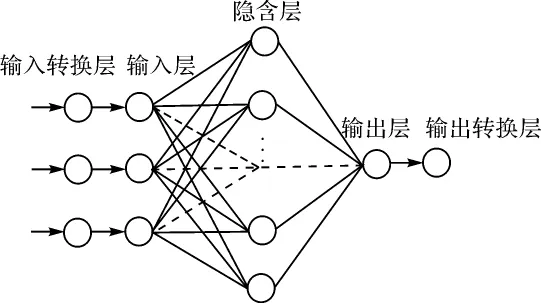
图1 5层神经网络结构

BP算法的性能指数为均方误差，多层网络的反向传播算法(BP算法)的输入是一个网络正确行为的样本集合。其中，Pq为网络的一次输入，tq为对应的目标输出，将学习集所有的网络输出与目标输出进行比较，以网络的均方误差作为性能指数，得

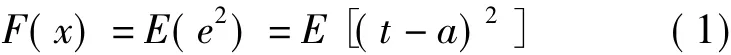
式中，t为目标输出;a为实际输出;E表示求期望值，期望在所有输入/输出对上求得。性能优化的过程就是调整网络权值和偏置值使均方误差最小。BP算法基本步骤为：

1)选定权系数初值，权系数矩阵的初始化可以随机赋值为接近于零的非零值，可使网络训练不离开性能曲面，从而避开可能的局部极小点。

2)从输入层开始，逐层计算每个节点的输入值和输出值，最后计算出网络输出值

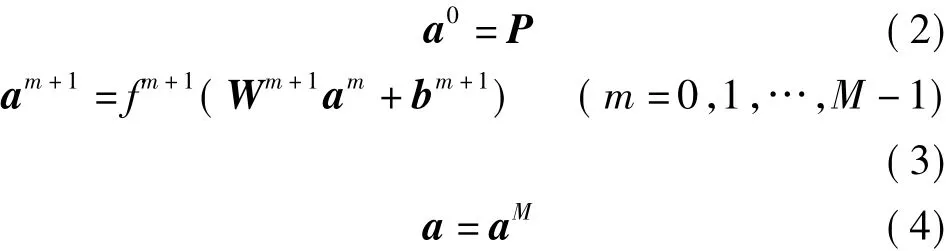
3)通过网络将敏感性反向传播

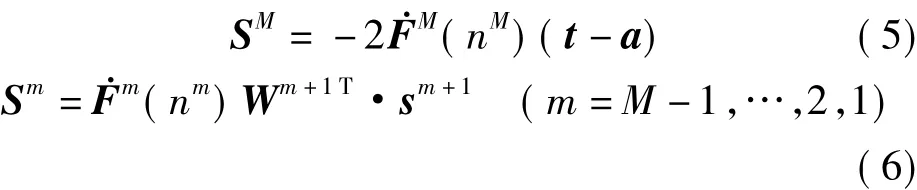
4)使用近似最速下降法更新权值和偏置值

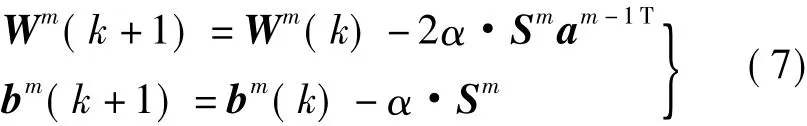
式中，P为输入向量;W为权值矩阵;f为传输函数;a为输出向量;bi为偏置值。在正向传递过程中，输入信息从输入层经隐含层逐层计算传向输出层，如果在输出层没有得到期望的输出，则计算输出层的误差变化值，通过网络将敏感性反向传播，更新各层神经元的权值和偏置值，直至均方误差最小化。

三、实例计算

1．数据资料

区域内共布设90个GPS网点，点间平均距离约为10 km。该GPS网采用Leica双频GPS接收机施测，作业方式为经典静态相对定位测量模式。卫星截止高度角为10°，采样间隔为15 s，每个点位均观测两个时段6 h以上，基线处理和平差计算采用GPSuvery软件进行，控制网在WGS-84下进行无约束平差，点位中误差的数量级为毫米级。GPS控制网中联测有4个一等国家三角点和9个二等国家三角点，这13个点同时具有1980西安坐标系坐标，可以作为坐标转换联测点和起算点使用。利用13个坐标公共点的1980西安坐标系坐标作为起算数据在GPSuvery软件进行二维约束平差，得到所有GPS网点的1980西安坐标系坐标，并作为坐标转换的比较数据。13个公共点和其他GPS网点的分布如图2所示。

图2 GPS点分布图

2．神经网络坐标差学习的坐标转换方法

1)将GPS观测WGS-84坐标系中的大地坐标通过高斯投影正算，转换为WGS-84椭球面的平面坐标，在投影过程中，中央子午线的设定应与1980西安坐标系的中央子午线相同。

2)由于13个坐标公共点上同时具有1980西安坐标系和WGS-84坐标系两套坐标，求取两套坐标的平面坐标差，两套坐标的 x坐标差区间为[-1．354 3，-0．945 65]，y 坐 标 差 范 围 为[116．999 2，117．404 5]，坐标误差主要来自于1980西安坐标系与WGS-84坐标系椭球参数和定向差异，也受到观测误差的影响。

3)将输入层元素取为WGS-84平面坐标和坐标差(x84，y84;Δx，Δy)，输出层元素取为坐标差(Δx，Δy)，利用公共点的信息组成的学习集样本为：(xi，yi;Δx，Δy)(i=1，2，…，13)。

4)利用BP神经网络仿真软件，依问题定义输入层元素为2，网络参数个数为12，输出层元素为2，利用给定学习集样本对网络进行训练，反复迭代直至学习误差小于预定值0．03m。

5)用训练好的神经网络参数按点的WGS-84平面坐标(x84，y84)求取区域内全部GPS点坐标差，坐标差与WGS-84平面坐标之和，即为转换后的1980西安坐标系坐标。这样即将WGS-84坐标转换为1980西安坐标。

隐含层所需要的神经元的数目的确定较为复杂，一般情况下，隐含层单元数过少，网络不能逼近复杂的变化，可能得不到良好的训练结果，但是隐含层单元数过多，网络响应只改善训练组匹配的精确度，缺乏泛化性。

四、结果分析

分别用3种方法进行坐标转换，首先利用13个坐标公共点的坐标差在神经网络仿真程序中对网络进行训练;其次利用训练的网络参数计算其他点的坐标差，将计算得到的坐标差加上WGS-84平面坐标即为1980西安坐标;然后利用13个坐标公共点计算区域平面坐标转换四参数，利用四参数模型计算其他点的1980西安坐标;最后利用WGS-84三维坐标和13个坐标公共点平面坐标与正常高计算区域三维坐标转换七参数，利用七参数模型计算其他点在1980西安坐标系参考椭球中的三维坐标，再通过高斯投影正算，转换为1980西安坐标系的平面坐标。

分别将3种方法转换的1980西安坐标系坐标结果与二维约束平差的结果进行比较，不同方法转换的13个点的坐标与二维约束平差值之差统计结果见表1。

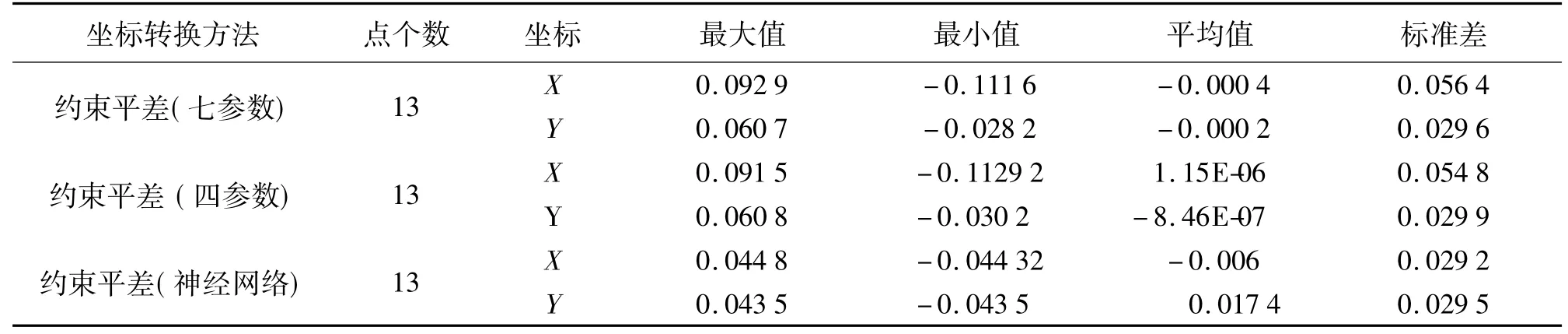
表1 公共点的转换坐标与二维约束平差值之差统计结果 m

13个坐标公共点中4个为国家一等三角点、9个为国家二等三角点，其1980西安坐标系坐标为传统三角测量方式的成果，点位精度为厘米级。由于研究区域较大，1980西安坐标系椭球参数和定向与WGS-84坐标系有差异，两套坐标差并非常数，坐标公共点的两套坐标的坐标差变化幅度达0．4 m，且没有规律性，从统计结果可以看出，神经网络方法可以较好地逼近这种无规律的差异，其坐标转换的精度优于常规方法。

对于没有参与计算参数或参加网络训练的77个点，不同转换方法的坐标与二维约束平差值之差统计结果见表2。

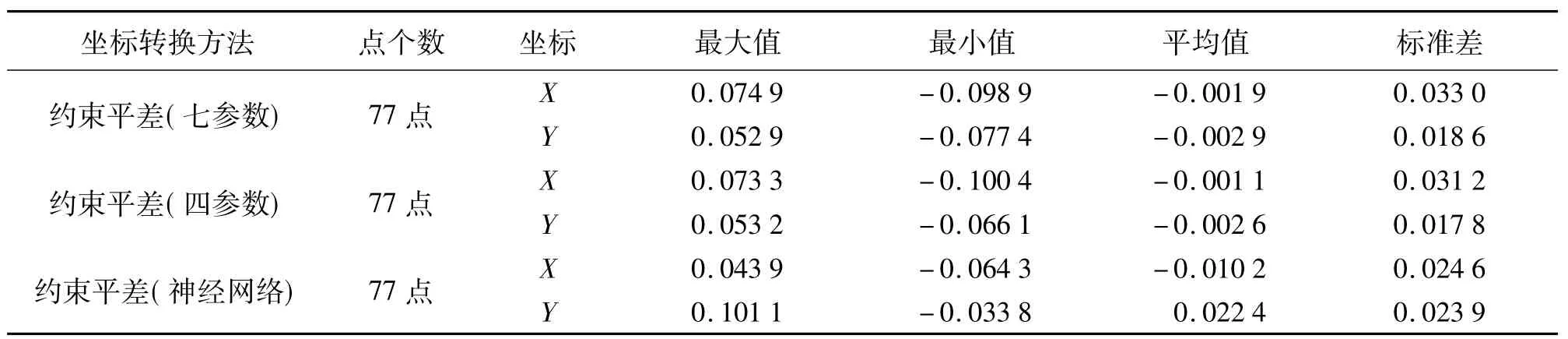
表2 GPS点的转换坐标与二维约束平差值之差统计结果 m

从表2比较结果可以看出，七参数法和四参数法转换结果差异不大，由于七参数转换模型受高程异常的影响，精度略低。利用神经网络坐标差学习方法进行坐标转换的x坐标转换的精度优于传统方法，其y坐标转换的精度略低于传统方法，x坐标和y坐标精度基本相当，接近传统三角测量成果的点位精度，综合评价为神经网络坐标差学习方法略优且精度较均匀。

五、结 论

从坐标转换结果来看，各种坐标转换方法的精度均为厘米级，误差主要是投影基准不同引起的误差和测量误差，也有转换模型带来的误差。通过本文的研究，可得以下结论。

1)神经网络方法可以模拟复杂的变化关系，利用神经网络进行坐标转换完全可行，其模拟精度可达到厘米级，利用神经网络坐标差学习方法进行坐标转换的x坐标和y坐标精度基本相当，精度较均匀。

2)根据精度统计结果比较来看，与传统的坐标转换方法相比，神经网络方法略优，但优势并不特别明显，这是因为厘米级坐标转换误差主要来自观测误差，并非转换模型所致。

3)初始权值的设置、学习集样本子样次序等都会对最终结果产生影响。这也是人工神经网络在工程应用中的缺点之一，但从计算结果比较来看，不同初始权值或样本子样次序结果差异为毫米级，可以忽略其影响。隐含层神经元个数也会影响结果，一般的，网络参数应小于学习集样本个数。

4)神经网络一般不能检测学习集样本中的粗差。在实际应用中，应选择适当的学习集样本，并在学习集样本中事先进行粗差的探测。

[1]姜卫平，马强，刘鸿飞．CORS系统中坐标移动转换方法及应用[J]．武汉大学学报：信息科学版，2008，33(8)，775-778．

[2]曾怀恩，黄声享．三维坐标转换参数求解的一种直接搜索法[J]．武汉大学学报：信息科学版，2008，33(11)：1118-1121．

[3]杨国清，张予东．平面控制网四参数法坐标转换与残差内插[J]．测绘通报，2010(11)：48-50．

[4]宋雷 ，黄腾 ，方剑 ，等．基于贝叶斯正则化BP神经网络的GPS高程转换[J]．西南交通大学学报：自然科学版，2008，43(6)：724-728．

[5]韩敏，田雪．基于神经网络的GPS坐标转换方法研究[J]．大连理工大学学报，2005，45(4)：603-606．

[6]吴兆福，高飞，宫鹏．基于BP神经网络的GPS坐标转换[J]．工程勘察，2004(4)：58-63．

[7]宋雷，方剑，周旭华，等．Bayesian正则化BP神经网络拟合两类似大地水准面[J]．武汉大学学报：信息科学版，2009，34(5)：553-555．

[8]SONG Lei，HU Xiaoqing．Fitting the GPS/Leveling Quasi-Geoid Using Bayesian-Regulation BP Neural Network[J]．Applied Mechanics and Materials，2011，90-93：2903-2906．