错误发现率的经验估计和应用*
王 婷,曾 平,黄水平,赵华硕
1)徐州医学院公共卫生学院流行病与卫生统计学教研室徐州 221002 2)南京医科大学公共卫生学院流行病与卫生统计学教研室南京 210029
#通讯作者,男,1982年7月生,硕士,助教,研究方向:高纬数据分析和贝叶斯统计,E-mail:zpstat@xzmc.edu.cn
错误发现率的经验估计和应用*
王 婷1),曾 平1,2)#,黄水平1),赵华硕1)
1)徐州医学院公共卫生学院流行病与卫生统计学教研室徐州 221002 2)南京医科大学公共卫生学院流行病与卫生统计学教研室南京 210029
#通讯作者,男,1982年7月生,硕士,助教,研究方向:高纬数据分析和贝叶斯统计,E-mail:zpstat@xzmc.edu.cn
微阵列数据;错误发现率;经验贝叶斯;密度估计
目的:研究大规模数据中的密度、无效分布和错误发现率的经验贝叶斯估计和应用。方法:对2个微阵列数据的贝叶斯模型,采用Poisson回归方法估计密度函数,并在此基础上经验估计贝叶斯错误发现率和局部错误发现率。结果:基于Poisson回归方法的密度估计为无效分布和错误发现率的经验贝叶斯估计提供了恰当的方法选择。结论:大规模数据的平行结构使得对错误发现率和无效分布的估计变得可能。
错误发现率(false discovery rate,FDR)在大规模数据分析中起着十分重要的作用[1-2],被越来越多地应用在微阵列和功能磁共振成像等领域[3-4]。FDR可以根据尾部面积和密度定义,前者以最初提出的FDR和阳性错误发现率(positives false discovery rate,pFDR)为代表[5],后者主要指局部FDR(local false discovery rate,locfdr)[6]。除了具有现实的应用价值外,FDR一个吸引人的地方在于,它同时具有频率统计的性质和可解释的贝叶斯含义[5],此外,大规模数据使得直接估计FDR变得可能,因此FDR也具有经验贝叶斯的意义。Benjamini和Hochberg[1]提供了一个十分有用的控制程序,保证FDR不大于一个预先设定的水准,与控制过程相反,该文主要研究在贝叶斯统计的框架下对FDR进行经验估计,包括估计基于尾部面积的FDR和locfdr。
1 方法与原理
1.1 理论无效分布 设m个检验的无效假设(zeroassumption,ZA)和备择假设为:H0i=0和H1i=1,统计量zi可由其他统计量转换而来,例如:

Φ、Tv分别表示正态和自由度为v的t变量累计分布函数。图1给出了2个微阵列数据z值的直方图[7-8],前者描述了50个正常对照和52个前列腺癌患者6 033个基因的表达水平,后者描述了45例急性淋巴细胞白血病患者和27例急性髓性白血病患者7 128个基因的表达水平。目的都是希望发现哪些基因在2组人群中存在表达差异。显然如果H0i=0成立,则Z~N(0,1),见图1的虚线,此后称N(0,1)为理论无效分布。图1显示前列腺癌数据中0附近的z值和N(0,1)比较吻合,但白血病数据中0附近的z值明显异于N(0,1)。但后文中仍然首先假设白血病数据的理论无效分布是满足的。
1.2 贝叶斯模型 假设所有基因只属于差别表达和无差别表达两种情况[9],设H0=0的先验概率为π0,H1=1的先验概率为1-π0,H0=0时z值的密度和分布函数分别为f0、F0,H1=1时z值的密度和分布函数分别为f1、F1。则z值具有混合边际密度f(z)=π0f0(z)+(1-π0)f1(z)和混合分布函数F(z)=π0F0(z)+(1-π0)F1(z)。如以Γ=(Z≤z)作为拒绝域,根据贝叶斯定理FDR(z)=π0F0(z)/F(z)和locfdr(z)=Pr(H0|Z=z)=π0f0(z)/f (z)[6]。FDR(z)可看作是后验尾部面积,locfdr(z)可看作是后验概率,因此从贝叶斯角度看locfdr(z)更具有可解释性。两者之间的关系为E(locfdr)= FDR。

图1 前列腺癌(上)和白血病(下)数
1.3 经验贝叶斯 按照前面的假设,如H0=0成立,则f0(z)=N(0,1),F0(z)=Φ,在微阵列数据中由于稀疏的原因,π0多大于0.90,此时即使取π0= 1也不会对FDR的估计产生很大的影响,因此FDR的完全贝叶斯分析只需要给f(z)或F(z)指定先验,但是微阵列的大规模平行结构能够直接应用数据估计f(z)或F(z),由此得到FDR的经验贝叶斯模型。累积分布函数F最直接的估计是经验分布:¯F(z)= #{Z≤z}/m。FDR的非参数经验贝叶斯估计值为:
FDR(z)=π0F0(z)/¯F(z)
例如对前列腺癌数据,如果选择Γ={Z≤-3},取π0=1,有F0(-3)=1.35×10-3,#{Z∈Γ}=49, FDR(-3)=mF0/49=0.166,这意味着在49个差别基因中大约有1/6属于错误识别。

1.5 经验无效分布 假设f0=N(0,1),从图1可见理论无效分布对前列腺癌数据是合理的,但对白血病微阵列那样的高维数据,在这种情况有必要重新选择更加合适的无效分布。在传统的单个假设检验中,应用者只能被动接受理论无效分布,但在大规模数据分析中能够利用数据估计无效分布,称之为经验无效分布[10]。如图1,虽然不能明确哪些基因来源于H0=0或是H1=1,但是几乎可以肯定的是,绝大多数存在于0附近的基因应该来自H0=0,这些基因的z值可用来估计无效分布,上述的假设称为零假设(zero assumption,ZA): f1(z)=0,z∈[-a,a]。a为一个固定的截点,比如a=0.5。仍然假设经验无效分布为正态分布,但具有不一样的参数:f0ZA=N(z|μ,σ2)。ZA暗示,如果f0ZA为正态分布,那么0附近的z值应该和f=π0f0ZA一致,根据这个原理可采用中心匹配的方法估计参数N0、μ、σ2[11]。
2 结果
见表1。选择a=0.5时的参数估计值,此时前列腺癌和白血病数据中#{z∈(-0.5,0.5)}分别为2 112和1 571。图2给出了不同z值的locfdr,此时前列腺癌和白血病数据中locfdr(z)≤0.2的基因数分别为42和202个,可见经验无效分布对白血病数据结果的影响之大,而前列腺癌数据结果的影响主要来自于π0。
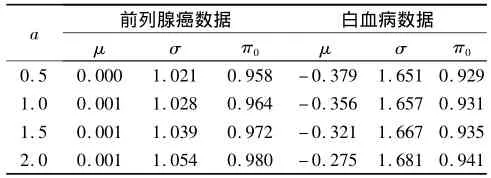
表1 不同a值对应的经验无效分布参数估计值

图2 前列腺癌(上)和白血病(下)数据的locfdr
3 讨论
FDR在大规模数据分析中具有十分现实的应用性,虽然是在频率统计下发展起来的,但同时也具有可解释的贝叶斯和经验贝叶斯含义。频率统计意义下的FDR和经典的假设检验中基于尾部面积的统计决策思维是一致的,而locfdr则具有贝叶斯后验概率的意义。Benjamini和Hochberg关于FDR的控制程序及贝叶斯FDR都是相对一个拒绝域而言的,但它们并没有对单个 z值给予任何陈述,而locfdr基于单个统计量,能够量化zi>zj时存在的FDR差别,而这种差别可能正是研究者所关心的。
但是估计locfdr要比估计基于尾部面积的FDR更加困难,前者涉及密度估计,后者只需要估计经验分布即可。Poisson回归方法为估计密度函数提供了足够高的精度和准确度,即使是在z值具有相关性时仍然能够得到满意的结果(微阵列数据常常存在相关)。除 Poisson回归方法外,其他方法如Grenander密度估计也可用来估计边际密度[12],前者的优势在于将密度估计转化为了更加熟悉的回归理论,并且能够用来进一步对FDR进行光滑估计,能在常用的软件中执行,如R软件的glm函数。但Poisson回归方法中引入了额外的参数如组段和多项式(或样条函数)的自由度,对某些异常数据可能需要更加细致地选择和调整。Efron等[6]采用了基于置换检验的logistic回归,用f0(z)/f(z)的比值间接估计locfdr。
高维数据分析中另一个十分重要的问题是,理论无效分布常常被违背,如白血病数据,在这种情况FDR的估计明显错误,但大规模平行数据结构能够对无效分布进行经验估计。作者选择ZA条件下的匹配估计方法发现,无效分布的参数依赖选择的固定常数a,但是在一定范围内a的影响有限。a越小,对ZA条件的信心越高,此时偏倚减小,但同时用于估计参数的数据量变少,因此导致方差增加,a越大导致的结果相反,也即是存在一个偏倚和方差的平衡选择;此外,ZA条件也对混合分布模型的可识别性起了重要作用。作者选择了a=0.5这个相对保险的截点,此时的数据量也足以精确估计参数,但是关于截点a的自适应选择仍是有必要的。
[1]Benjamini Y,Hochberg Y.Controlling the false discovery rate:a practical and powerful approach to multiple testing[J].J Royal Statist Soc:Series B,1995,57(1):289
[2]Benjamini Y.Discovering the false discovery rate[J].J Royal Statist Soc:Series B,2010,72(4):405
[3]Dudoit S,Shaffer JP,Boldrick JC.Multiple hypothesis testing in microarray experiments[J].Statist Sci,2003,18(1):71
[4]Lazar N.The statistical analysis of functional MRI data[M].New York:Springer,2008.
[5]Storey JD.The positive false discovery rate:a Bayesian interpretation and the q-value[J].Ann Statist,2003,31 (6):2013
[6]Efron B,Tibshirani R,Storey JD,et al.Empirical Bayes analysis of a microarray experiment[J].J Am Statist Ass,2001,96(456):1151
[7]Singh D,Febbo PG,Ross K,et al.Gene expression correlates of clinical prostate cancer behavior[J].Cancer Cell,2002,1(2):203
[8]Golub TR,Slonim DK,Tamayo P,et al.Molecular classification of cancer:class discovery and class prediction by gene expression monitoring[J].Science,1999,286(5439):531
[9]Efron B.Microarrays,empirical Bayes,and the twogroups model[J].Statistical Science,2008,23(11):1
[10]Efron B.Large-scale stimultaneous hypothesis testing:the choice of a hull hypothesis[J].J Am Statist Ass,2004,99(1):96
[11]Efron B.Doing thousands of hypothesis tests at the same time[J].Metron Int J Statist,2007,65(1):3
[12]Strimmer K.A unified approach to false discovery rate estimation[J].BMC Bioinformatics,2008,9:303
Empirical estimation and application of false discovery rate
WANG Ting1),ZENG Ping1,2),HUANG Shuiping1),ZHAO Huashuo1)1)Department of Epidemiology and Health Statistics,School of Public Health,Xuzhou Medical College,Xuzhou 221002 2)Department of Epidemiology and Health Statistics,School of Public Health,Nanjing Medical University,Nanjing 210029
microarray data;false discovery rate;empirical Bayes;density estimation
Aim:To investigate the empirical Bayesian estimation and application for density,null distribution and false discovery rate in large scale data.Methods:A Bayesian two-group model was constructed for two microarray data,density function was estimated using the method of Poisson regression,and then the empirical Bayes was applied to estimate false discovery rate and local false discovery rate based on the estimated density.Results:The method of Poisson regression for density estimation was an appropriate alternative for the empirical Bayesian estimation for null distribution and false discovery rate.Conclusion:It is feasible to estimate false discovery rate and null distribution empirically by employing the parallel data structure in large scale data.
R195.1
10.3969/j.issn.1671-6825.2012.05.014
*江苏省教育厅高校哲学社会科学研究基金资助项目2010SJB790037;徐州医学院公共卫生学院科研课题资助项目201107,201115
(2011-09-07收稿 责任编辑李沛寰)

