基于小波网络的大坝变形预测分析
张 俊
(澧县水利局澧南分洪闸管理所 常德市 415500)
前 言
水利枢纽在综合利用河流水力资源,比如运输、灌溉、发电等方面具有重要的经济效益和社会效应,大坝作为水利枢纽的重要组成部分,其监控水平直接影响到水利枢纽的安全运行。大坝的监控参数,比如位移、变形等,因受到温度、水位、时效等多种因素影响,呈现高度非线性特点[1-2]。
为了准确地预测大坝参数变化,人们基于回归分析、人工神经网络等方法,构建了相应数学模型。李富强等[3]利用回归分析法判断大坝结构性态的变化趋势,并评估大坝的安全性。龚晓雯等[4]则针对大坝水平位移数据,改进了回归分析模型,提高了模型的预测精度;马丽霞等[5]则采用BP神经网络对某大坝作了变形分析,优化了网络结构,获得了良好的预测效果;田斌等[6]利用人工神经网络模型对进水闸顶位移作了预测,为大坝安全性态的在线监控提供了支持。
不过,不论回归分析模型,还是人工神经网络模型都或多或少存在一些问题,比如:回归分析模型需要提高大量的监测数据,而人工神经网络模型则收敛慢、训练耗时长等。相对而言,近年出现的小波网络,不仅比神经网络有更强的自学习、自适应能力,而且还有时频分析、去噪抗干扰等特点。本文利用小波神经网络理论建立预测模型,并与其他两种模型预测结果进行比较,显现出小波网络预测的优越性。
1 大坝位移参数的特点
从时序关系而言,大坝位移监测数据是一组随时间变化的非平稳信号 s0(t),它由有效信息 s(t)和噪声 n(t)两部分组成:

对于大坝位移的有效信号s(t),研究表明它受温度、库水位以及时间影响[3]~[5]。 即 s(t)由温度分量s1(t)、水位分量 s2(t)和时效分量 s3(t)等。 这些组成信号的频率是不同的,一般认为噪声由于其随机性、突变性较强,呈现出高频特性。温度分量是指由于温度变化所引起的坝体变形,它更多的和天气变化情况有关,更多的表现出中频特性,另外温度分量的效应具有一定的迟滞性,即温度对大坝变形的影响有一定程度的滞后;由库水位所施加的静水压力是大坝主要的荷载,但部分研究认为库水位的二次方、三次方对大坝位移也有一定的影响[4]。由于库水位同样与天气相关,它也呈现中频特性。时效分量则主要是由于大坝在自重和水压等长期作用下所展现出的一种趋势性变形(向上游或向下游),变化异常缓慢,属于低频特性。
由此,大坝位移监测数据可用下式表示:
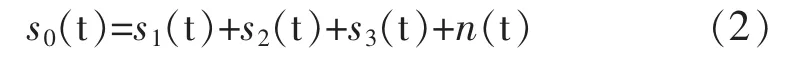
2 小波网络
小波变换克服了傅里叶变换难以准确分析非平稳信号的特点,它通过基本小波函数的平移、伸缩精确的体现非平稳信号的全部信息,在信号分析中应用十分广泛。而小波神经网络则是在则是基于小波分析的良好局部化特性,进而构建的多分辨率人工神经网络,它与BP神经网络类似,只是利用小波函数代替BP神经网络的sigmoid函数作为网络的激活函数,在高度非线性函数逼近方面,具有学习速度快,灵活性好、准确度高等特点。
如图1所示,大坝变形小波网络预测模型由输入层、中间层和输出层组成,其中输入层节点数n为大坝变形影响因子的个数,输出节点只有一个,即大坝变形值,中间层节点数m个,一般m可取6~15个[7]。在模型预测的过程中,小波网络利用小波变化将每个输入量分解为m个分量,分别送入中间层的m个节点,而中间层每个节点的输出值为输入层所有节点对其输出的累加。整个模型的输出,则是中间节点输出与其连接权系数之积的线性和。

图1 大坝变形小波网络预测结构图
若模型选用的小波母函数为Ψ(x),则针对不同的中间节点,通过小波母函数的平移和伸缩构建一组小波函数:{Ψa1,b1(x),Ψa2,b2(x),…,Ψam,bm(x)},其中:
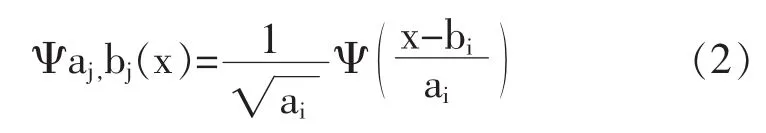
则模型输出为:

上式中,ωi代表中间层第i个节点的输出权值系数,ai、bi分别代表小波函数平移因子和伸缩因子。
小波网络的学习过程主要求解网络参数,即确定ωi、ai、bi三个系数集合,完成网络的构建。其中,小波函数、中间层节点数目以及网络参数求解算法对小波网络学习的速度和精度有较大的影响。关于小波函数的选择,目前尚未形成统一的理论或方法,往往借鉴小波分析中经验来选择,本文选择morlet小波作为小波母函数,它是一种对称、有限支撑的高斯波,已经在模型预测、图像压缩等领域内得到广泛的应用,中间层则通过试算的方法确定为13,网络参数求解算法则采用动量梯度法。
3 实例分析
针对某混凝土大坝10#测点的顺河向水平位移实测资料,选取2010年12月2日到2011年2月1日,共62组数据,如表1所示。在此基础上,分别建立大坝变形的逐步回归分析预测模型、神经网络预测模型和小波网络预测模型,取前55组监测资料作为学习样本,对后9组数据进行预测分析。为了充分考虑大坝变形的影响因素,这里取温度、库水位及其2次方、3次方、时效因素等5个关键性原因作为网络输入层节点,即针对小波网络和神经网络模型均构建5输入节点,13个中间节点和1个输出节点。
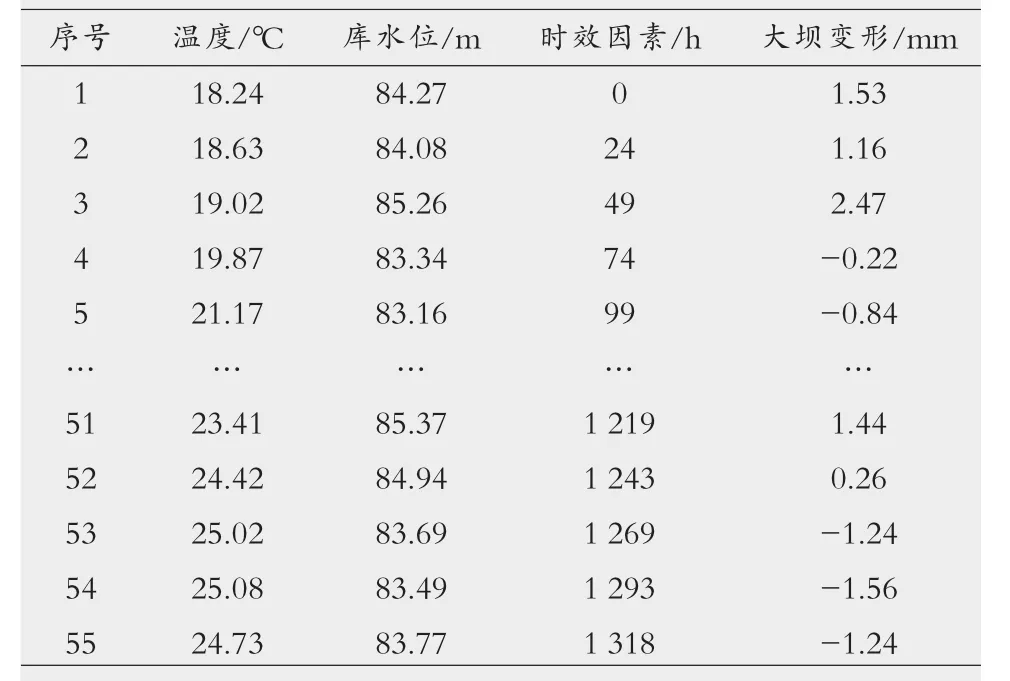
表1 大坝变形监测数据
三种大坝变形预测模型经训练结果如图2所示(前55个节点),三种模型都能够较准确的反应大坝变形趋势。统计样本训练误差表明,逐步回归分析的函数逼近程度较差,最大误差0.55mm,神经网络模型逼近程度较好,最大误差0.09mm,小波网络模型逼近程度最好,最大误差0.06mm。

图2 各种模型预测结果示意图
利用上述训练完成的三种模型,对大坝实测位移数据进行仿真预测,其结果如表2所示。通过表2和图2(后九个节点)可以清楚的看到,小波网络预测模型和逐步回归分析模型的预测结果与实际测试结果相比,不仅变化趋势一致,在波峰、波谷处几乎一致。其中小波网络预测中峰谷处最大误差仅0.1 mm,预测效果很好,完全满足大坝变形预测要求。而神经网络模型虽然样本训练精度角度,但是预测效果却最差。因此,对大坝变形进行预测时,选择小波网络可以得到更好的效果。
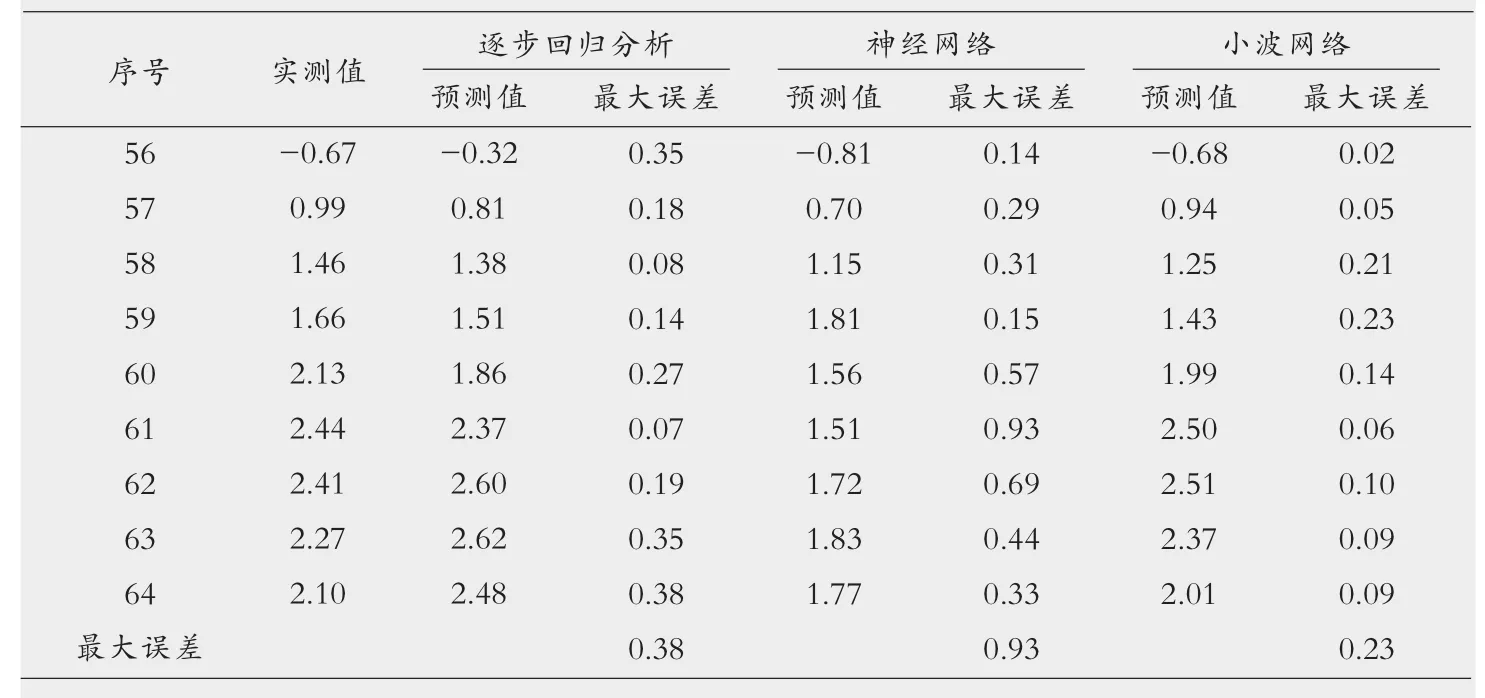
表2 各种模型预测精度一览表
4 结 论
(1)在总结影响大坝变形的关键性因素的基础上,应用逐步回归分析、神经网络、小波理论等数理统计和智能分析方法,建立基于小波网络的大坝变形预测模型,并对其预测效果进行比较,显示小波神经网络模型的预测精度最高。
(2)小波网络实质上是小波变化和神经网络的结合,由于对输入信号采用小波变换方法进行分析,它比逐步回归分析更敏锐的发现影响大坝变形的主要因素,同理也利用了神经网络高度非线性函数逼近能力,使得整个预测的精度较好。为此,小波神经网络在大坝变形分析上具有明显的优越性,完全可以满足对大坝变形预测的要求,对大坝的监测与安全分析具有重要的参考意义。
1 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
2 顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006.
3 李富强,钱镜林.大坝监测数据自回归模型特征根的应用研究[J].浙江大学学报(工学版),2009,43(1),25-30.
4 龚晓雯,范磊.非线性分位点回归方法在大坝安全监测中的应用[J].河海大学学报(自然科学版),2011,39 (1),17-20.
5 马丽霞,王凤艳,陈剑平.基于人工神经网络的大坝变形分析与预报——以西津大坝27#点的变形监测为例[J].2009,39(3),72-75.
6 田斌,任德记,何薪基.隔河岩电站进水闸位移的前馈网络预测模型[J].人民长江,2002,33(11),12-16.
7 赵学智,邹春华,陈统坚,等.小波神经网络的参数初始化研究[J].华南理工大学学报(自然科学版),2003,31(2),65-68.


