应用ABAQUS进行渗流作用下基坑边坡稳定性分析
袁 锋
(湖南省水利水电勘测设计研究总院 长沙市 410007)
引 言
近年来,随着我国城市化建设发展步伐的加快,国内深基坑工程越来越多,大量的实践工程显示,渗流问题是许多基坑工程事故的主要原因之一,在基坑稳定分析中渗流计算不能忽视。
当存在渗流作用时,工程上一般采用将地下水的作用考虑成沿滑裂面上施加孔隙水压力[1]来粗略的计算。而在实际基坑工程中,渗流场地分布十分复杂,利用简化方法仅在少数情况下可以应用,当水头差较大或采用排水措施时,渗流力的不利作用随之增大,简化方法计算结果往往脱离实际,甚至错误。
基坑的渗流计算属于具有渗流自由面无压渗流计算,且渗流自由面不断变动,加之渗流场有不同程度的非均质和各向异性、边界条件复杂,在数学上求得解析解是非常困难的。随着电子计算机的普及和数值计算方法的发展,特别是有限单元法提出后,推动了渗流数学模型的发展,为渗流计算提供了有效的方法[2]。
本文在利用强度折减[3]有限元法进行基坑稳定分析与渗流场的计算时采用统一的有限元单元和节点,利用稳定渗流作用下的单元渗透节点力,再施加到基坑稳定分析中去,得到稳定安全系数。这种方法考虑了土体的弹塑性本构关系,渗流对稳定的影响,跟踪土体内塑性区的展开情况,模拟边坡的失稳过程及滑裂面的形状,适用于任意复杂的边界条件。
1 ABAQUS程序简介
ABAQUS是由美国HKS公司开发的非线性有限元分析软件[4],是世界上先进的大型通用有限元分析软件之一;其解决问题的范围从相对简单的线性分析到许多复杂的非线性问题,在材料、几何与接触非线性方面的分析能力方面有较好的适用性,以高求解效率和高计算精度在工程界享誉盛名。因能方便地解决岩土力学中复杂的非线性问题,故ABAQUS在岩土工程分析中得到了广泛的应用。
2 渗流有限元与强度折减法的结合
2.1 渗流力作用原理
水体在土粒骨架之间的孔隙中发生流动,会产生对土体和土粒骨架的稳定有一定的破坏作用[5]渗流。渗流作用在颗粒表面的力有两种:即垂直于颗粒周界表面的水压力和颗粒表面相切的水流摩阻力。显然,这两个力经过对颗粒表面积分,都可用一个向量代表,如图1(c)中f0p与f0f,这两个力的合力f0可称为渗流作用力。

图1 颗粒上的渗流作用力图
考虑体积为V的土体的渗流作用力为:

从计算的方便起见,将这个力f分解为铅直向上的分布与沿流线的分布。如图2所示,也就是分解成浮力u和渗透力fs。如图3所示,考虑沿流线方向任一土柱的静力平衡可得:
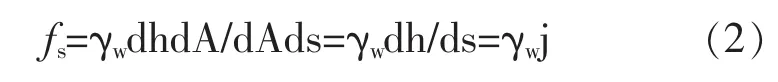
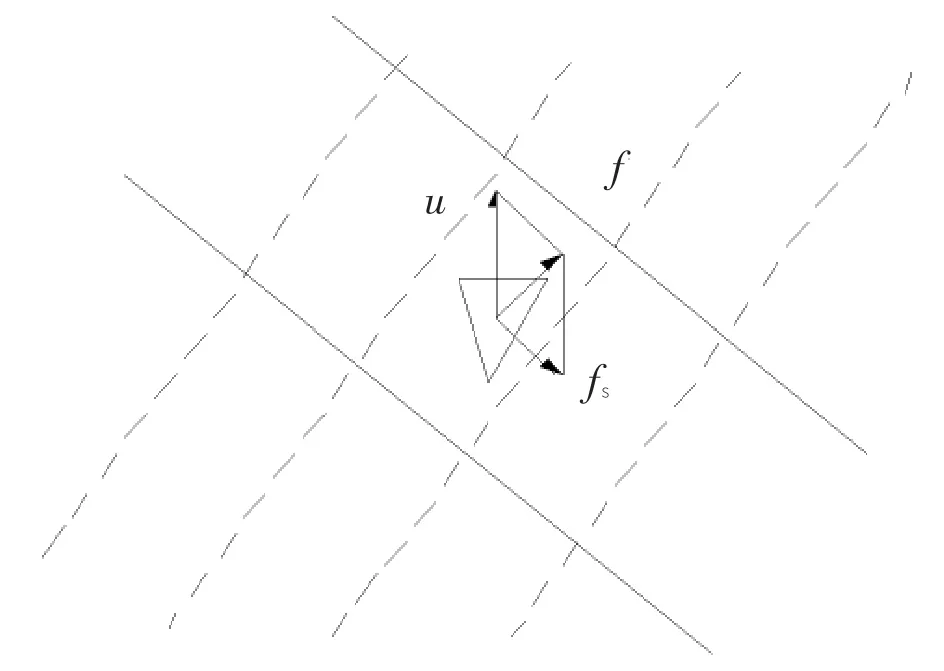
图2 渗流作用力的分解

图3 土柱周边的静水压力关系
式中J——水力坡降;
γw——水的容重。
考察上面渗透力式(2)的来源,可知是由水流的压力转化为体积力,图3所示的压力水头差这个外力包括两部分,即dh+dz,其中dh可理解为渗流水头,dz为静水头;而另一个外力为倾斜流管的自重分力水头(-dz),正好与压力水头中的静水头dz相平衡,只剩下一个渗流水头dh产生水的渗流作用。同时土柱周边的静水压力,只对土体起一个浮力的作用,使土体转化为浮重。因而从这些力的关系可知,水作用于土体的力可以渗透力与浮力形式表示;或以土体周边的水压力形式表示。这个概念很重要,使我们不致重复考虑水流的作用力。本文用有限元法求解单元渗透力然后参与到基坑整体稳定的平衡分析中正是以这种理论为基础的。
2.2 有限元强度折减法的原理
强度折减法就是在理想弹塑性有限元计算中,将边坡土体抗剪强度参数逐渐降低,直到其达到极限状态为止,同时得到边坡的强度储备安全系数Fs。于是有:

式中c、j——土体有效黏聚力和有效内摩擦角;
cf、jf——与强度储备安全系数Fs所对应的有效黏聚力和有效内摩擦角。
强度折减法不需要对滑动面形状和位置做假定,通过逐步折减强度参数使边坡达到极限平衡状态,此时,所对应的折减系数就是边坡的稳定安全系数Fs。
在ABAQUS软件中,材料参数是可随场变量而变化的,利用此功能可以简单的实现强度参数减小的过程。具体操作为:首先定义一个场变量,通常就取其为强度折减系数Fs,同时定义随场变量变化的材料模型参数;在分析开始指定场变量的大小,并对模型施加重力(体力)荷载,建立应力平衡状态,最后在后续的分析步骤中线性增加场变量Fs,计算终止后对结果进行处理,按照极限状态评价标准对边坡进行稳定性分析,确定边坡的安全系数。
在本文的有限元计算中采用岩土工程中最常用的MC准则作为屈服准则,控制点的水平位移发生突变时的所对应的状态作为临界失稳状态,此时与之相对应的折减系数作为基坑的整体安全系数。
2.3 实现过程
本文利用ABAQUS有限元软件进行渗流有限元分析,得到了稳定渗流期的各单元节点水头,并根据水力梯度矢量计算出渗透力;利用ABAUQS软件实现强度折减得到重力、浮力以及渗透力作用下的基坑整体稳定性。计算结果表明,采用此方法进行实际的工程稳定分析是合理的。
3 算例分析
以某工程基坑为例采用本文方法结合验算其边坡稳定性。基坑几何尺寸及土性指标如图4所示。采用有限元法计算渗流场,并将单元渗透力参与强度折减分析中。为了便于对照分析,同时给出忽略渗流力作用的强度折减法、简化的Bishop法计算结果如附表所示。图5为基坑有限元网格划分。渗流场计算部分图形输出为图6~图7,强度折减有限元计算结果见图8~图11。

图4 基坑几何尺寸及土性指标
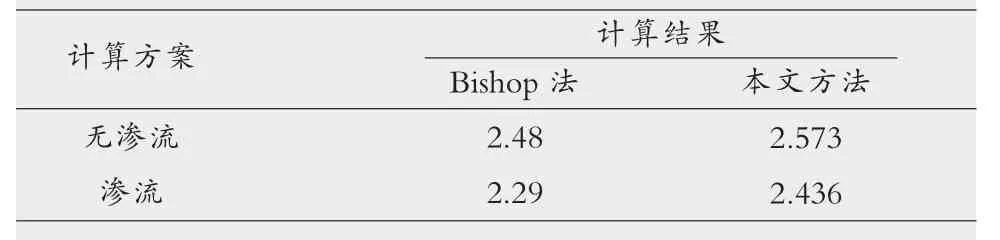
附表 渗流力计算结果比较

图5 基坑有限元网格划分 (单位:m)

图6 渗流等势线分布图 (单位:m)
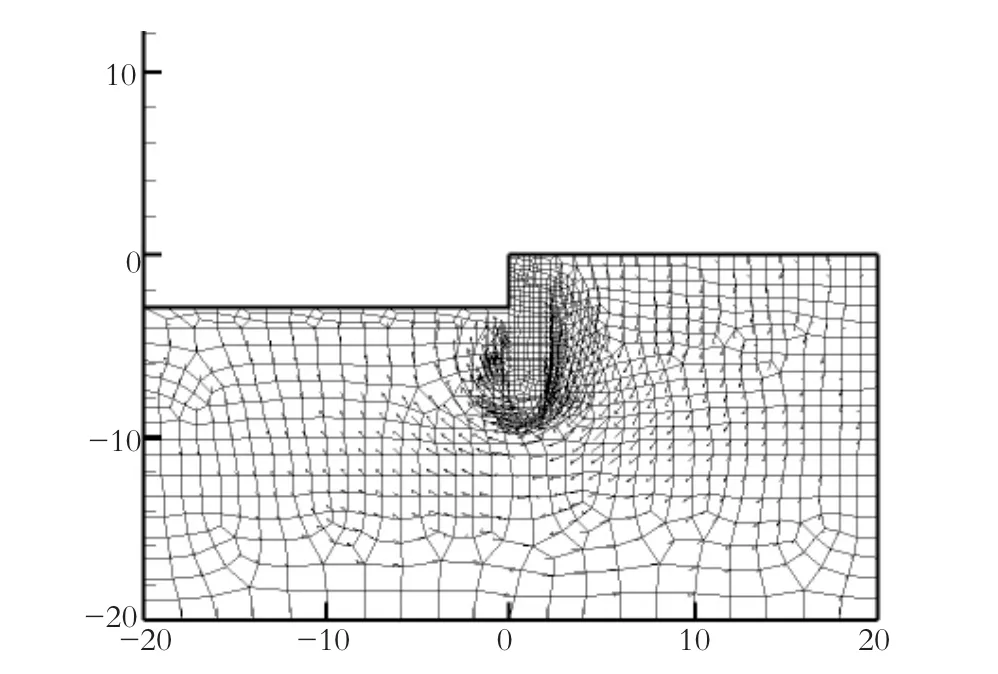
图7 渗透力矢量分布图 (单位:m)

图8 坡顶水平位移与安全系数Fs的关系
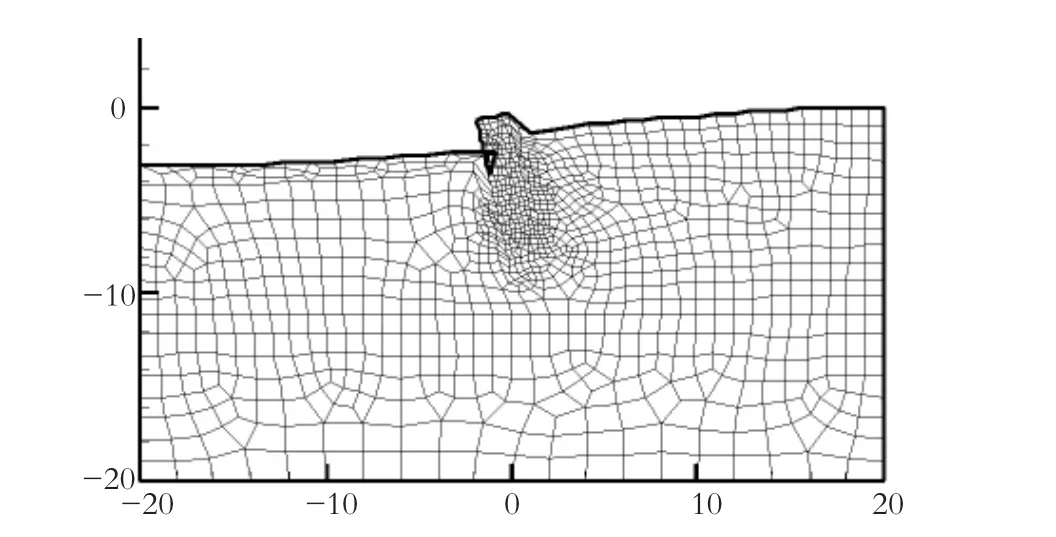
图9 考虑渗流时基坑变形网格

图10 考虑渗流时增量位移等值线图
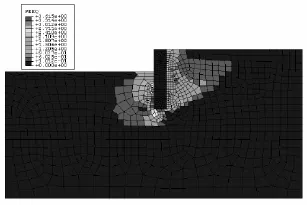
图11 考虑渗流时临界状态下的等效塑性应变图
由附表可见,上述两种方案计算所得的安全系数均高于Bishop法计算结果,两者差别在3%~6%之间。这一结果与张鲁渝等[6]认为的在一般稳定分析中有限元强度折减系数法所得稳定安全系数比简化Bishop法平均高出约5.7%的结果非常相近。
图8给出了采用本文方法计算的基坑顶节点水平位移与安全系数Fs的关系曲线。图中水平位移在折减前(分析步Fs<1)因为受到自重与渗流作用的影响,基坑顶节点水平位移出现向基坑面发展的趋势;折减开始后(分析步Fs>1),由于土体强度参数的降低,基坑顶水平位移明显地倾向基坑,在最后的破坏中甚至出现了向上游倾倒的现象(图11)。取基坑顶水平位移突变时对应的强度折减系数作为整体安全系数,从图8中不难看出来,不考虑渗流作用时候位移突变发生的比较明显,按边坡失稳的判别标准取此时的安全系数为2.573,而在考虑渗流的曲线中,位移突变不是很明显,取最大曲率对应的安全系数,此时安全系数为2.436。从图10、图11中还可看出,临界破坏时基坑的位移与变形发展情况,同时也能比较直观、清晰地评判出临界破坏面的位置和形状。
本文的算例中基坑的挖深较小,渗流作用仅考虑水在自重作用下的稳态渗流。而在实际的深基坑工程中,常常采抽水措施,渗流力的不利作用随之增大,简化方法的Bishop法在计算渗流作用下的稳定安全系数的时候,无法考虑时态渗流的缺点将进一步地放大,计算结果与实际情况会有很大的差异,甚至错误,用错误的计算结果指导工程实践将是十分危险的。而用有限元计算渗流场,不仅可以考虑潜水渗流,而且可以考虑承压水引起的渗流场变化。有承压水存在时,可以将承压含水层作为渗流场计算时的已知水头边界条件,也可以将潜水渗流和承压水渗流引起的渗流场分别计算,然后二者叠加得到最终流场分布。基于这种叠加原理,就可以将多种渗流情况和复杂边界的渗流计算分解为多个简单的渗流场分别加以计算,然后叠加得到合渗流场分布。这对于边界条件复杂的基坑边坡来说是十分有效的。
4 结 论
本文提出利用ABAQUS程序实现渗流作用下的基坑稳定性分析,简单地介绍了渗流有限元与强度折减法的结合和具体实现过程,通过某工程基坑进行计算分析,并与简化的Bishop法计算结果进行对比。计算结果表明本文方法在验算基坑边坡稳定性不仅可以利用长期工程实践的经验,而且在边界条件较为复杂的渗流场计算中有其独到的优越性。
1 张孟喜,陈炽昭.土坡稳定分析的有限元追踪法[J].岩土工程学报,1991,13(6).
2 钱家欢,殷宗译.土工原理与计算(第二版)[M].北京:水利电力出版社,1994.
3 ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique, 1975, 25(4):671-689.
4 ABAQUS.Standard User's Manual[M].Hibbitte Karlsson&Sorenson INC,2002:26-78.
5 李广信.高等土力学[M].北京:清华大学出版社,2002.
6 张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,(1):21-27.

