基于增量Kalman滤波的GPS多路径效应系统误差研究
伍锡锈
(广州市城市规划勘测设计研究院,广东 广州 510060)
GPS高精度定位应用中,多路径效应误差是一个最主要的误差来源,近年来很多对GPS接收机信号处理的方法,如窄相关技术、多路径消减技术等都可有效地消减多路径效应的影响,但是其残余多路径效应误差对高精度GPS应用仍具有很大的影响,且由于其本身的复杂性,所以该研究一直以来均是GPS数据处理研究的热点。多路径效应误差其主要表现为系统性误差,但是其特性复杂,既具有延续性,又具有偶然性,因而很难用统一的确定的模型来准确描述它。目前,对于该类系统误差通常采用的方法是将其视为平差模型的模型误差,利用函数模型或随机模型或二者之间综合作用来予以补偿,从整体上减弱或消除其影响,以保证平差结果的高精度。具体有以下几种:附加系统参数的参数平差法、附加系统权法、附加系统参数和系统法、选群拟合法和半参数法[1-4]。
Kalman滤波方法是一种从带有噪声干扰的信号中提取有用信号的参数最优估计方法,目前广泛应用于信号处理和导航定位等领域,并经过诸多学者的研究和改进发展了一系列的滤波方法,包括扩展Kalman滤波、抗差自适应Kalman滤波、粒子滤波等等[5-8]。但是,Kalman滤波最优估计是建立在动态噪声和观测噪声均为白噪声的假设条件下推得的一种递推滤波方法,即观测不含系统性误差影响。在GPS高精度定位应用中,由于多路径效应系统误差的干扰,将会很大程度上影响Kalman滤波估计值的精度和可靠性,乃至使滤波结果发散,但是实际应用中相邻2个观测向量的系统误差大小比较接近,即认为在较短的观测时间段内,观测系统误差有微小的变化,那么相邻观测向量之差即观测向量增量中所含的系统误差较小,其能够满足Kalman滤波观测噪声为白噪声的假设条件。从而在本文中对利用观测向量的增量Kalman滤波极其在GPS多路径效应系统误差的应用进行研究。
1 增量Kalman滤波
在标准Kalman滤波中设系统状态方程和观测方程分别为

式中:Xk为状态向量,Φk,k-1为状态转移矩阵,Lk为观测值向量,Ak为设计矩阵,Wk和ek均是均值为0且协方差矩阵分别为∑Wk和∑k的正态白噪声。假设ΔLk=Lk-Lk-1为观测向量增量,则增量Kalman滤波的增量观测方程可以表示为

其中:vk=ek-ek-1,由于诸多实际中相邻观测向量Lk和Lk-1的测量系统误差大小比较接近,所以ΔLk的系统误差相对较小,并假设其服从均值为0协方差矩阵为Rk的正态白噪声。
增量Kalman滤波的状态向量Xk的最佳估值可以由下面一组递推公式实现:
1)计算预测状态向量:

2)计算预测状态协方差矩阵:

3)计算信息向量:

4)计算增益矩阵:

5)计算新的状态估值:
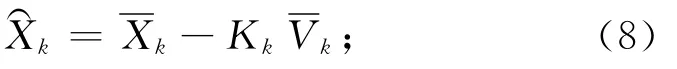
6)计算新的状态向量协方差矩阵:

经过该递推公式实现的增量Kalman滤波估计,其得到的状态估计具有无偏性,即E()=E(Xk),具体可参考文献[9]。
2 实例计算分析
试验地点选在香港理工大学的教学楼上,基准站使用Topcon双频接收机,天线类型为Topcon CR3扼流圈天线,流动站为Septentrio接收机和普通测地型天线,基线长度约3.997m,数据采样频率为1Hz,测站周围有较多的玻璃幕墙高楼,多路径效应影响比较严重。数据预处理过程如下:首先通过对较长时间的静态观测解算得到基线向量信息;然后利用该基线先验信息逐历元解算出测点的动态轨迹,从而得到局部坐标系下相对于该基线信息的三维坐标残差序列,解算软件为GPSSM软件[10]。由于基线距离非常短,在双差观测方程中,卫星钟差和接收机钟差能够比较好地得到消除,电离层、对流层、卫星轨道误差影响可以被忽略,其主要误差来源为多路径效应和接收机的高频噪声。下面从中提取X方向100min的观测数据进行处理,为对比分析本文方法处理效果,现采用2种方案分别进行处理。方案1:标准Kalman滤波方法,处理效果如图1所示;方案2:增量Kalman滤波处理方法,处理效果如图2所示。分别绘出滤波处理前后的观测残差序列图、观测向量增量坐标序列图(见图3)和误差统计结果见表1,图1中RAW表示为滤波处理前的坐标序列数据,SKF、IKF分别表示为经过标准Kalman滤波和增量Kalman滤波处理之后的坐标序列。

表1 误差统计结果 mm

图3 观测向量增量坐标序列

从计算结果可以看出:
1)观测残差中不仅含有较强的偶然噪声,而且还含有比较严重的多路径低频系统性误差。
标准Kalman滤波对于观测误差中的偶然噪声具有较好的去噪作用,但是对于其中的系统误差的作用效果较小。
2)从图2和误差统计结果可以看出增量Kalman滤波能够比较有效地消除多路径效应系统误差的影响,从而提高滤波精度,证明本方法具有一定的可行性和有效性。
3)图3中可以看出,相邻2个量测向量的测量观测系统误差大小比较接近,其增量向量所含的系统误差相对很小,并且其更能够满足Kalman滤波所假设的观测向量服从相互独立、期望为零的高斯分布条件。
3 结束语
在实际应用中尤其是对于短基线,在双差观测方程中,卫星钟差和接收机钟差能够比较好的得到消除,电离层、对流层、卫星轨道误差影响可以被忽略,其主要误差来源为多路径效应和接收机的高频噪声,而相邻观测历元多路径误差相差较小,从而利用增量Kalman以提高滤波估计的精度和可靠性,以及本文方法对于该类型的系统误差具有较好的处理效果,并且计算简单,便于工程应用。
[1]李万年,王振杰.基于半参数模型的高精度GPS基线处理中系统误差的分离[J].山东理工大学学报:自然科学版,2005,19(6):18-24.
[2]王振杰,卢秀山.利用半参数模型分离GPS基线中的系统误差[J].武汉大学学报:信息科学版,2007,32(4):316-318.
[3]欧吉坤,王振杰.精密测量中系统误差的分离方法[J].数据采集与处理,2003,18(4):365-368.
[4]周江文.系统误差的数学处理[J].测绘工程,1999,8(2):1-4.
[5]杨元喜,张双成.导航解算中的系统误差及其协方差矩阵拟合[J].测绘学报,2004,33(3):189-194.
[6]杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.
[7]Yang Y,He H,Xu G.Adaptively robust filtering for Kinematic geodetic positioning[J].Journal of Geodesy,2001,75(2):109-116.
[8]Yang Yuanxi,Xu Tianhe.An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components[J].The Journal of Navigation,2003,56(2):231-240.
[9]傅惠民,吴云章,娄泰山.欠观测条件的增量Kalman滤波方法[J].机械强度,2012,34(1):43-47.
[10]戴吾蛟.GPS精密动态变形监测的数据处理方法研究[D].长沙:中南大学,2007.

