基于K－L特征提取与支持向量机的油浸式变压器故障诊断模型研究

方 飚

(四川省电力工业调整试验所，四川成都 610072)

变压器是电力系统中的重要设备，其运行状态直接影响到系统的安全性。油中溶解气体分析(dissolved gas analysis，DGA)是目前诊断充油电气设备故障的重要手段，已作为变压器内部潜伏性故障的主要试验项目列于DL/T 596－1996变压器试验项目的首位［1］。DGA往往能够较准确、可靠地发现逐步发展的潜伏性故障，防止由此引起重大事故。近年来的研究已将各种人工智能技术如神经网络、粗糙集、聚类算法、支持向量机等引入到变压器的故障诊断当中。

支持向量机算法［2－5］是在统计学理论基础上发展起来的一种新的模式识别方法。它是由Vapnik等人于1995年提出的从统计学习理论发展出的一种模式识别方法，是目前较为流行的适用于小样本训练的大边缘分类器。

K－L变换是经典的传统方法，适用于任何概率分布，它能保留原样本中方差最大的数据分量，所以K－L变换起了减小相关性、突出差异性的效果，因此是在均方误差最小的意义下获得数据降维的最佳变换。

这里针对变压器的5种运行模式(4种故障模式与1种正常运行模式)提出了建立基于支持向量机与K－L特征提取技术的变压器故障诊断模型。该模型的基本思想是在训练数据预选取阶段采用基于Mercer核函数的欧式距离的查询策略选取最能代表各类的样本数据，从而能够更加准确地构造SVM分类器，减少训练样本数和缩短训练时间。同时利用K－L变换的特征提取技术在系统分类精度不降低的情况下将样本数据由六维降到三维，提取了样本数据集的特征值，同时通过三维图表示了降为三维的样本数据，从而为进一步提高分类正确率奠定了基础。

1 支持向量机分类原理

1.1 线性情况

当训练样本集线性可分时，分类超平面的描述为

式(1)中，向量ω为分类超平面的权系数;b是分类阈值。最优分类超平面可通过解下面的凸二次优化问题获得。

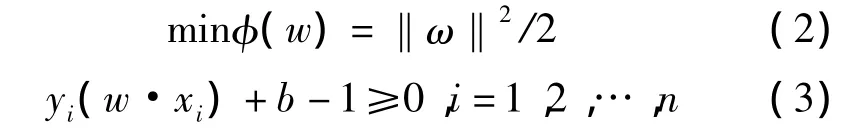
通过求解，得到最优分类超平面的分类判别函数为

其中，αi为拉氏乘子，拉氏乘子不为0的解向量为支持向量。

1.2 非线性情况

对于非线性问题，SVMs通过选择适当的非线性变换，将输入空间X中的训练样本映射到某个高维特征空间F，使得在目标高维空间中这些样本线性可分。根据泛函的有关理论，若核函数K(x，xi)满足Mercer条件，则对应某一变换空间中的内积〈φ(xi)·φ(x)〉，函数φ∶x→F是一个从非线性输入空间X到高维特征空间F的映射，所以求映射φ∶x→F只要知道如何由输入x、xi计算内积〈φ(xi)·φ(x)〉即可，由

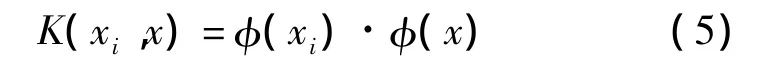
将式(4)重写，即可得到对应高维空间的分类函数为

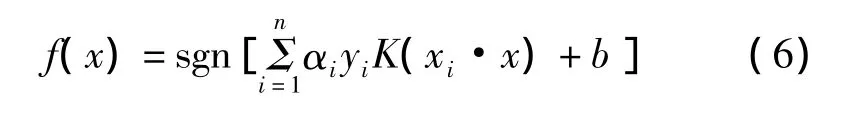
2 核距离与K－L变换

根据SVM分类原理，经向量化处理的变压器DGA数据可直接作为训练样本数据，但此方法使得SVM训练算法速度比较慢，这是因为训练样本的数量决定了二次规划问题目标函数中矩阵的维数，使得求解规划问题的速度与维数呈指数增长。为了提高训练速度，减少学习样本数，缩短训练时间，则采取主动选择对于确立分类器最重要的新样本进行训练，来进一步设计新的分类器，从而使得可以用尽可能少的标注样本数来实现较高的分类精度。

支持向量机学习算法包括两个独立的部分＜c，f＞，c是一个SVM多类分类器，f是一个查询函数，决定应从候选集中选择哪些样本进行训练。由于检测变压器运行模式是一个多分类的模式识别问题，因此在这里SVM分类器采用的是1－a－r方法。这里通过引λ类质心和基于Mercer核函数的欧式距离等概念来定义查询函数f。其查询策略是通过调节基于Mercer核函数欧式距离的选择范围来选择最能代表各类的样本数据。这种策略最大程度地缩减了训练样本数据，降低了算法的运算量。

2.1 基于Mercer核函数的欧式距离

Mercer核函数的原理是将输入样本数据空间非线性映射到新的特征空间。

芦晓飞表示，有机农业替代化学农业成为当前农业转型升级的主要出路，利用土壤微生物技术是当前撬动我国农业可持续发展、提高农产品质量的有力杠杆。奥特奇具备技术优势主要体现在以下三个方面：一是独一无二的酶制剂保障土壤健康；二是领先的有机矿物元素技术为植物提供充足的营养；三是独特的微生物提取物和植物抗诱剂技术促进农作物健康生长，重建土壤健康生态。

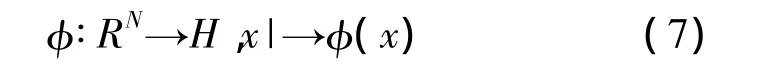
样本数据空间中的欧式距离在新的特征空间H里可以表示为

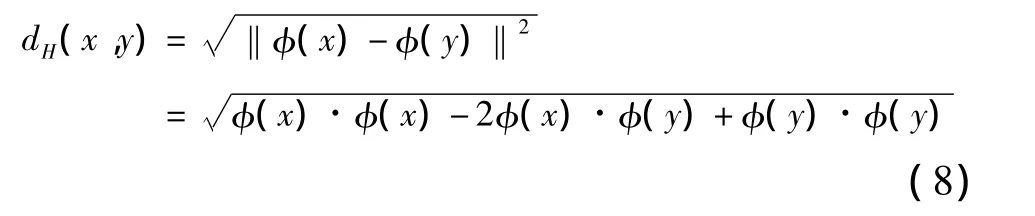
根据Mercer核映射φ的性质，输入空间的点积在新的特征空间H中可以用Mercer核函数来表示，即

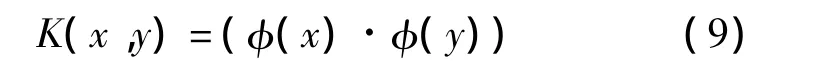
由式(7)和式(8)可以表示为

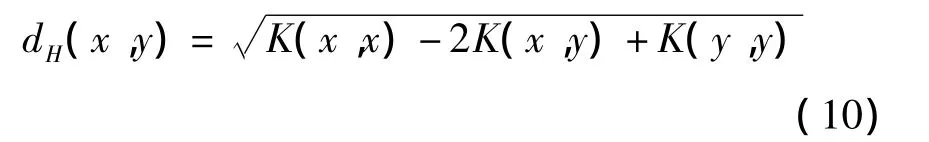
2.2 基于K－L变换的特征提取

K－L特征提取［6］是通过映射(或变换)的方法把高维特征向量变换为低维特征向量。通过特征提取获得的特征是原始特征集的某种组合，即A∶Y→X，可见，新的特征中包含了原有全体特征的信息。特征提取的关键问题是求出最佳变换矩阵，使得变换后的m维模式空间中，类别可分性准则值最大。

设x为n维随机向量，x可以用n个正交基向量的加权和来表示为

式中，αi为加权系数;φi为正交基向量，满足

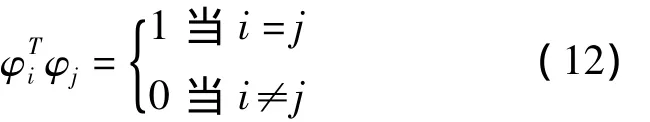
从n个特征向量中取出m个组成变换矩阵A，即 A=(φ1，φ2，…，φm)(m ＜ n)，这时，A 是一个 n ×m维矩阵，x为n维向量，经过ATx变换，得到降维为m的新向量。通过选取m个特征向量构成变换矩阵A，使降维的新向量在最小均方误差准则下接近原来的向量x。

对于式(12)现在只取m项，对略去的项用预先选定的常数bj来代替，这时对x的估计值为

由此产生的误差为

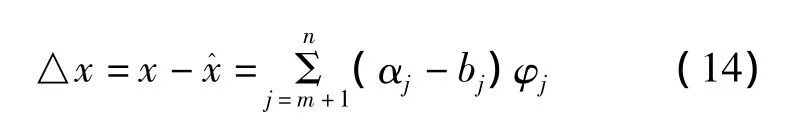
均方误差为

式中，λj是x的自相关矩阵R的第j个特征值;φj是与λj对应的特征向量。显然所选的λj值越小，均方误差也越小。

综上所述，基于K－L变换的特征提取的步骤如下［6］:(1)平移坐标系，将模式总体的均值向量作为新坐标系的原点;(2)求出自相关矩阵R;(3)求出R的特征值λ1，λ2，…λn及其对应的特征向量φ1，φ2，…，φn;(4)将特征值从大到小排序，如 λ1≥λ2≥…≥λm≥…≥λn，取前m个大的特征值所对应的特征向量构成变换矩阵 A=(φ1，φ2，…，φm);(5)将n维的原向量变换成m维的新向量y=ATx。

利用K－L变换方法完成了对输入样本的特征值提取，降低了输入样本维数，使SVM能够快速分类。

3 故障诊断流程

(3)对得到的每类基于核函数的欧拉距离按一定序列排序。如低温过热故障所得的基于核函数的欧拉距离采用降序排列;而高温过热故障所得的基于核函数的欧拉距离采用升序排列。

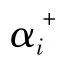
(5)得到的5类数据集即可作为训练集。

(6)通过K－L变换对所选取的训练集进行特征提取，将其降为三维以降低运算量。

(7)将测试数据代入训练好的分类器中进行试验，如果测试误差较大，返回步骤(3)。

(8)达到精度即可作为故障分类器。

4 变压器故障诊断及分析

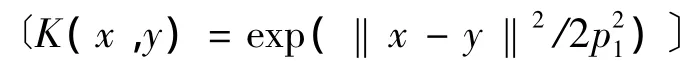
通过所提学习方法选取29例正常模式、12例低能放电模式、8例低温过热模式、9例高温过热模式和20例高能放电模式训练样本组成训练集。同时与通过传统学习方法随机选择等量的样本数据作为训练集进行比较，测试数据如表1所示。

图1是训练集的相对位置关系图。图中实线表示正常运行模式，虚线表示高能放电模式，星号表示低能放电模式，加号表示高温过热模式，棱形表示低温过热模式。从图中可知，所得的训练集的三维图正确地反映了油浸式变压器实际的运行模式。高能放电模式样本数据与低能放电模式样本数据位置紧密但较易区分;而高温过热模式样本数据与低温过热模式样本数据混淆严重，由此推断，这两种故障模式较难区分。表1显示了两种方法训练的分类器对测试数据正确诊断率的仿真结果。同时为检验参数寻优对分类结果的影响，对基于经验选取参数(p1=0.1，C=100)的多类SVM模型与基于最优参数的多类SVM模型的分类结果进行了对比。

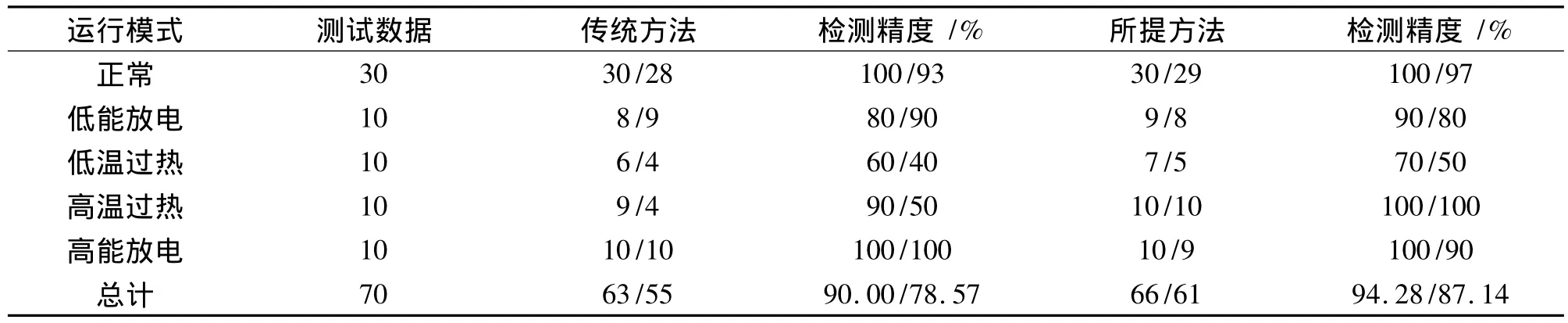
表1 两种方法诊断的结果对比

图1 训练集三维图

从表1对测试样本的检测率可知，通过所提方法获得的训练集构造的分类器比传统方法构造的分类器更精确。因此故障诊断正确率更高。同时可知通过寻优所得的基于最优参数的故障诊断模型比基于经验的参数模型具有更高的检测正确率。

通过对变压器油中气体容量(×10－6)的现场测试，具体值为:φ(H2)=127，φ(CH4)=107，φ(C2H2)=244，φ(C2H4)=154，φ(C2H6)=11，φ(CO)=174.通过所提方法建立的诊断模型，诊断结果为高能放电。通过实际的检测，故障是由于次级线圈放电从而造成整个线圈的损坏。

5 结论

提出了将支持向量机学习算法与基于K－L特征提取技术应用于变压器故障诊断模型的新算法。通过主动选择各类数据集中能正确代表各类相对关系的样本数据来训练分类器，因此提出的主动学习方法能够在缩减训练样本和计算量的情况下仍能达到传统方法的检测精度。同时引入了基于K－L变换的特征提取技术，使能够实现样本数据从六维降到三维，并通过Matlab作图将其显示在三维图中。实验表明，采用所提方法相对于传统方法具有更高的故障诊断率。在仿真实验中，分类的准确度与核函数类型的选择和相应参数的选取密切相关，因此下一步工作是从SVM的分类机理出发对模型的参数选择与精确度的提高可以展开进一步的研究。

［1］DL/T 596－1996，电力设备预防性试验规程［S］.

［2］Warmuth M K，Liao J，Ratsch G et a1.Active Learning with Support Vector Machines in the Drug Discovery Process［J］.Journal of Chemical Information and Computer Sciences，2003，43(2):667 －673.

［3］Hsu C W，Chang C C，Lin C J.A Practical Guide to Support Vector Classification［Z］.2003 － 07.http://www.csie.ntu.edu.tw/cjlin/papers/guide/guide.pdf.

［4］Wang Liguo，Zhang Ye，GU Yanfeng.The Research of Simplification of Support of Structure of Multi－class Classifier Vector Machine［J］.Journal of Image and Graphics，2005，10(5):572 －574.

［5］Cortes C，Vapnik V.Support Vector Networks［J］.Machine Learning，1995，20(1):273－297.

［6］肖建华.智能模式识别方法［M］.广州:华南理工大学出版社，2006.

［7］Wilson D R，Tony R M.Improved Heterogeneous Distance Functions［J］.Journal of Artificial Intelligence Research，1997，6(1):1－34.

［8］段丹青，陈松乔，杨卫平.基于SVM主动学习的入侵检测系统［J］.计算机工程，2007，33(1):153－155.

［9］Vapnik V.An Overview of Statistical Learning Theory［J］.IEEE Transactions on Neural Networks，1999，10(5):988－999.

［10］Cui Jiang，Wang You－ren.Analog Circuit Faults Diagnosis Based on Clustering Preprocess and SVM［J］.Computer Applications，2006，26(8):1977 －1979.