一种空间负二项回归模型及其应用*
张春霞 蒋红卫 尹 平
传统的统计分析方法通常是建立在独立观测值假定基础上的。然而,在遇到空间数据时,独立观测值在现实研究中并不是普遍存在的〔1〕。对于具有地理空间属性的数据,一般认为在空间上,离得近的变量之间比离得远的变量之间具有更加密切的关系〔2〕。随着遥感技术、地理信息系统和全球定位系统渗透到公共卫生研究各个领域之中,空间测量技术在卫生研究中得到了广泛的应用,空间统计学正在逐渐成为卫生研究领域的热点〔3〕。
由于空间相关性的存在,传统的计数回归模型难以较好地处理具有空间聚集性的数据,经常出现模型拟合精度不高,过度离散或离散过小等情形。较典型的是,作为血吸虫唯一中间宿主——钉螺的空间分布格式研究中,除了草丛密度,温度等因素的影响之外,钉螺的分布往往具有明显的空间聚集特性。苏德隆早在1963年提出水网型钉螺空间服从负二项分布规律〔4〕。但是,也有研究者认为钉螺空间分布并不服从单一的负二项分布〔5-7〕。由于存在大量因素影响钉螺的空间分布,仅仅通过强行拟合负二项分布,无法较好地解决钉螺空间分布与预测等问题,因而,为了解决此类存在空间相关性的数据分析问题,必须引入空间计数回归模型。本文将在引入空间数据形式的基础上,系统地研究空间负二项回归模型及其参数估计,并利用钉螺小范围的空间分布实例研究以说明空间负二项回归模型。
空间数据基本结构
空间数据主要包括三个部分:
(1)空间位置:s1,s2,…,sn;
(2)反应变量:Y(s1),Y(s2),…,Y(sn);
(3)解释变量:X(s1),X(s2),…,X(sn)。
其中,空间位置通常为二维空间域,si=(,)∈D⊂R2,与分别为空间位置的横坐标与纵坐标,可
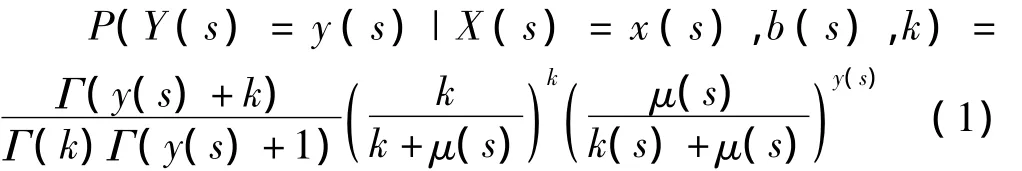
其条件均值为E(Y(s)|b(s))=μ(s),方差V(Y(s)|b(s))= μ(s)+μ(s)2/k。
(3)连接函数

(4)回归模型形式以为离散型变量,也可以为连续型变量;反应变量Y与p维解释变量X={X1,X2,…,Xp}对应于每一个空间位置,表示区域化的反应变量与解释变量。
空间负二项回归模型
空间负二项回归给定以下四个基本假定:(1)反应变量服从负二项分布;(2)反应变量的期望值通过自然对数变换后,与各解释变量之间呈线性关系;(3)回归系数在所研究的空间区域内具有一致性(即为常数);(4)空间随机部分呈高斯平稳过程。根据这四个基本假定,构建如下空间负二项回归基本模型,用于反映空间数据的特征与变化规律。
1.回归模型形式
假定{b(si),si∈R2},i=1,2,…,n 为潜在的不可观测的空间随机过程。其中,b(si)表示空间位置Si上无法被解释变量所能解释的随机部分。空间负二项回归模型可定义如下:
(1){b(s),s∈R2}是一个高斯平稳过程,具有期望E(b(s))=0,方差 -协方差函数 cov(b(s+h),b(s))=C(h),其中,s,h∈R2,方差函数 C(h)=C(θ),θ∈Rv,既是距离的函数,又是方向的函数,但对于高斯平稳过程,其必须满足二阶平稳性与各向同性。
(2)每个位置上的反应变量{Y(s),s∈R2},条件依赖于高斯平稳过程{b(s),s∈R2},即反应变量的概率密度函数为
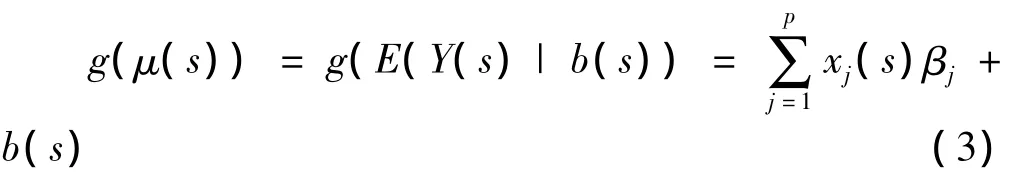
2.参数估计
采用最大似然法来估计空间负二项回归模型的参数。假定高斯平稳过程依赖于正态各向同性协方差函数
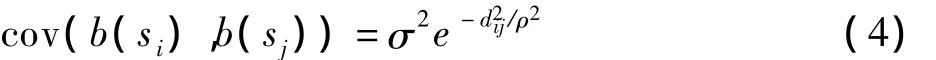
根据空间负二项回归模型的设定,其似然函数为

将相应的分布函数代入公式(5)中,可以获取似然函数最大时各参数的估计。由于上式相当复杂,是高维的非线性积分函数,直接求解极为困难,因此,采用蒙特卡罗最大似然法(MCML)〔8-9〕来进行参数估计。在蒙特卡罗最大似然法中,常采用Gibbs抽样的方法,具体计算可在WinBUGS软件下进行。按照空间负二项回归模型编写程序(见附录),给定待估计参数的先验(理论上,通常应采用无信息先验,但鉴于winBUGS中dflat()函数易导致复杂模型难以收敛的问题,各参数的具体设定见附录中的 winBUGS程序),就可以对待估计参数及其可信区间等统计指标加以估计。首先,通过SAS9获得常规负二项回归模型回归系数的估计值μβi及其标准误σβi;其次,令回归模型参数初始值服从正态分布N(μβi,100*σ2βi),随机取值,获得50组回归系数初始值;其次,采用Gibbs抽样法,迭代20000次,其中前5000次作为预热,对后15000次作为待估参数后验分布的模拟,使用50组参数初始值,从而,获得50条MCMC链,利用方差比法,判断MCMC链是否收敛;最后,合并各链后15000次迭代数据,得到空间负二项回归模型的参数估计值及其标准误。
应用实例
血吸虫的终宿主是广谱的,几乎所有哺乳类动物都可以是;而中间寄主钉螺则是唯一的。了解钉螺特性,快速获得钉螺的地理空间分布信息,并采取有效的灭螺措施是消灭血吸虫病的一项重要举措。本实例的钉螺样本数据来自某市2009年4月一个小区域钉螺分布调查的部分。具体调查方案是,在洲滩上纵深设线设点调查,每个样本点的尺寸大小是0.33米×0.33米予以制定,每个样点按照水线走向设定位置坐标,对样本点中的活钉螺予以计数,并记录与之相关的草丛密度,分为高密度(记为0)与低密度(记为1)两类。原始数据见表1。
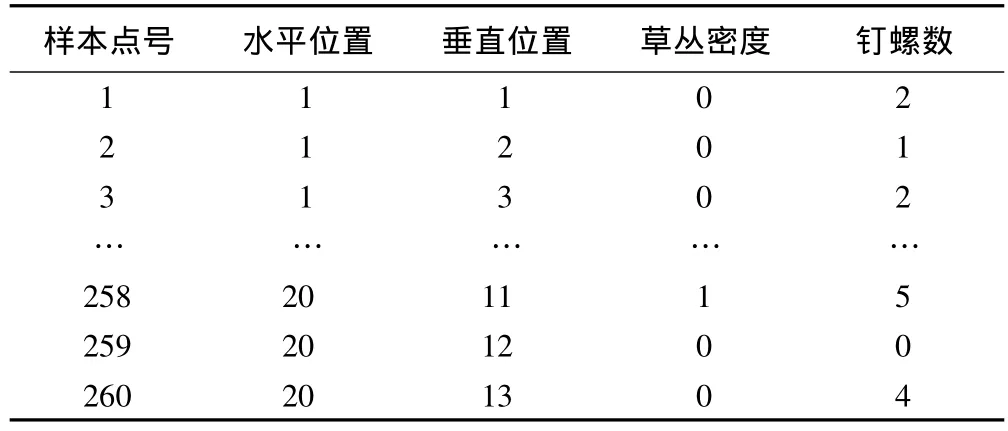
表1 钉螺调查数据
钉螺分布的均数为2.15,标准差为3.42,中位数为1,四分位数间距为2,可见钉螺的空间分布呈现出明显的正偏态分布,且可能存在离散过大趋势。Moran's I空间相依指数为0.188,P<0.0001,表明钉螺的空间分布具有一定的空间相关性。为了更直观地研究钉螺的空间相关性,对其作半方差图,见图1。
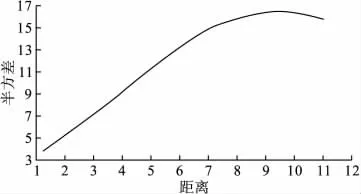
图1 原始钉螺分布的半方差图
从图1可以看出,原始钉螺空间分布具有一定的空间聚集性。块金值约为3.5,基台约为16,变程约为8,表明钉螺空间分布的变异较大,具有各向同性,并且存在着较长程的空间相关性。
为了更好地分析小范围钉螺分布的规律,拟合了常规的负二项回归〔11〕以及本文介绍的空间负二项回归,其参数估计与模型拟合见表2。
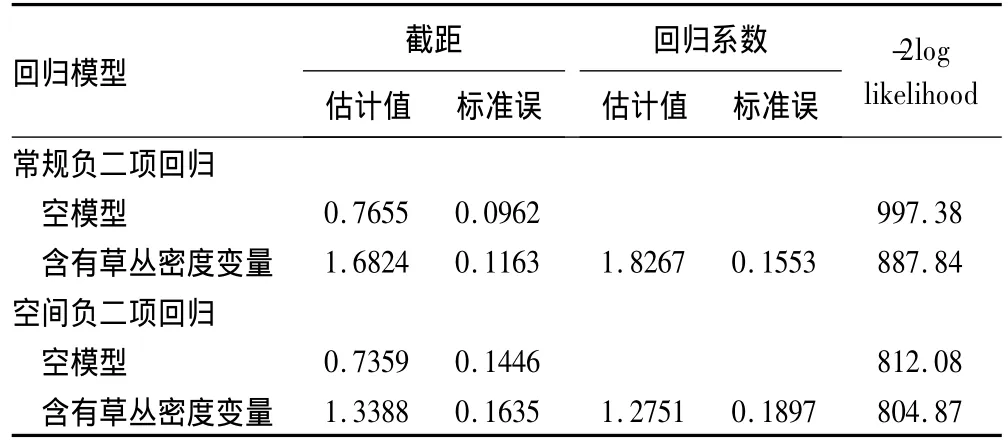
表2 常规负二项回归与空间负二项回归模型拟合与参数估计
由表2可以看出,无论拟合常规负二项回归,还是拟合空间负二项回归,各回归参数估计均具有统计学意义。这也就是说,无论是否考虑钉螺的空间相关性,草丛密度对钉螺分布均是具有一定的影响,提示其与钉螺的发生与发展具有较强的关联性。而从专业上讲,钉螺分布具有明显的空间聚集性,必须考虑其空间分布格局与聚集性特征。由表2可见,由于空间负二项回归考虑了钉螺的空间相关性,因而,从模型拟合的角度来看,相对于常规负二项回归而言,空间负二项回归的空模型与含有草丛密度变量模型的-2log likelihood统计量均有所下降。这表明无论是空模型,还是考虑草丛密度的模型,空间负二项回归模型拟合精度均有较明显的提高。由此可见,空间相关性对负二项回归模型存在着较强的影响。另外,从参数估计的角度来看,与常规负二项回归相比较,空间负二项回归模型截距与回归系数的估计值相对较小,而其标准误相对较大。这提示如果不考虑钉螺的空间相关性特征,那么,有可能会导致I型错误增大,使得负二项回归模型参数估计失效。
由于具有空间聚集性的解释变量纳入到回归模型,有可能会影响到反应变量空间相关性的分析结果,故而,必须在排除这部分解释变量的影响之后,重新审视反应变量的空间相关性。本实例中,从专业上讲,草丛也具有一定的空间聚集性,必须通过拟合含有草丛密度的空间负二项回归模型,排除草丛密度的影响,再对钉螺的空间相关性进行分析。拟合空间负二项回归模型后,其模型残差的 Moran's I空间相依指数为0.078,P<0.0001。与拟合空间负二项回归模型前的Moran's I空间相依指数相比较,该指数数值有所下降,这说明排除草丛密度的影响之后,钉螺的空间相关性有所降低。该统计量假设检验仍然具有统计学意义,这表明钉螺的空间分布仍然具有一定的空间相关性。见图2。
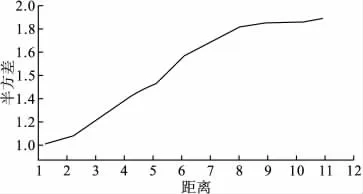
图2 拟合空间负二项回归模型排除草丛密度之后的钉螺分布的半方差图
与图1相比较,图2与图1存在着较强的相似性,半方差曲线走势大致相同,变程也约为8,只是块金值与基台值较小,分别为1.0和1.9。这表明拟合含有草丛密度的空间负二项回归模型,可以有效地降低钉螺空间分布的变异性,对钉螺的空间分布格局与规律没有产生较大影响,使得其空间相关性的基本趋势保持不变。
结 论
综上所述,空间负二项回归模型考虑了空间相关性的影响,是对常规的负二项回归模型的一种改进,可用于分析具有空间相关性的数据,能有效地降低空间相关性对回归系数估计的影响,更好地分析空间分布格局与规律。在实际应用中,如若数据存在着空间相关性时,必须将空间相关性纳入到统计分析考量之中,提高回归模型的拟合精度与效能。
1.空间相关性的处理
首先,对原始数据进行有关的空间统计描述,如,Moran's I空间相依指数,半方差图等,可以较为有效地发现数据可能存在的空间相关性的程度与模式进行初步分析。其次,在空间统计描述的基础上,结合资料的具体特点,拟合相应的空间回归模型,以提高回归模型的拟合精度,并保证回归系数估计的有效性。最后,在排除解释变量(可能具有空间聚集性的解释变量)的影响之后,通过残差来分析反应变量的空间聚集性与分布格局。
2.空间负二项回归模型的进一步改进
本文实例研究表明,空间负二项回归模型是一种可以用于分析具有空间相关性计数型反应变量的广义线性模型,可以处理因空间异质而导致的空间相关性问题。值得注意的是,该回归模型缺乏较好地处理因反应变量自相关性而导致的空间相关性问题。因此,空间负二项回归模型研究工作尚需从以下四个方面进行展开:(1)进一步探讨空间负二项回归模型的理论性质;(2)将反应变量的滞后变量作为解释变量纳入到回归模型之中;(3)逐步放松空间负二项回归的某些基本假定,扩展其适用范围;(4)对空间负二项回归模型进行统计模拟研究,探讨其统计效能,全面地了解空间负二项回归模型的特性。根据这些方向,将在以后的研究工作中对空间负二项回归进行更为系统的模型改进与理论研究。
1.Getis A,Mur J,Zoller GH.Spatial Econometrics and Spatial Statistics.New York,Palgrave Macmillan,2004.
2.Anselin L,Getis A.Spatial statistical analysis and geographic information systems.The annuals of Regional Science,1992,26:19-33.
3.Lawson BL.Statistical Methods in Spatial Epidemiology,2nd Edition.Chichester,UK:Wiley,2006.
4.苏德隆.苏德隆教授论文选集.天津:天津科学技术出版社,1995:97-101.
5.陈峰,杨树勤.疾病的复合分布模型研究-疾病的统计分布(一).中国卫生统计,1995,12(6):12-15.
6.赵安,鲍曙明.知识驱动的鄱阳湖区域钉螺分布预测模型研究初探.科学通讯,2007,52(22):2663-2670.
7.张志杰,彭文祥,ong Senghuat.广义负二项分布对钉螺分布的拟合.中国卫生统计,2008,25(1):2-6.
8.Geyer CJ.Markov chain Monte Carlo maximum likelihood.In Computing Science and Statistics:Proceedings of the 23rd Symposium on the Interface(ed.E.M.Keramidas).Interface Foundation of North America,Fairfax Station,VA.,1991:156-163.
9.Geyer CJ,Thompson EA.Constrained Monte Carlo maximum likelihood for dependent data(with Discussion).Journal of the Royal Statistical Society B,1992,54:657-699.
10.Hilbe MJ.Negative Binomial Regression.Cambridge University Press,Cambridge,U.K.,2010.

