宽级配泥沙分形特性及其输移规律试验研究
王洪虎,魏国远,王家生,闵凤阳
(长江科学院河流研究所武汉430010)
1 研究背景
泥沙在水流作用下的冲刷、悬浮、输移、沉积规律是河流动力学的重要理论基础,对分析河床演变趋势、河道治理具有重要意义[1],泥沙的级配分布是进行河床演变、冲淤计算、模型设计等问题研究中的基本参变量。由于宽级配泥沙群体组成不均匀程度较高,不同粒径的泥沙颗粒运动特性不同,且大颗粒泥沙对小颗粒泥沙存在隐蔽效应,影响着冲刷过程中细沙的输移。中值粒径及不均匀系数(多为2种特征粒径的组合)在描述颗粒级配时存在一定的局限性,级配曲线的描述相对繁琐且不能量化。
作为一种新的数学工具,分形理论很快被应用于定量描述颗粒的群体组成特性,并逐渐向河流泥沙研究的领域发展。赵辉[2]等以武水流域天然河道的53次降雨径流输沙过程实测资料为基础,分析了泥沙颗粒的级配特性及其分形规律。王协康[3]等针对过去床沙粗化试验中依据推移质输沙量确定粗化稳定的不足,利用分维测度提出了2种新的判别方法,即通过计算分析粗化层及推移质级配分维值稳定程度而加以识别。武生智[4]等用Weibul1分布模型分析研究沙粒粒径分布的规律。对于河流系统中的水流、泥沙运动与河床演变等具有自组织相似性(分形)的特性也已经得到了广大学者的认可[5-13],用分维数来描述泥沙粒径分布已显得更为简洁和科学。本文针对宽级配泥沙的分形特性,基于泥沙级配分形维数,通过多组次的天然沙水槽冲刷试验,研究宽级配泥沙粒径组成的分形特征,并分析不同流速、不同级配的床沙和推移质在不同水流条件下的粒度分维变化,以得出宽级配泥沙的分形特性及其输移规律。
2 试验概况
2.1 试验设备
试验设备由流量调节系统、水流循环系统、量测及其辅助设备组成。采用变频供水控制与计算机控制技术相结合,实现了变坡、流量、水位的全过程自动控制,尾门水位采用手动尾门和自动尾门双尾门方式控制,试验水槽布置如图1所示。

图1 水槽试验布置简图Fig.1 Scheme of the flume test arrangement
2.2 试验泥沙特性
水槽试验设计了3组(A,B,C)不连续宽级配床沙,1组连续宽级配床沙(D),试验设计床沙级配曲线见图2。试验沙采用天然黄沙与卵石配比而成,试验床沙粒径范围0.3~30 mm。试验沙粒径特征参数见表1,试验沙中值粒径范围为3.0 ~16.2 mm。

图2 试验设计床沙级配曲线Fig.2 Designed grading curve of bed material for the test

表1 水槽试验沙特征参数Table 1 Characteristic parameters of sediment for the flume test
2.3 试验组次及样品收集
试验根据天然沙粒径组成不同分为A,B,C,D 4个系列,又根据流量水位不同细分为A1,A2,A3,B1,B2,B3,B4,C1,C2,C3,D1,D2,D3 共 13 组试验,试验组次具体见表2。水槽进口铺长为3m卵石过渡段,卵石粒径20 mm,试验铺沙段长21 m,铺沙厚度6 cm。每组试验,分别在试验开始前和粗化稳定后取床沙样品,定义为初始床沙和末床沙。试验中按一定的时间间隔在槽尾收沙孔处收取推移质沙样,粗化完成后在距水槽尾部约5 m处对床沙进行取样,取样深度为4 cm,取样平面尺寸为20 cm×30 cm,将所取沙样烘干称重并进行级配分析。

表2 试验组次参数表Table 2 Parameters of different test groups
试验对比了不同流速及不同级配条件下泥沙样品的分维值变化,这些组次的对比克服了样品数量的不足,使得泥沙粒度分形的对比在范围上得到一定的丰富,同时多组次泥沙样品的分析也增加了分维值的可靠性。
3 分形分维计算
3.1 分维值计算方法
分形(Fractal)是用来描述那些表面看来杂乱无章、变幻莫测而实质上潜在有某种内在规律的几何图形或形状。自然界很多事物的现象在不同尺度上具有相同程度的不规则性和复杂性,即自相似性。将这种具有自相似性且有特征长度的图形称为分形。描述分形的一个重要参数是分形维数,简称分维[3]。
泥沙级配是对特定水沙条件及地理条件下形成的混合物的一种量度,其粒度组成是一种没有特征长度的结构图形,其分形是建立在一种统计分布上的,也就是说具有统计意义上的自相似性。根据分形理论[14],如果分形存在,则有关系式

式中:r为颗粒体积的立方根;N(r)表示粒径大于r的颗粒数目;D为分维数。对式(1)求导,可得

在常规粒度分析中,常用质量百分含量累积曲线来反映粒径级配,由颗粒粒径大小与频度的经验关系——Weibull分布,可得

式中:m(r)为直径小于r的颗粒累积质量;m为总质量;α为比例系数;b为幂指数。对此式求导则有

在假定颗粒密度不变的情况下,颗粒的质量与其直径的立方成正比,即频度的增量与质量的增量满足以下关系:

经过变量代换,得

所以粒度的分维数为 D=3-b。这样,只要在m(r)/m与r的双对数坐标图上找出直线段的斜率b值,就可以求得粒度的分维值,图3为B系列床沙的粒度分维曲线。
3.2 床沙分维值计算

图3 B系列床沙粒度分维曲线图Fig.3 Curves of granularity fractal dimensions of class B bed material
根据分形理论,以采得的床沙样品的级配曲线为数据源做直线拟合计算,即可获得相应的床沙分维值及其相关系数。本文分别对不同流速下的多组水流试验的初始床沙和末床沙进行了分维值计算,由于篇幅所限,仅列出B系列床沙粒度分维曲线,如图3所示,其中同系列不同组的初始床沙相同,计算得各组床沙的分维值,如表3所示。
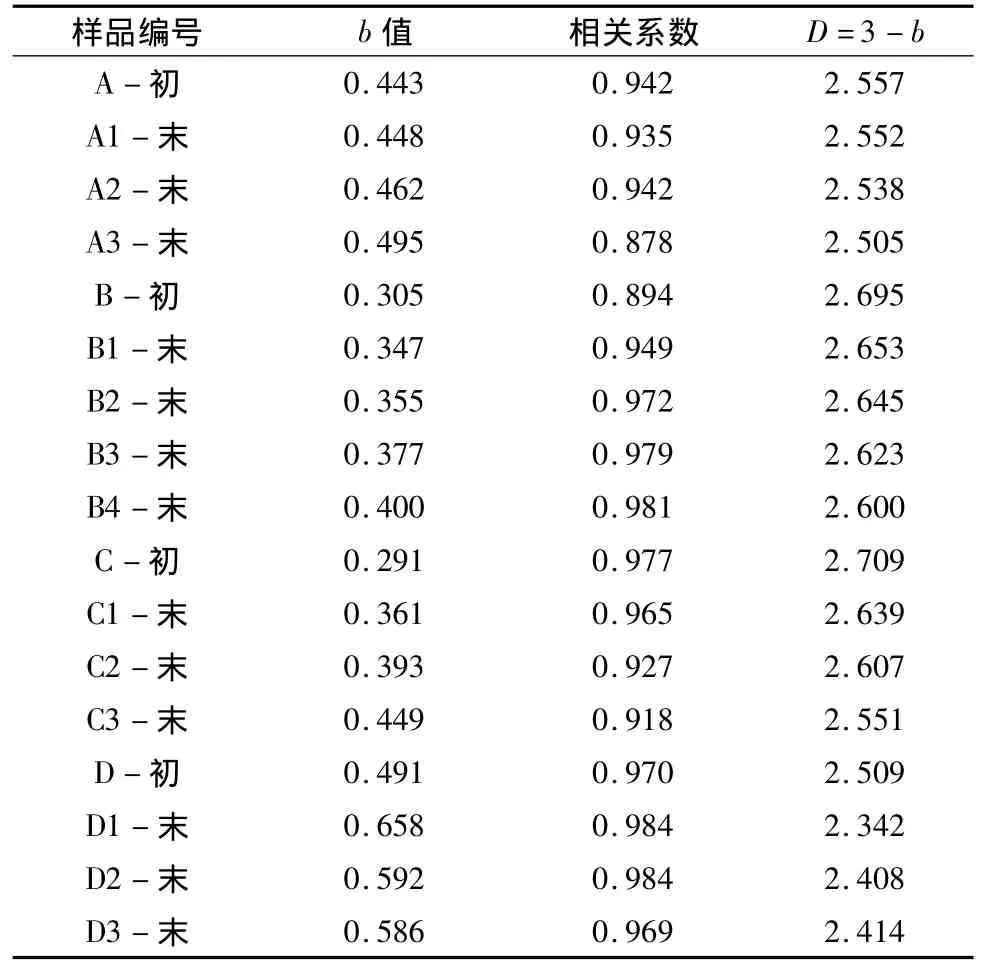
表3 床沙粒度分维表Table 3 Granularity fractal dimensions of bed materials
由表3可以看出,各组床沙分维值所对应相关系数都在0.87以上,多数在0.92以上,D系列则高达0.984。由此表明,床沙粒径分布具有统计自相似性,即分形特性。各系列床沙分维值范围为2.40~2.71,但差异明显:A,B,C系列非连续级配床沙分维值相对较大,而D系列连续级配床沙分维值相对较小。非连续级配A,B,C之间,当细沙所占比例较大时床沙分维值相对较大,细沙所占比例较小时床沙分维值相对较小,且所有初始床沙分维值大于末床沙分维值,这是由于床沙粗化后,细沙被水流冲走后占床沙的比例变小,大粒径卵砾石成为床沙主要组成部分,导致粒度分维曲线图“上扬”,b值增大,分维值减小。由此可推得,在非连续宽级配泥沙中,随着细沙所占比例的增大,分维值逐渐变大。
3.3 推移质分维值计算
根据分形理论,用相同方法进一步算出不同组次各推移质泥沙样品分维值及其所对应相关系数,列出了C和D系列推移质典型代表的粒度分维曲线,以显示连续级配与非连续级配样品粒度分维曲线的差异,如图4所示。将算得的各推移质分维值及其所对应相关系数进行统计,如表4所示。

图4 推移质典型样品粒度分维曲线图Fig.4 Curves of granularity fractal dimensions of typical bed load
由表4可以看出,各组次推移质样品粒度分维值所对应相关系数平均值在0.8以上,D1的平均值高达0.98,由此表明推移质粒度组成具有分形结构,即具有统计自相似性。A,B,C系列样品分维值所对应相关系数相对较小,而D系列样品分维值对应相关系数相对较大,这是由于A,B,C系列样品粒径组成为非连续型级配,级配曲线呈“躺椅型”,中间缺失的粒径形成“平台”,导致拟合时相关度偏低的原因。综合来看,各组次推移质样品分维值在1.6~2.9之间,但差异明显:连续型级配D系列样品分维值平均值相对较大,而非连续型级配A,B,C系列样品分维值平均值相对较小。

表4 推移质粒度分维表Table 4 Granularity fractal dimensions of bed load
4 分维值变化规律
4.1 床沙分维值与流速的关系
在对床沙和推移质分维值计算的基础之上,本文进一步探寻了床沙冲刷流速与冲刷达到粗化稳定后床沙分维值之间的内在联系。由于设计试验沙级配范围较宽,A,B,C 3组床沙缺失粒径范围较大,当水流速度较小时仅能起动细沙,无法观测到部分卵石的运动情况,为了能同时观察到细沙与卵石的起动输移情况,对细沙与卵石相互影响关系进行分析,故试验设计冲刷流速较大。根据泥沙起动流速公式计算得相应粒径卵石起动流速,结合试验实际情况设计试验流速范围为0.512~1.05 m/s,具体参见图5和表5。

图5 床沙粒度分维值与流速关系图Fig.5 Granularity fractal dimensions of bed material vs.flow velocity
由图5和表5可以看出,随着流速增大非连续级配A,B,C系列末床沙分维值逐渐变小,而连续级配D系列末床沙分维值逐渐变大。在2.2中已经说明了非连续宽级配床沙的变化规律是由于床沙粗化后细沙所占比例减小,使得粒度分维曲线尾部“上扬”导致的分维值变小。对于非连续宽级配床沙,随着流速的增大,粗化更加完全,所以粗化后细颗粒泥沙所占比例逐渐减小,使得分维值逐渐减小;对于连续宽级配床沙,随着流速的增大,细颗粒泥沙被冲走后,使得中间粒径段的比例增大,而大颗粒卵石比例并没有大的变化,使得粒度分维曲线中间段“翘起”,b值减小,分维值变大。

表5 床沙分维值与流速关系表Table 5 Granularity fractal dimensions of bed material vs.flow velocity
4.2 推移质分维值与中值粒径的关系
将计算出的各组推移质分维值与其所对应的中值粒径作成散点图,并拟合计算出两者之间的关系式,图6列出了几组典型推移质分维值与其所对应中值粒径的关系图。

图6 推移质粒度分维值与中值粒径关系图Fig.6 Granularity fractal dimensions of bed load vs.median diameter
由图6可以看出,推移质泥沙粒度分维值与中值粒径拟合的相关系数R高达0.977,二者存在显著的负相关性,即随着中值粒径的减小,分维值逐渐增大,虽然不同样品系列具体的关系式不同,但两者之间的负相关关系没有改变。由于数量有限,要得出具体的变化规律还有待进一步的深入研究,但是两者线性关系的存在,为将来分维值作为泥沙粒度的一个参数应用到泥沙领域的研究中提供了一定的依据。
5 结论
(1)床沙和推移质粒径组成具有明显的统计自相似性,即具有分形性结构的特征,但相关性的程度有所不同;连续型级配与非连续级配分维值具体变化规律不同。
(2)不同流速的床沙分维值存在明显差异,随着流速增大,非连续级配床沙粒度分维值逐渐变小,而连续级配床沙粒度分维值逐渐变大,且初始床沙粒度分维值比末床沙粒度分维值大。
(3)推移质粒度分维值与其对应的中值粒径之间存在显著的负相关性。
[1]王光谦.河流泥沙研究进展[J].泥沙研究,2007,(2):64-81.(WANG Guang-qian.Advances in River Sediment Research[J].Journal of Sediment Research,2007,(2):64 -81.(in Chinese))
[2]赵 辉,郭索彦,解明曙,等.湖南武水流域泥沙颗粒特性及分形规律研究[J].水土保持学报,2010,(3):45 -49.(ZHAO Hui,GUO Suo-yan,XIE Ming-shu,et al.Particle Sizes and Their Fractal Characteristics of Sediments from Wushui Watershed of Hunan Province[J].Journal of Soil and Water Conservation,2010,(3):45 -49.(in Chinese))
[3]王协康,方 铎,曹叔尤.宽级配卵石泥沙颗粒特性的分维值及其应用[J].长江科学院院报,1999,(5):9-12.(WANG Xie-kang,FANG Duo,CAO Shu-you.Fractal Dimension on Characteristics of Pebble Sediment with Wide Size Distribution and Application[J].Journal of Yangtze River Scientific Research Institute,1999,(5):9 -12.(in Chinese))
[4]武生智,魏春玲,马崇武,等.沙粒粗糙度和粒径分布的分形特性[J].兰州大学学报(自然科学版),1999,35(1):53 - 56.(WU Sheng-zhi,WEI Chun-ling,MA Chong-wu,et al.Fractal Analysis of the Roughness and Grading of Sands[J].Journal of Lanzhou University(Natural Science),1999,35(1):53 -56.(in Chinese))
[5]姚令侃,方 铎.非均匀沙自组织临界性及其应用研究[J].水利学报,1997,28(3):26 -32.(YAO Lingkan,FANG Duo.Study on the Self Organized Criticality of Non-uniform Sands and Its Application[J].Journal of Hydraulic Engineering,1997,28(3):26 - 32.(in Chinese))
[6]王协康,方 铎,姚令侃.非均匀沙床面粗糙度的分形特征[J].水利学报,1999,30(7):70 -74.(WANG Xie-kang,FANG Duo, YAO Ling-kan.The Fractal Characteristics of Riverbed Roughness with Non-uniform Sediment[J].Journal of Hydraulic Engineering,1999,30(7):70 -74.(in Chinese))
[7]王玲玲,金忠青.分形理论及其在紊流研究中的应用[J].河海大学学报,1997,25(1):1 -5.(WANG Ling-ling,JIN Zhong-qing.Fractal Theory and Its Application to Turbulence Study[J].Journal of Hohai University,1997,25(1):1 -5.(in Chinese))
[8]SHANG P J,SANTI K.Fractal Nature of Time Series in the Sediment Transport Phenomenon[J].Chaos,Solitons and Fractals,2005,26:997-1007.
[9]张之湘,惠仕兵,沈焕荣,等.宽级配卵石推移质输移随机过程的分维研究[J].泥沙研究,2000,(4):60-64.(ZHANG Zhi-xiang,HUI Shi-bing,SHEN Huanrong,et al.Fractal Study on the Stochastic Process of Bed Load Transport with a Wide Range Size Distribution[J].Journal of Sediment Research,2000,(4):60 -64.(in Chinese))
[10]周银军,陈 立,刘欣桐,等.河床表面分形特征及其分形维数计算方法研究[J].华东师范大学学报(自然科学版),2009,(3):170 - 178.(ZHOU Yin-jun,CHEN Li,LIU Xin-tong,et al.Study on Fractal Properties of a River Bed and the Calculation Method of Its Fractal Dimension[J].Journal of East China Normal University(Natural Science),2009,(3):170 - 178.(in Chinese))
[11]常福宣.分形理论在水文水资源研究中的应用[D].成都:四川大学,2001.(CHANG Fu-xuan.Applications of Fractal Theory in the Study of Hydrology and Water Resources[D].Chengdu:Sichuan University,2001.(in Chinese))
[12]汪富泉,李后强,艾南山,等.水流、泥沙运动及河床演变中的分形与自组织[J].大自然探索,1999,(3):55-61.(WANG Fu-quan,LI Hou-qiang,AI Nan-shan,et al.Fractals and Self-organizations of Motion of Flow and Sediment as well as Fluvial Processes[J].Exploration of Nature,1999,(3):55 -61.(in Chinese))
[13]钟 亮,许光祥.分形理论在紊流与泥沙研究中的应用现状[J].重庆交通大学学报(自然科学版),2008,27(5):806 - 811.(ZHONG Liang,XU Guang-xiang.Application Actuality of Fractal Theory in Turbulence and Sediment Studies[J].Journal of Chongqing Jiaotong University(Natural Science),2008,27(5):806 - 811.(in Chinese))
[14]柏春广,王 建.一种新的粒度指标:沉积物粒度分维值及其环境意义[J].沉积学报,2003,(2):234 -239.(BAI Chun-guang,WANG Jian.A New Grain-Size Index:Grain-Size Fractal Dimension of Sediment and Its Environmental Significance[J].Acta Sedimentologica Sinica,2003,(2):234 -239.(in Chinese))

