异质地层稳定渗流场随机多尺度有限元模拟研究

夏艳华

（安徽理工大学 土木学院，安徽 淮南232001）

1 引言

地下水渗流模拟是评估人类各种工程活动如地下水利用、石油开采、大坝建设等的重要手段［1］。由于地层形成经历了复杂的地质演变，地层的各种属性如渗透系数表现出多尺度异质性，这使得地下水渗流模拟变得极为复杂。如果运用标准的有限元计算，为了获取足够的精度，网格剖分需在细尺度上进行。这将带来如下两个方面的主要困难：一是由于网格剖分在细尺度上进行，将需要更多的计算资源，当研究区域较大时，以现有的物质基础，计算将无法完成；另一是需要知道整个研究区域上计算参数的变化。然而，事实上在岩土工程领域，人们只能获取局部的、有限的、稀疏的数据。

目前，研究随机渗流场的主要方法是基于概率理论的 Monte Carlo法、矩方程法和摄动法［2-5］，其中Monte Carlo法是最为有效的方法。最近有一种称之为广义多项式混沌的随机计算方法成为应用最为广泛的方法［6］，此法将随机场表达为输入随机变量的正交多项式，为了得到更好的收敛性，可以根据输入的随机变量选用不同类型的正交基。

但是这些随机计算方法没有考虑问题的多尺度性，当遇到在多尺度上不均匀的问题时，这些方法往往显得无能为力，因此需采用新的手段来模拟此类多尺度问题。目前研究者已提出了多种多尺度计算方法，在这些方法中，最常用的有多尺度有限元法（Ms-FEM）［7-8］、变分多尺度法（VMS）［9］和异质多尺度法（HMM）［10］。

HMM是解决多尺度微分方程的一般方法。其计算理念由两部分组成：一是宏观尺度上求解器的选取，即在宏观尺度上采用什么计算手段，目前通常采用有限元法；二是通过求解局部细观尺度问题估算所需的宏观诸如单元刚度矩阵、流通量等未知量。此计算方法能有效地解决具有高震荡系数的椭圆或双曲线问题。但是多尺度计算方法同样面临着需要详尽知道细观局部求解区间的计算参数如渗透系数的问题［11］。事实上，我们只能获取有限的、稀疏的、局部的数据，科学有效地描述这些数据往往需要借助随机模型。

综上所述，将随机计算方法与HMM结合是解决异质多尺度地层渗流问题的必经途径。因此提出结合有限元异质多尺度方法和基于广义多项式混沌的随机配点法的SHMFE法模拟异质随机多尺度渗透模型。在此方法中，将对数渗透系数Y＝lnKε在细尺度上用KL分解展开，然后采用稀疏格网配点法离散随机变量空间使随机模型变为确定性问题［12］，最后采用FEHM法求解此确定性问题。并通过计算实例对SHMFE有效性加以证明。

2 多尺度渗流模型

2.1 微观模型及均质化

2.1.1 微观模型

这里所研究的渗透模型其渗透系数取决于细尺度地层结构且在空间上是不均匀的。在研究区域D上，渗透模型在细尺度ε上的微分方程如下：

式中：kε为细尺度上渗透系数张量，假定该张量为正定对称张量；hε为细尺度上的水头；hD为Dirichlet边界∂ΓD上给定水头；gN为Neumann边界∂ΓN上给定流通量。

问题（1）可用标准的有限元进行求解，为了达到理想的精度，运用标准有限元求解时，需在模型最小尺度上进行网格划分。这意味着模拟需要大量的计算资源，当最小尺度ε远远小于研究区域尺度时，对当前的计算资源而言求解问题（1）是一个不可能完成的任务。这也是发展均质化理论的主要动机。

2.1.2 均质化模型

假定多尺度渗流模型是尺度分离的，根据均质化理论［13］问题（1）的解hε弱收敛于问题（2）的解h0：

式中：k0为均质化渗透系数张量，假定该张量为正定对称张量。

问题（2）的解h0称为均质化解，它不依赖于细尺度ε。通常均质化渗透系数张量k0是未知的，需要通过细尺度模型求解。

2.2 有限元异质多尺度法

均质化问题（2）可以通过有限元异质多尺度法进行求解。将问题（2）在宏观尺度上进行有限元近似，由于问题（2）的渗透系数k0未知，因此需通过微观尺度问题（1）上的已知数据来求解。具体实现是通过在宏观单元的每个积分点上求解微观模型来计算宏观单元的刚度矩阵。

问题（2）的弱解形式如下：

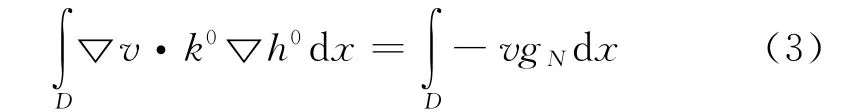
式（3）中的h0满足Dirichlet边界条件；v在Dirichlet边界上为0。

式（3）可以用传统的有限元法进行离散，假定TH为研究区域D 的网格剖分，K为离散域的有限元，问题（2）弱解形式有限元法进行离散的刚度矩阵通过如下的数值积分进行计算：

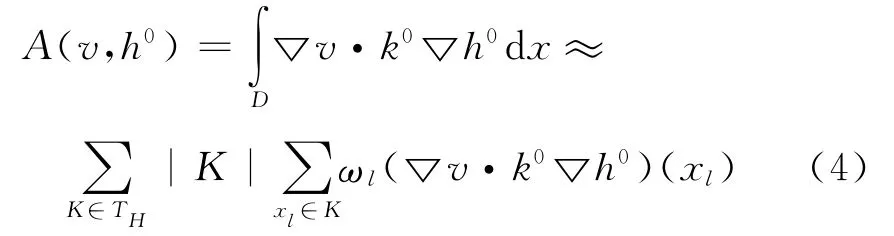
式中：｛xl｝为有限元K高斯积分点；｛ωl｝为有限元K积分权重；｜K｜为有限元K的体积。

由于k0未知，式（4）中（▽v·k0▽h0）（xl）是未知的，该未知量通过求解积分点处局部微观模型来近似得到，局部微观模型如下：

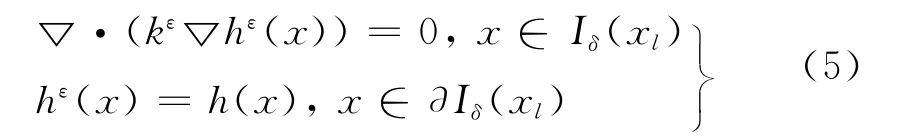
式中：Iδ（xl）为以积分点xl为中心边长为δ的立方体（三维）；水头h（x）为宏观水头h在积分点xl处泰勒展开的线性近似。

微观模型（5）的边界条件是Dirichlet边界条件，当然微观模型的边界条件也可以是其他形式的边界条件，如Neumann边界条件或周期边界条件等。

微观模型（5）也可以通过有限元求解，这样求解过程由两个嵌套的有限元求解器组成。在求解微观模型（5）的基础上，（▽v·k0▽h0）（xl）通过下式计算得到：

将式（6）代入式（4）得：

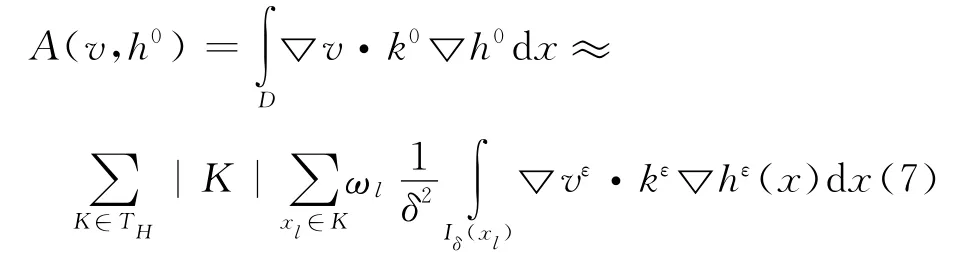
3 随机多尺度渗流模型

3.1 渗透系数随机场

地层渗透系数在空间上本质是异质的、多尺度的，由于不可能获取空间渗透系数完全的、详细的信息，渗透系数需要用随机理论来描述。一般认为渗透系数的对数Y（x）＝ln（kε）为一弱二阶平稳随机场，其均值在空间上为常数；协方差函数仅依赖于空间两点之间的相对距离［14-15］。为了使用数值方法求解随机渗流场问题，需对参数随机场（如渗透系数）进行离散化。这里通过Karhunen-Loμeve展开将参数随机场Y（x）离散化［16-17］，并近似截取有限项：

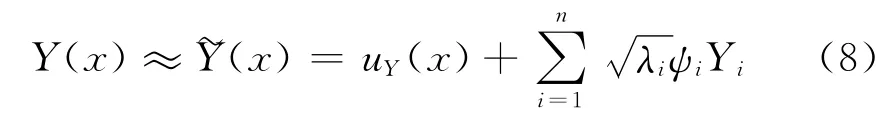
式中μY（x）为参数随机场Y（x）的均值；λi为随机场Y（x）协方差函数的特征值；ψi为与特征值相对应的正交特征函数，Yi为互不相关的随机变量，如果Yi是高斯随机变量，则他们是相互独立的。

3.2 随机多尺度渗流模型

如前所述，求解输入参数为随机变量的微分系统的传统数值计算方法主要包括Monte Carlo法、矩方程法、摄动法以及最近广泛使用的广义多项式混沌法。为了解决异质地层随机多尺度渗流问题，需在一个计算框架内同时考虑随机性和多尺度性，因此将广义多项式混沌法与有限元异质多尺度法结合起来是解决随机多尺度渗流问题的一个有效途径。

如果在计算中仅仅考虑渗透系数随机场（也可以考虑其他类型的随机场，如边界条件随机性、地层几何形态随机性等），考虑随机输入后的问题（1）变为如下随机微分方程：

式中：Ω为随机样本空间。

根据展开式 （8），输入随机参数共有n个互不相关的随机变量，令Y＝（Y1，Y2，…，Yn）为n维随机变量，Ψ为随机变量Y的样本空间，ρ为Y的联合分布密度，问题（9）的弱解形式为：

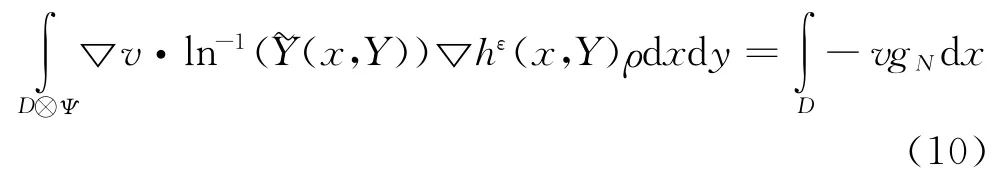
式中：y∈Ψ。

多种数值技术可以用来求解问题 （10）。在这些数值方法中，如同Monte Carlo方法一样，配点法将问题（10）的概率空间和物理空间实现解耦使之变成确定性问题。这样可以利用任何已有的数值方法来解决此确定性问题，可以有效利用已有的程序代码。

问题（10）是建立在细尺度上的，这将面临当细尺度远小于研究区域D时无法求解的问题，因此需借助多尺度计算方法。这里将问题（10）的物理空间用有限元异质多尺度法进行计算。假定物理空间是尺度分离的，类比（7），问题 （10）的刚度矩阵用下面的数值积分公式来近似：

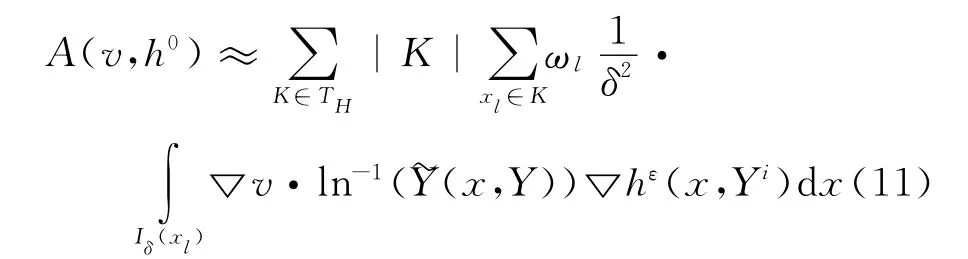
式中：Yi是n维随机变量的Y一个实现。

从（11）中可以得知，渗透系数随机场只需要在细尺度上局部区域进行展开，随机配点法的每一个实现实质上是用来求解宏观单元积分点处局部微观模型问题。由于渗透系数随机场只需要在微观局部展开，式（8）只需截取少数几项就可以达到所需精度。这一点对于随机配点法的计算极为重要，因为（8）中的n越大，随机变量空间的维数越高，所需的配置点就越多，这将需要大量的计算资源。因此SHMFE能有效地缓解当相关长度过小导致的概率空间维数过高的问题。SHMFE计算步骤概括如下：

（1）将渗透系数随机场按式（8）展开，得到n维随机变量Y，在此基础上通过配点法生成Nc个概率空间积分点；

（2）在概率空间每个积分点处通过有限元异质多尺度法求解确定性问题；

（3）按下面的公式计算随机渗流场的统计量平均值和方差：

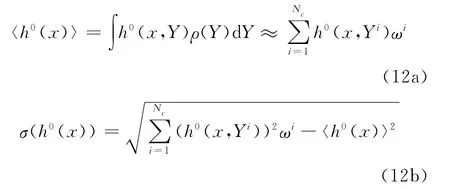
式中：ωi为积分权重。

4 算例

4.1 计算模型

算例选取的计算模型是一个具有不均匀多尺度渗透系数随机场的二维稳定渗流模型，用以说明SHMFE的计算过程及有效性。该计算模型来源于文献 ［17］，并对文献中的模型加了适当的修改。

计算模型的物理区域为（-1.5，0）×（-0.4，0.8）的矩形区域。模型物理区域左右两侧是定水头边界，总水头分别为hD＝1（x＝-1.5）和hD＝0（x＝0）。上下侧边为零流量边界。

渗透系数随机场按式（8）近似离散。如果在宏观尺度上进行展开，对于协方差函数是离散指数型的随机场，当相关长度为0.1时，由于特征值衰减缓慢，式（8）需要截取100项才能达到规定的精度（截取项的特征值之和占总特征值之和的90%）。如果采用SHMFE方法，由于只需在局部微观模型上展开，因而特征值衰减迅速，式（8）只需要截取少数几项就能达到规定的精度（假定微观模型的尺度与相关尺度相等，则只需4项即可）。因此，相对于随机SFEM方法，SHMFE能有效地克服概率空间维过高的问题。SHMFE的另一个优点是，计算仅需局部微观模型区域统计数据，这与工程实践一致，因为在工程中，能获取的只有局部数据，因此易获得相对可靠的微观区域统计模型。

算例仅为了说明SHMFE的有效性和可行性，而非实际工程，因此不具体考虑微观尺度ε、细尺度下代表体积单元（即局部微观模型尺度）以及统计模型相关尺度之间的关系。不失一般性，计算假定相关尺度各向同性且认为微观尺度ε、代表体积单元及相关尺度相等，并假定Y在局部微观模型区域按式（13）展开［18］：

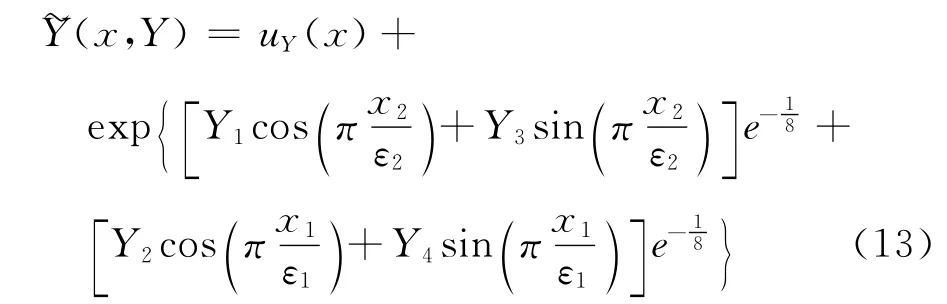
式中：ε为微观尺度。

在算例中，考虑相关长度取1，0.1，0.05和0.01等4种计算方案。在这4种计算方案中，假定（13）中的uY（x）只与宏观尺度有关，并令其等于sin（4＊x1＊x2）＋1。这4种方案均用SHMFE进行模拟。为了检验SHMFE可靠性，方案1除了采用SHMFE模拟外，还采用SFEM进行模拟，并将2种计算方法的结果进行对比。

4.2 计算结果

图1、图2是方案1（即相关长度η＝1）采用两种计算方法计算所得的水头随机场平均值和方差对比图，图1为平均值对比，图2为方差对比，图中虚线和实线分别为SFEM和SHMFE的计算结果。从图中可知，两种方法计算所得的结果是一致的，只在局部有细微的区别，这说明SHMFE方法可以获得全尺度的SFEM法计算结果。由于4种方案随机输入参数（参见（13）式）均值相同，所以4种方案计算所得水头随机场的均值均相同（见图1）。

图1 相关尺度为1时水头随机场平均值比较（虚线和实线分别为SFEM及SHMFE的计算结果）

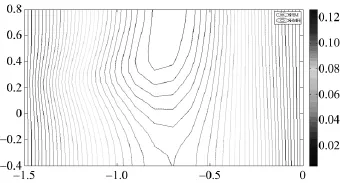
图2 相关尺度为1时水头随机场方差比较（虚线和实线分别为SFEM及SHMFE的计算结果）

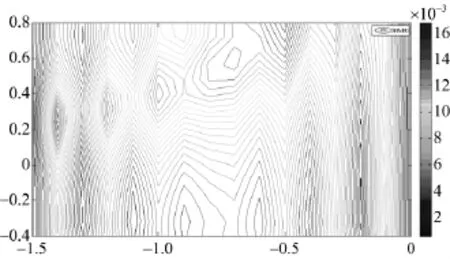
图3 相关尺度为0.1时水头随机场方差

图4 相关尺度为0.05时水头随机场方差

图2到图5是4种计算方案所得的水头随机场方差等值线图。计算结果表明，水头随机场摄动在研究的物理区域内是不均匀的，摄动主要集中在物理区域上侧，并且受相关尺度大小影响显著。当相关尺度与区域尺度同数量级时，水头随机场摄动集中在物理区域上侧中间，并从中间向两侧递减（见图2）；随着相关尺度减小（相关尺度比物理区域尺度小1个数量级），摄动集中区迅速向两侧扩散，出现多个集中区（见图3）；随着相关尺度进一步减小（相关尺度比物理区域尺度小2个数量级），在物理区域的上侧形成左右2个摄动集中区，且逐渐趋于稳定（见图4、图5），这说明相关尺度小于2个数量级后对计算结果基本无影响，事实上，此时（13）式中的随机部分在宏观尺度上可视为均质的，即满足尺度分离原则，水头随机场摄动变化是微观代表体积单元异质所导致。

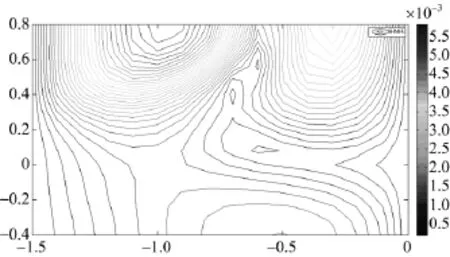
图5 相关尺度为0.01时水头随机场方差

从上述算例可知，SHMFE只需在宏观尺度上进行局部微观尺度计算就能很好地捕获到微观尺度异质性对宏观物理现象的影响，相对于SFEM而言具有更优的计算效率。

5 结语

（1）为了模拟异质多尺度地层稳定渗流场，提出了一种结合有限元异质多尺度法与随机配点法的随机异质多尺度有限元法。算例表明，相对于SFEM而言，SHMFE能用更少的计算资源有效地捕获异质渗透系数随机场对渗流随机场的影响。该方法结合了HMM和SFEM的优点，同时能有效地克服SFEM概率空间维过高的问题；另一方面，计算只需局部微观模型数据，这与实际工程获得的数据结果一致。

（2）本文没有讨论微观尺度ε、代表体积单元和相关尺度的关系对计算结果的影响，也没有讨论尺度分离问题对计算结果的影响，这些问题需进一步研究。

［1］Eaton TT.On the importance of geological heterogeneity for flow simulation［J］.Sedimentary Geology，2006，184（3-4）：187-201.

［2］P.E.Kloeden，E.Platen.Numerical Solution of Stochastic Differential Equations ［M］. Berlin： Springer-Verlag，1999.

［3］I.Karatzas，S.E.Shreve.Brownian Motion and Stochastic Calculus［M］.New York：Springer-Verlag，1988.

［4］G.S.Fishman.Monte Carlo：Concepts，algorithms，and applications［M］.New York：Springer-Verlag，1996.

［5］B.Oksendal.Stochastic Differential Equations：An Introduction with Applications ［M］. Berlin： Springer-Verlag，1998

［6］D.Xiu，G.E.Karniadakis.The Wiener-Askey polynomial chaos for stochastic differential equations［J］.SIAM J.Sci.Comput.，2002，24（2）：619-644

［7］Y.Efendiev，T.Y.Hou.Multiscale Finite Element：Theory and Applications［M］.New York：Springer，2009.

［8］T.Y.Hou，X.-H.Wu，Z.Cai.Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients［J］.Mathematics of Computation 1999，68（227）：913-943

［9］T.J.R.Hughes，G.R.Feijo，L.Mazzei，J.-B.Quincy.The variational multiscale method—aparadigm for computational mechanics［J］.Computer Methods in Applied Mechanics and Engineering，1998，166（1-2）：3-24.

［10］E.Weinan，B.Engquist，X.Li，W.Ren，E.Vanden-Eijnden.Heterogeneous multiscale methods：a review［J］.Communications in Computational Physics，2007，2（3）：367-450.

［11］A.Abdulle，A.Nonnenmacher.A short and versatile finite element multiscale code for homogenization problems［J］.Computer Methods in Applied Mechanics and Engineering，2009，198（37-40）：2839-2859.

［12］F.Nobile，R.Tempone，C.G.Webster.A sparse grid stochastic collocation method for partial differential equations with random input data［J］.SIAM Journal on Numerical Analysis，2008，46（5）：2309-2345.

［13］D.Cioranescu，P.Donato.An Introduction to Homogenization［M］.Oxford：Oxford University Press，1999.

［14］李少龙，张家发.非均质土体中渗流场的非平稳随机模拟［J］.长江科学院院报，2009，10：49-53

［15］D.Xiu，J.S.Hesthaven.High-order collocation methods for differential equations with random inputs［J］.SIAM Journal on Scientific Computing，2005，27（3）：1118-1139.

［16］R.Ghanem，P.D.Spanos，Stochastic Finite Elements：A Spectral Approach ［M］. New York：Springer-Verlag，1991.

［17］Z.Chen，T.Y.Hou，A mixed multiscale finite element method for elliptic problems with oscillating coefficients［J］.Mathematics of Computation，2003，72（242）：541-576.