基于遗传算法的电动助力转向系统的μ鲁棒控制*

熊 行

(湖南大学机械与运载工程学院，湖南长沙410082)

基于遗传算法的电动助力转向系统的μ鲁棒控制*

熊 行

(湖南大学机械与运载工程学院，湖南长沙410082)

电动助力转向系统是一个多输入输出非线性系统。本文首先对控制系统做动力学分析，建立动力学模型，在此基础上对系统设计一种基于遗传算法的μ综合方法，借用μ综合问题的常用D－K交替迭代算法，将定标矩阵D和控制器K作为遗传算法的解空间，以最大奇异值作为目标函数来获得最优控制器K，从而获得μ值判定设计控制器对系统有好的性能以及稳定性。

电动助力转向系统;遗传算法;μ综合设计;鲁棒控制

汽车作为全球最主要的交通工具，汽车工业不断的发展，且必将长期繁荣发展。目前汽车电子已成为汽车技术的重要组成部分，并且实现了许多部件的汽车电子化。汽车转向系统在经历机械转向和液压转向两个发展阶段后，也将被电动助力转向系统所取代。

另一方面，由于汽车、安全上的要求十分严格，所以电动助力转向的稳定性和可靠 性是产业化发展的关键因素。控制系统是电动助力转向系统的核心组成部分，本文在控制层面寻求新的控制方法，改善控制方法，通过综合遗传算法和μ综合控制的方法来设计EPS的控制系统，设计基于遗传算法的EPS的μ综合鲁棒控制方法。

通过matlab/simulink对电动助力转向系统进行仿真，并且通过比较分析上述控制方法获得的仿真结果。

一、电动助力转向模型的建立

对转向盘和转向柱进行受力分析［1］，得到运动方程:

对齿轮齿条进行受力分析，得到齿轮齿条模型:

系统采用永磁式直流电动机，有如下关系:

电动机产生电磁转矩:

减速系统机机械部分受力分析，可得到:

分析电动助力转向系统模型，遵循建立数学模型的基本原则，适当简化控制系统，使系统结构尽可能清晰，系统内互相耦合尽可能少，并考虑部分可能影响系统的误差因素并且建立数学模型。如图1所示，简化后的系统包括:转向盘，转向柱，助力电机，减速系统，齿轮齿条五个主要部分。根据系统的结构建立各个部分的运动微分方程，从而选取合理的输入输出项，建立整个系统的模型。

公式中参数如下所示:

Td为转向盘的输入扭矩;Tm为电动机理论输出扭矩;θc为转向柱转角;θm为助力电机转角;Xr为齿条位移;Jc为转向柱的转动惯量;Kc为转向柱的刚度;Bc为转向柱的阻尼;M为齿条质量;Br为齿条阻尼;Kr为齿条当量刚度;Km为电动机扭转刚度;Jm为电动机转动惯量;Bm为电动机阻尼系数;G为电动机到转向柱的减速比;rp为转向小齿轮节圆半径;Bc为转向柱粘性阻尼系数;fc(θc，˙θc)为转向柱及连接副的摩擦力矩;Mr为齿条等效质量;Kt为齿条当量刚度;fr(xr，)为齿条上非线性摩擦力;Fr为路况变化对系统的干扰力;Ka为电动机的转矩系数;U为电动机的电压;L为电感;R为电枢电阻;Kb为反电动势常数;I为电流;t为时间。

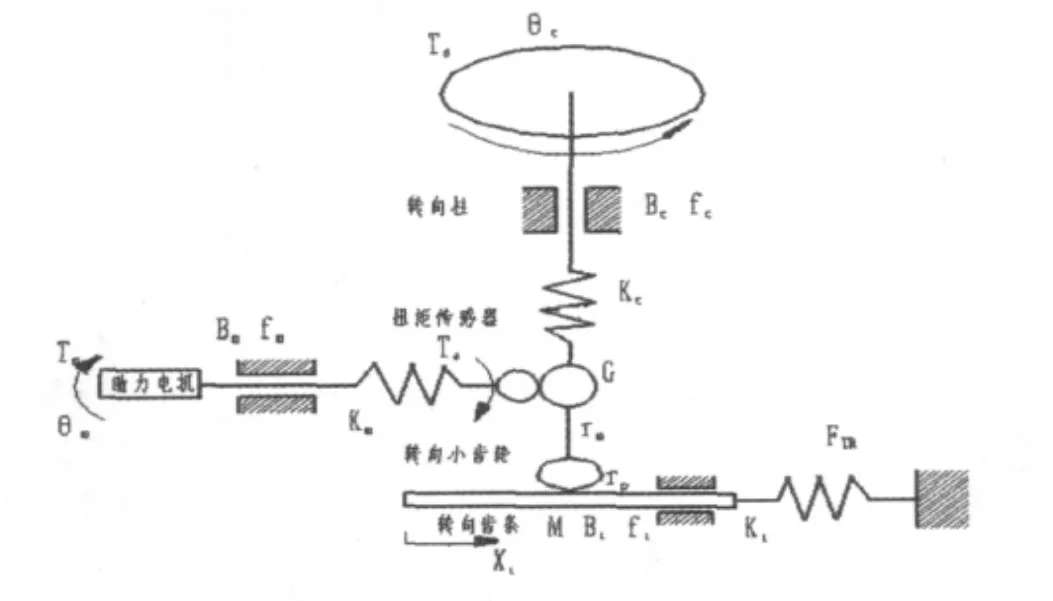
图1

二、状态方程的建立

由上述(1)－(5)建立系统状态方程模块，其中状态变量为:

输入量为:U= [TU F]T，

系统的状态方程和输出方程式为:

为了减少系统建模的保守型，在进行传感器测量时，系统性能不可避免的会受到传感器噪声的影响，为此设定权函数:WTc=Wθc=W˙θm=0.01。并且分离系统高频未建模摄动。

三、基于遗传算法的μ综合控制

对于μ综合问题的描述一般如图2所示。

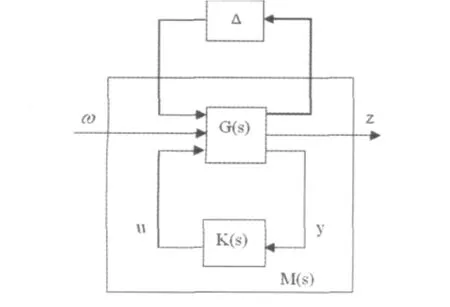
图2

其中G为被控制对象，K为控制器，M=Fl(G，K)。μ综合问题即为寻找一个控制器K*，使得M*满足这样就可以通过对μ的计算来解决μ综合问题。

定义:对于任意矩阵 A∈ Cm×n，可以表达为:A =U∑V*。其中U∈Cm×n，V∈Cm×n是单模矩阵，即有 UU*=I，VV*=I，∑∈Rm×n的非对角元素为0，对角元素σi非零且有p=min(m，n) 个，假定为 σ1≥ σ2≥ … ≥ σp，则 σ1，σ2，…，σp称为矩阵的奇异值，其中σ1为最大奇异值。对于实数矩阵A∈Rm×n，U和 V是实正交矩阵。矩阵 A的最大奇异值有:

定义如下两个Cm×n的子集的集合。

利用μ的定义很难对μ进行求解，目前最常见的方法是通过一组上下界函数来逼近μ值。

定理1:对于任意D∈D和U∈U，有:μ(MU)=μ(UM)=μ(M)=μ(DMD－1)成立。由定理一可得一个关于μ(M)的一个比较接近的上下界，即μ 上界为最大奇异值。

定理2:最大奇异值最小化问题是凸优化问题。

定理2提供一种利用μ的上界近似求解μ的思路。所以μ 的计算一般指上界函数

简单描述D－K交替迭代算法的具体步骤:首先选择一个定标矩阵D(s)，使D(s)和D(s)－1稳定，并且最小化广义系统，然后使用H∞设计方法，寻找一个控制器K。对于控制器K(s)，在每个频率点上求解最优的D(s)，用稳定、最小相位，可逆的传递函数拟合D(s)阵。反复迭代，直到μ［Fl(G，K)］满足一定要求为止。

在D－K交替迭代算法中，用定标矩阵D和控制器K反复迭代，两步都是凸优化问题，但是D－K交替迭代寻优不具备联合凸性［2］。所以这种算法不能保证最终获得的控制器是最优控制器。而在μ－K迭代中，用μ替代D－K迭代中的D，同样不存在全局最优性，而且需要较大的计算量。

遗传算法是一种有效的全局优化搜索算法［3］，特别适于处理传统寻优方法难以解决的复杂非线性寻优问题［4］。通过选择多个满足D子集的定标矩阵D，然后利用H∞设计方法寻找相应的满足最小化广义系统的H∞范数的控制器K，最后通过对定标矩阵D和控制器K进行遗传操作得到控制器K*。

遗传算法的处理:编码:将定标矩阵D主对角线各项和控制器 K 中 的 各 项 直 接 编 码，组 成 个 体 P。P:设定初始群体:选择多个满足Dj(j=1，2，…，N)，然后利用H∞设计方法寻找相应的控制器Kj(j=1，2，…，N)，这样就得到 N 个个体 Pj(j=1，2，…，N)，将这 N 个个体组成初始群体。

定义适应度函数的目标函数为:φ =σmax［DFl(G，K)D－1］，定义适应度函数为为交叉概率为变异概率。其中M为较大正数保证适应度值总是正的。

设计遗传操作:(1)选择:排序选择+最佳个体保存法;(2)非一致交叉，个体P由定标矩阵D和控制器K两部分组成，因此需要对两部分分别进行非一致交叉。设进行交叉的两父代个体为:X1D，X1K，X2D，X2K:

其中:rD，rK∈［0，1］，每次交叉时的取值都不同。

(3)变步长变异:分别对个体P的两部分进行变步长变异。变异步长为:

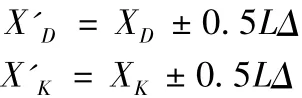
其中:XD，XK和X'D，X'K分别为变异前和变异后的个体。

(4)遗传算法的迭代终止条件:设置最大进化代数G作为迭代终止的另一个条件。

(5)设计方法如图3所示。

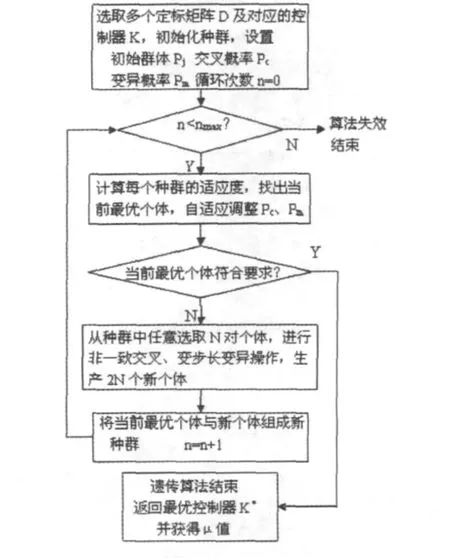
图3

四、仿真结果及分析

设定系统参数有:群体规模N=12;最大进化代数G1=100;定常系数 α 为0.02;β 为0.3;定常系数 k1为0.85;k2为0.01;Jc=0.0012kg.m2;Kc=90Nm/rad;Bc=0.261N.m.s/rad;M=32kg;Br=650.5N.m.s/rad;Km=125Nm/rad;Jm=0.00047kg.m2;rp=0.0078m;Bm=0.00334N.m.s/rad;G=16.5;Kt=91061N/m;L=0.0015H;R=0.1Ω;Kw=0.02v.s/rad;Ke=0.02v.s/rad。

通过全局寻优的μ综合的遗传算法，利用Matlab工具箱进行仿真，得到μ=0.7560。结构奇异值 μ的曲线如图4所示。

图4

由上诉仿真结果可以表明，基于遗传算法的μ综合问题与传统的交替迭代算法相比，具有简便性，并且能达到全局最优解。由图可知μmax＜1，所以可知系统在高低频段可以具备良好的鲁棒性。

如图5所示，为目标转矩对助力转矩阶跃响应曲线图，比较之后我们可以看出基于遗传算法的μ鲁棒控制，具有超调量小，反应速度快，并且能够迅速稳定的特点，从而使得系统具有更好的动态性能和稳定性能。

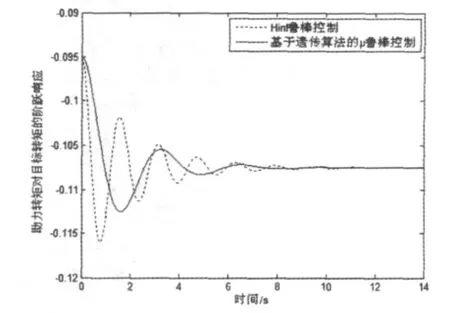
图5

图6是扭杆转矩对助力电机电压扰动阶跃响应，从图中可以看出，基于遗传算法的μ鲁棒控制具备响应速度快，超调量小，且干扰小的优点。

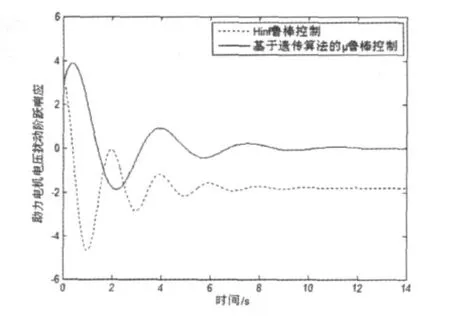
图6

五、结论

在本文中，建立了电动助力转向系统，并对其设计了基于遗传算法的μ鲁棒控制的方法，系统仿真结果表明，基于遗传算法的μ鲁棒控制具备良好的鲁棒性能。通过基于遗传算法的μ鲁棒控制与Hinf鲁棒控制的比较，可以看出μ鲁棒控制具备超调量小，干扰小，响应速度快的优点。

［1］余志生.汽车理论(第3版)［M］.北京:机械正业出版社，2000.

［2］Mu －Analysis and Synthesis Toolbox.The Mathworks，Inc.

［3］潘伟.基于遗传算法的鲁棒控制问题研究［D］.沈阳:东北大学，2006.

［4］王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安:西安交通大学出版社，2000.

2012－03－02

熊行(1985－)，男，湖南长沙人，硕士研究生。