一种改进的最小属性约简算法＊

薛胜军 郭 强

（武汉理工大学计算机科学与技术学院1） 武汉 430063）

（南京信息工程大学计算机与软件学院2） 南京 210044）

粗糙集理论是一种新型的处理模糊性和不确定性问题的数学工具，经过将近30 a的发展，该理论已广泛应用于故障检测、数据挖掘、模式识别、知识发现等领域．属性约简是粗糙集理论中的一个核心内容，目前有很多研究都是针对属性约简方面的．求解属性约简的算法可以划分为如下几类：（1）基于正区域的求解算法，有时在求解的过程中会结合属性的重要性、互信息等；（2）基于差别矩阵的求解算法；（3）基于智能计算的求解方法，如基于遗传算法和神经网络．随着问题规模的增大，基于差别矩阵求解算法的缺陷会愈加凸显．有时在利用正区域或差别矩阵求解时，常结合属性的重要性［1］、互信息［2］、属性出现的频率［3］等，使得算法更加高效．本文通过实例指出文献［4］中的不足并加以改进，结合了基于等价类压缩的思想和基于核增量求解的思想提出了一种新的求解最小约简的方法，最后通过实例验证算法的有效性．

1 粗糙集的相关概念

设S＝（U，R，V，F）为一信息系统．式中：U＝（X1，X2，…，Xn）为论域（universe）；R 为属性集合；V为属性值集合；F为U×R→V 的映射，它为U中各对象的属性指定惟一值．若R＝C∪D，C∩D＝∅，C称为条件属性集；D称为决策属性集，则该信息系统称为决策表．

定义1 设S＝（U，R，V，F），对于每个属性子集P⊆R，定义属性P的不可区分关系IND（P）＝｛（x，y）∈U2｜∀r∈P，f（x，r）＝f（y，r）｝，如果（x，y）∈IND（P），则称x与y 是P 不可区分的．不可区分关系也可称为等价关系．IND（P）是U 的一个划分，记为U／P，U／P中的任意元素［x］P＝｛y｜∀a∈P，f（x，a）＝f（y，a）｝称为等价类．

定义2 设S＝（U，R，V，F），对于每个子集X⊆U和一个等价关系P⊆R，定义两个子集：＝｛Y∈U／R｜Y⊆X｝，X＝｛Y∈U／R｜Y∩X≠∅｝．分别称它们为X的P下近似集和P上近似集．

定义4 设S＝（U，R，V，F），R＝C∪D，如果POSP（D）＝POSC（D）且对于∀r∈P，都有POSP（D）≠POSC－｛r｝（D），则称P 是S 的一个属性约简．S的所有属性约简的并集记为red（S）．red（S）中属性数目最少的约简称为S的最小属性约简．

定义5 决策表S的所有属性约简的交集为属性核，即core（S）＝∩red（S）．

定义6 如果有相同条件属性的数据同时其决策属性的值也相等，则称该决策表为相容决策表，如果它们的分类不相同，则称为不相容决策表．

定义7［5］决策表S＝（U，R，V，F）的差别矩阵M（S）是一个n×n的矩阵，n＝｜U｜，其第i行第j列的元素为Cij＝｛a∈C｜f（ui，a）＝f（uj，a），（ui，uj）∉IND（D）且ui，uj中至少有一个属于POSC（D）｝；否则Cij＝∅．

推论1 在基于定义7的条件下，core（S）＝｛a∈c｜Cij＝｛a｝｝．

2 基于U／｛a｝的最小属性约简算法

该方法的思想在于先用单个条件属性a对论域U进行划分，获得若干子决策表，然后对各子决策表求解，整合各子决策表中的基数最小的约简，将这些约简合并到集合Gm中，若p∈Gm，POSp（D）＝POSC（D），则p为所求，否则p∪｛a｝为所求．该方法具有如下性质．

定义8［6］决策表Si＝（Ui，r－｛a｝，V，F），P⊆A，U／P＝｛X1，X2，…，Xn｝，知识P 的 划分粒度E（P）定义为E（P）＝ ｜Xi｜

性质1 决策表S＝（U，R，V，F），P⊆A，U／P＝｛X1，X2，…，Xn｝，则1≤｜U｜／n≤E（P）≤｜U｜．即划分粒度越小，分类能力越强．当n＝｜U｜时划分粒度最强．

定义9 决策表S＝（U，R，V，F），R＝C∪D，a∈C，n＝｜Va｜，U／a＝｛U1，U2，…，Un｝，则第i个等价类构成原决策表S的第i个子决策表（1≤i≤n），记为Si＝（Ui，R－｛a｝，V，F）．差别矩阵为M（Si），差别集为 AS（i），约简集为red（Si），G＝｛Ra｜Ra＝∪Ri，Ri∈red（Si）｝，H＝｛Ra∪｛a｝｜Ra∈G｝．设G中元素最小基数为m，Gm＝｛R｜R∈G，｜R｜＝m｝．

定理1 若G＝∅，则POS｛a｝（D）＝POSC（D）．

性质2 Ui∈IND（D）当且仅当red（Si）＝∅．

定理2［7］H∪G中必存在原系统的最小约简．

定理3 任取RS∈red（S），则在每一个子系统Si中都存在P∈red（Si）满足P⊆RS．

引理 ∪core（Si）⊆core（S），其中1≤i≤n．

证明 由定理3即可得到．

文献［4］中的方法没有考虑如果Gm中的元素全为核属性时的情况．因为核属性必属于最小约简，但是根据文献［10］的思想，只能随机的选取其中一个核属性，必会漏选其他的核属性，所得的结果就不是正确的了．另外，文献［4］中的方法是对整个论域元素依次进行计算，这就会出现重复计算的现象，增加了算法的复杂度，降低了效率．

3 基于等价类的决策表压缩方法

定义10［8］在 决策表 S ＝（U，C，D，V，F）中，记U／C＝｛［u′1］C，［］C…［u′m］C｝，U′＝｛u′1，u′2，…，u′m｝，POSC（D）＝］C∪ ［u′i2］C∪ … ∪］C，其中∀∈U′且｜［］C／D｜＝1（s＝1，2，…，t）；记U′pos＝…｝，U′neg＝ U′－U′pos，称S′＝（U′，C，D，V，f）为简化的决策表．

定理3 在决策表S＝（U，C，D，V，F）中，S′＝（U′，C，D，V，f）为其简化的决策表．若∀B⊆C有（D）＝且∀b∈B 均有（D）≠P（D），则B 是C 相对于D 的属性约简．

推论2 在不涉及决策属性计算的情况下，简化后的决策表的分类能力不变．

证明 在压缩后的决策表中，各等价类之间的计算仍然不变，只是减少了差别矩阵中非空元素的重复计算，即各等价类之间只计算一次．此时，用于计算结果的分辨信息并未减少．又由定理3可知，压缩后的决策表的约简满足原决策表，从而推论得证．

文献［8］提供了一种快速的求解等价类的方法，该方法在目前是最快的，算法的具体内容可参考文献［8］．通过该方法的计算，可以得到Upos和Uneg，将它们压缩后便可得到新的论域＝∪．以文献［4］中的例子为为例，经计算，可得等价类｛1，5｝，｛2，8｝，｛3｝，｛4｝，｛6｝，｛7｝．具体步骤如下．

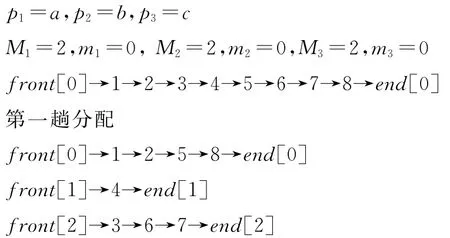
第一趟收集

front［0］→1→2→5→8→4→3→6→7→end［0］

第二趟分配

front［0］→1→2→4→5→7→8→end［0］

front［1］→3→end［1］

front［2］→6→end［2］

第二趟收集

front［0］→1→2→4→5→7→8→3→6→end［0］

第三趟分配

front［0］→1→5→end［0］

front［1］→2→7→8→end［1］

front∪［2］→3→4→6→end［2］

第三趟收集

front［0］→1→5→2→7→8→3→4→6→end［0］

其中：｛1，5｝，｛2，8｝是不相容的，｛3｝，｛4｝，｛6｝，｛7｝是相容的，可以用｛1｝或者｛5｝来代替｛1，5｝，｛2｝或者｛8｝来代替｛2，8｝．则压缩后可得U′pos＝｛3，4，6，7｝，U′neg＝｛1，2｝，U′＝U′pos∪U′neg．在构成的新的差别矩阵时，减少了元素2，8分别和元素3，4，6，7之间的计算．在数据量较大的运算中，该方法的优势会更加明显．

4 基于核的改进算法

本算法对文献［4］提出的基于U／｛a｝的最小属性约简算法进行了改进，具体步骤如下．

步骤1 按公式计算出最小划分粒度｛a｝，若POS｛a｝（D）＝POSC（D），则｛a｝为最小约简，退出，否则转步骤2．

步骤2 对论域进行压缩，求出S′＝｛U′，R，V，F｝．

步骤3 用粒度最小的元素对论域进行划分，采用文献［5］中的方法，对各个子系统进行计算，求出约简集red（Si）．

步骤4 将AS（i）中的单元素存入core中，保持core中各元素互不相同，并在red（Si）中删除所有由单元素所组成的约简．

步骤5 如果POScore（D）＝POSC（D），则core为最小约简，退出，否则转步骤6．

步骤6 如果POScore∪｛a｝（D）＝POSC（D），则core∪｛a｝为最小约简退出，否则转步骤7．

步骤 7 求 G＝ ｛Ra｜Ra＝ ∪Ri，Ri∈red（Si）｝，计算Gm＝｛R｜R∈G，｜R｜＝m｝．

步骤8 如果存在Gm中一元素p，使POSp∪core（D）＝POSC（D），则p∪core为最小约简，退出，否则，任取p∈Gm，p∪core∪｛a｝为所求，退出．

该算法能在Gm中的元素为核属性的情况下求的最小约简．

证明 假设步骤1得到的不是最小约简，则必存在元素数目小于1的约简，此时只有空集，不符合要求，则｛a｝为最小约简，步骤1得证．由推论2知步骤2不会影响结果的计算．依据定义5，若POScore（D）＝POSC（D），则core为最小约简，步骤5得证．若POScore∪｛a｝（D）＝POSC（D），则core∪｛a｝是最小约简．假设其不是，则必存在元素数目更小的约简，因core（S）＝∩red（S），所以该约简至少包含core且包含元素数目不小于｜core｜，又POScore（D）≠POSC（D），所 以 假 设 不 成 立，则core∪｛a｝为最小约简，步骤6得证．因约简必包含core，又p中包含的元素最少，则p∪core为最小约简，否则，若 POSp∪core∪｛a｝（D）＝POSC（D），此时正好满足文献［4］中算法求解的条件，由文献［4］中证明可得p∪core∪｛a｝为最小约简，步骤8得证．

该算法考虑了各核属性，解决了文献［4］中基于U／｛a｝的最小属性约简算法的不足．步骤2的复杂度为O（｜C｜｜U｜），在实际问题中｜C｜｜U｜＜｜U｜2，又原算法的时间复杂度为O（K｜U1｜2＋K｜U2｜2＋…＋K｜Un｜2），K 为关于｜U｜与｜R｜的多项式或指数级式子，则改进后的算法的时间复杂度为 max（｜C｜｜U｜，K｜U1｜2＋K｜U2｜2＋…＋K｜Un｜2），随着数据量的增大，时间复杂度会趋向于O（K｜U1｜2＋ K｜U2｜2＋…＋ K｜Un｜2），由于对原决策表进行压缩，所以新的算法的空间复杂度会降低，这种优势在大数据量的计算中会很明显．

5 实例分析

分别采用文献［4］的算法和本文的算法对表1进行计算，求该决策表的最小属性约简．

表1 决策表

E（｛a｝）＝62／12，E（｛b｝）＝50／12，E（｛c｝）＝72／12，E（｛d｝）＝102／12，故用属性b对论域进行划分．对论域进行压缩，压缩后得＝｛X1，X2，X3，X4，X5，X6，X7，X10｝，U′neg＝｛X9｝．划分后得U1＝｛X1，X2，X3｝，U2＝｛X4，X7，X10｝，U3＝｛X5，X6，X9｝．AS（1）＝ ｛d，ad｝，AS（2）＝ ｛a，ac｝，AS（3）＝｛d，ad｝，red（S1）＝｛d｝，red（S2）＝｛a｝，red（S3）＝｛d｝，按照文献［4］的思路，G＝｛｛a｝，｛d｝，｛d｝｝，POS｛b｝（D）≠POSC（D），又各子约简的最小基数都为1，则从G中随便取一个元素和属性b构成的集合便为最小约简，但POS｛a，d｝（D）≠POSC（D），POScore∪｛a｝（D）≠POSC（D），所以，文献［4］中的方法在此并不能求出最小约简．

按新算法有core＝｛a，d｝，因POScore∪｛a｝（D）＝POSC（D），所以core∪｛b｝＝｛a，b，d｝为所求．对于文献［4］中的例子，red（S1）＝∅，AS（2）＝｛a｝，red（S2）＝∅，AS（3）＝｛ab，ab｝，red（S3）＝ ｛｛a｝，｛b｝｝，故 core＝ ｛a｝，因 POScore∪｛c｝（D）＝POSC（D），故｛a，c｝为所求，结果与文献［4］相符．

6 结束语

本文提出一种时间复杂度为max（｜C｜｜U｜，K｜U1｜2＋ K｜U2｜2＋…＋ K｜Un｜2）的算法，该算法通过基于等价类的思想对决策表进行压缩，降低了计算的复杂性和存储空间，提高了算法的效率，在约简的时候采用基于核的思想，逐步求解，可以保证获得最小约简．

［1］吴明芬，许 勇，刘志明．一种基于属性重要性的启发式约简算法［J］．小型微型计算机系统［J］，2007，28（8）：1 452－1 455．

［2］颜 艳，杨慧中．一种基于互信息的粗糙集知识约简算法［J］．清华大学学报：自然科学版，2007，47（52）：1 903－1 906．

［3］王加阳，高 灿．改进的基于差别矩阵的属性约简算法［J］．计算机工程，2009，35（3）：65－67．

［4］叶明全，伍长荣．决策表分解及其最小属性约简研究［J］．计算机工程与应用，2009，45（30）：126－128．

［5］刘文军，谷云东，冯艳宾，等．基于可辨识矩阵和逻辑运算的属性约简算法的改进［J］．模式识别和人工智能，2004，17（1）：119－123．

［6］冯琴荣，苗夺谦，程 昳．决策表属性约简的相对划分粒度表示［J］．小型微型计算机系统，2008，29（12）：2302－2308．

［7］李订芳，李贵斌，章 文．基于U／｛a｝划分的最小约简构造［J］．武汉大学学报：理学版，2005，51（3）：269－272．

［8］徐章艳，刘作鹏，杨炳儒，等．一个复杂度为max（O（｜C｜｜U｜），O（｜C｜2｜U／C｜））的 快 速 属 性 约简算法［J］．计算机学报，2006，29（3）：391－399．