如何用SAS软件正确分析生物医学科研资料XV.用 SAS 软件实现具有一个重复测量的两因素和具有两个重复测量的两因素设计定量资料的统计分析
王琪,胡良平,高辉
我们曾详细介绍了如何用 SAS 软件实现具有一个重复测量的单因素设计定量资料的统计分析。本期,我们继续探讨生物医药研究中最常见的其他两种重复测量设计,即具有一个重复测量的两因素和具有两个重复测量的两因素设计定量资料的统计分析的SAS 实现。
1 具有一个重复测量的两因素设计定量资料的SAS 实现
例1 选了 10只家兔观察某药物 A 对皮肤损伤情况。A有 2个水平:A1(高浓度),A2(低浓度);为了排除实验部位对观测结果的影响,药物涂在兔的4个对称部位上,即部位因素 B 有 4个水平:B1(左前腿)、B2(右前腿)、B3(左后腿)、B4(右后腿)。10只家兔被完全随机地均分到 A1、A2两组中去,将药物涂在任何一只兔 4条腿的对称部位上、且涂的面积相等,资料见表1,试进行合适的统计分析。

表1 家兔皮肤损伤直径
分析与SAS 实现:本例涉及“药物浓度”和“部位”两个实验因素,由于是在用药后从同一只兔的不同部位重复获得指标“皮肤损伤直径(mm)”的观测值,所以,“部位”是一个重复测量因素,资料所对应的实验设计类型为具有一个重复测量的两因素设计。
具体的SAS 程序如下:

data sastjfx1; /*1*/do A=1 to 2;do rabbit=1 to 5;do B=1 to 4;input y @@; output;end; end; end;cards;16.520.718.319.516.719.017.918.416.518.516.417.618.022.519.220.217.520.018.719.918.221.219.418.918.520.519.618.3 proc mixed data=sastjfx1; /*5*/class A rabbit B;model y=A|B;repeated/type=AR(1) sub=rabbit(A);ods output fitstatistics=d;ods output dimensions=d1;run;%MACRO SHUJU(dataset,y); /*6*/data &dataset;set &dataset;&y=value;drop value;run;%MEND SHUJU;

19.722.521.320.521.523.722.421.920.722.721.621.8;run;proc mixed data=sastjfx1; /*2*/class A rabbit B;model y=A|B;repeated/type=VC sub=rabbit(A);ods output fitstatistics=a;ods output dimensions=a1;run;proc mixed data=sastjfx1; /*3*/class A rabbit B;model y=A|B;repeated/type=CS sub=rabbit(A);ods output fitstatistics=b;ods output dimensions=b1;run;proc mixed data=sastjfx1; /*4*/class A rabbit B;model y=A|B;repeated/type=UN sub=rabbit(A);ods output fitstatistics=c;ods output dimensions=c1;run;%SHUJU(a,VC) %SHUJU(b,CS)%SHUJU(c,UN) %SHUJU(d,AR1)%SHUJU(a1,VC) %SHUJU(b1,CS)%SHUJU(c1,UN) %SHUJU(d1,AR1)data e; /*7*/merge a b c d;run;data e1; /*8*/merge a1 b1 c1 d1;run;ods html;proc print data=e; /*9*/format _numeric_ 5.1;run;proc print data=e1; /*10*/run;ods html close;
程序说明:SAS 程序中第 1 步为建立数据集;A 代表“药物浓度”;B 代表“部位”;rabbit 代表“受试动物个体”;y 代表观测指标“直径”。第 2、3、4、5 步分别调用 mixed过程,采用 VC、CS、UN、AR(1) 四种协方差结构模型对资料进行方差分析。第 6 步为建立宏 SHUJU,以实现对数据集中已有变量 value的更名。第 7、8 步均用来实现对不同数据集的横向合并。第 9、10 步均用来将数据集中的内容输出到 output 窗口中去。第 2、3、4、5 步所用语句基本相同,仅在“type=”后的选项不同,4个过程分别指定了 4 种协方差结构模型。Mixed 过程中 repeated 语句用来规定个体的重复测量的协方差结构,“/”后的sub(也可写为subject)用来指定数据集中的个体,若不含有分组因素,直接在“sub=”后面给出受试对象个体变量名称即可;若含有分组因素,则在“sub=”后面给出受试对象个体变量名称的同时,还需在后面加注“()”,括号内填入分组变量名称。在调用 mixed 过程进行方差分析时,使用了两个 ods(output delivery system)语句,分别用来将模型拟合的有关信息(fitstatistics)和模型维度有关参数(dimensions)输出。
SAS 输出结果与结果解释:

Obs Descr VC CS UN AR11 –2 Res Log Likelihood 119.9 81.2 73.0 87.82 AIC (smaller is better) 121.9 85.2 93.0 91.83 AICC (smaller is better) 122.0 85.6 103.5 92.24 BIC (smaller is better) 122.2 85.8 96.0 92.4

Obs Descr VC CS UN AR11 Covariance Parameters 1 2 10 22 Columns in X 15 15 15 153 Columns in Z 0 0 0 04 Subjects 10 10 10 105 Max Obs Per Subject 4 4 4 4
这是上述程序中 ods 输出的结果。首先给出了 4 种协方差结构模型拟合本资料的有关情况,然后给出了协方差阵的有关信息(Covariance Parameters 表示模型中待估计的协方差结构中参数的个数)。比较 4 种模型拟合资料情况的AIC、BIC 数值,可发现 CS 与UN 两种协方差结构模型拟合资料较好。现比较这两种协方差结构模型拟合资料的效果之间的差异是否有统计学意义。

由ods 输出结果的第二部分可知,q=2,q+v=10,所以v=8。而=15.51>8.2,故P>0.05。认为可以选择参数个数较少的协方差结构模型,所以最后的结论应按CS协方差结构模型计算出来的结果来下。其假设检验结果为:

Type 3 Tests of fixed effects
由上述结果可知:药物浓度(A)、部位(B)、药物浓度与部位的交互作用(A*B)均有统计学意义。
欲得出各均数之间两两比较的结果,可将原程序中所有过程步删除,换上以下过程步:

程序运行后,得如下结果:

Least squares means
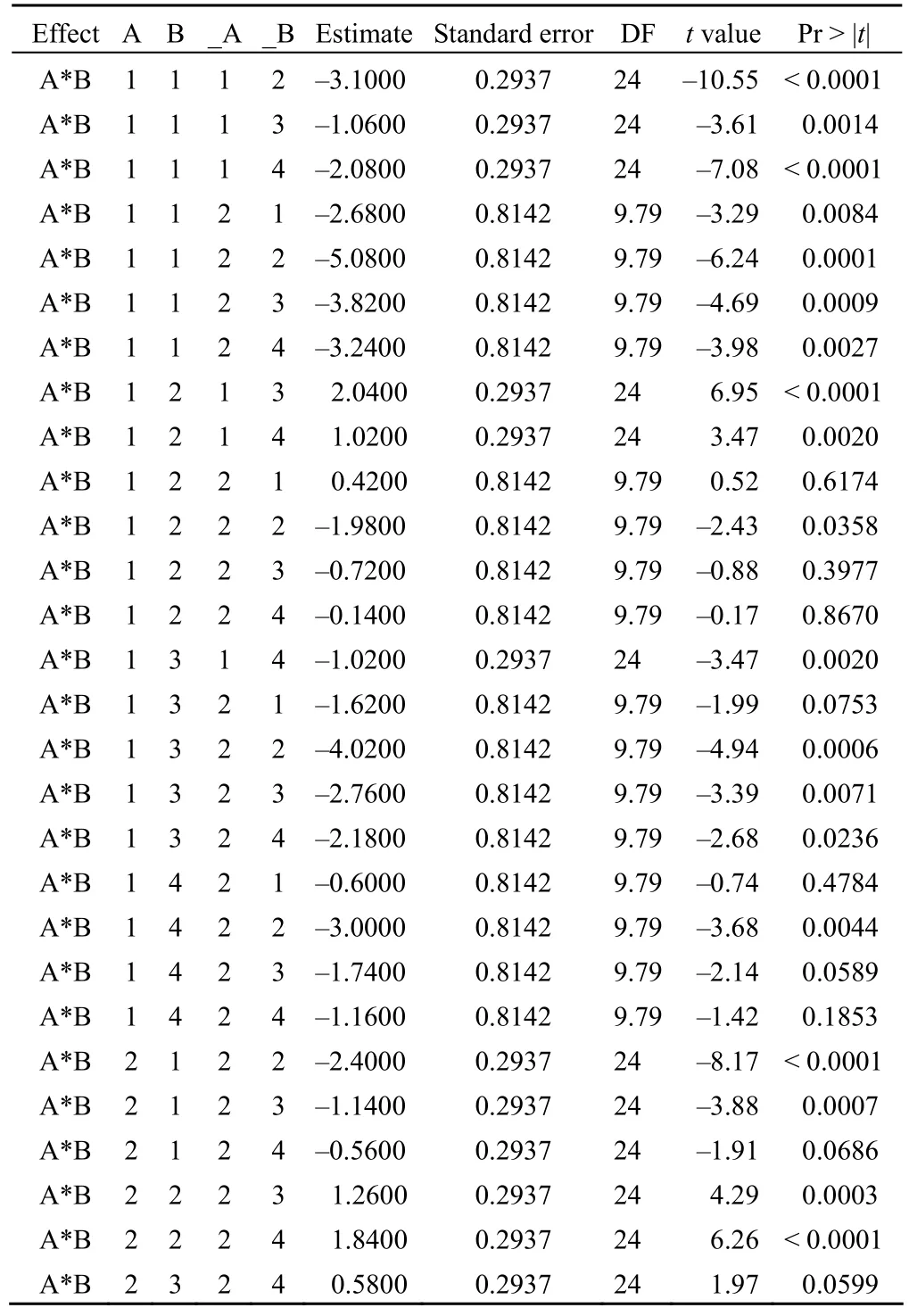
Differences of least squares means
这是两种药物浓度的受试对象各部位皮肤损伤直径均值之间两两比较的结果,首先给出了每种药物浓度的受试对象各部位皮肤损伤直径均值与0 比较的检验结果,没有任何实际意义。后面给出了两两比较的结果,A和B 列指定其中的某药物浓度受试对象某个部位上的数据,_A和_B列也指定其中的某药物浓度受试对象某个部位上的数据。
2 具有两个重复测量的两因素设计定量资料的SAS 实现
例2 用5 条狗在背部做成同样大小创伤 3个,分别用 3种药物 A1、A2、A3治疗,在用药后第 2、4、6、8 天 4个时间点上(分别用 B1~B4表示)观测创伤面积(cm2)。目的是观察药物对创伤面积影响的动态变化情况,资料见表2,试进行合适的统计分析。
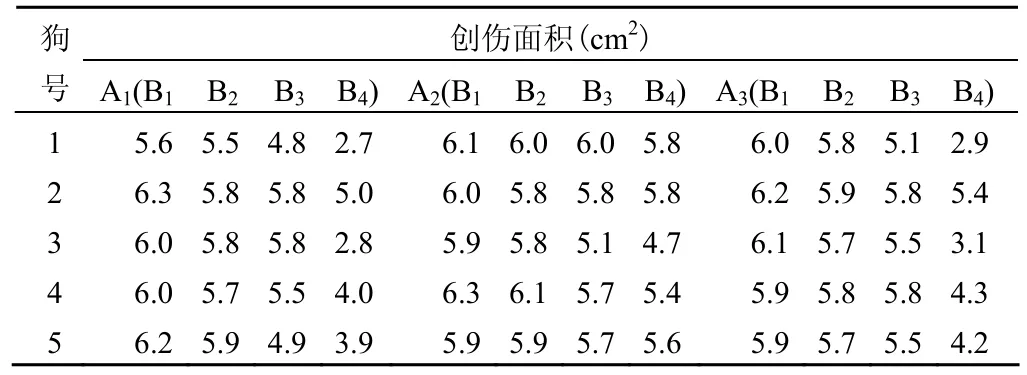
表2 3 种药物使用后不同时间点上观测到的创伤面积
分析与SAS 实现:该资料涉及“药物种类”和“药物作用时间”两个实验因素,由于是在同一只狗身上重复使用3 种药物(每种药用在一个创伤部位),并在用药后4个不同的时间点上重复测得每一处创伤的创伤面积,所以,“药物种类”和“药物作用时间”都是重复测量因素,该资料所对应的实验设计类型为具有两个重复测量的两因素设计。观测指标为“创伤面积(cm2)”,是定量指标,故应选用具有两个重复测量的两因素设计一元定量资料的方差分析来处理此资料。
具体的SAS 程序如下:

data sastjfx2; /*1*/do dog=1 to 5;do drug=1 to 3;do time=1 to 4;input y @@;output;end; end; end;cards;5.65.54.82.76.16.06.05.86.05.85.12.96.35.85.85.06.05.85.85.86.25.95.85.46.05.85.82.85.95.85.14.76.15.75.53.16.05.75.54.06.36.15.75.45.95.85.84.36.25.94.93.95.95.95.75.65.95.75.54.2;run;proc mixed data=sastjfx2; /*2*/class dog drug time;model y=drug|time;repeated/type=VC sub=dog;ods output fitstatistics=a;ods output dimensions=a1;run;proc mixed data=sastjfx2; /*3*/class dog drug time;model y=drug|time;repeated/type=CS sub=dog;ods output fitstatistics=b;ods output dimensions=b1;run;proc mixed data=sastjfx2; /*4*/class dog drug time;model y=drug|time;repeated/type=AR(1) sub=dog;ods output fitstatistics=c;ods output dimensions=c1;run;ods html;proc sql; /*5*/select a.Descr,a.VALUE as VC,b.VALUE as CS, c.VALUE as AR1 from a,b,c where a.Descr=b.Descr=c.Descr;quit;proc sql; /*6*/select a1.Descr,a1.VALUE as VC,b1.VALUE as CS, c1.VALUE as AR1 from a1,b1,c1 where a1.Descr=b1.Descr=c1.Descr;quit;ods html close;
程序说明:SAS 程序中第 1 步为建立数据集;dog 代表“狗号”;drug 代表“药物种类”;time 代表“药物作用时间”;y 代表观测指标“创伤面积”。第 2、3、4 步分别调用 mixed 过程,采用 VC、CS、AR(1) 三种协方差结构模型对资料进行方差分析。第 5、6 步将不同数据集的内容进行合并查询,这与上一个程序中的宏 SHUJU 功能相同。由于采用 UN 协方差结构模型对资料进行方差分析时,中间计算无法形成正定矩阵,分析过程中断。所以,上面没有给出用 UN 协方差结构模型对资料进行方差分析的程序。而 SP(POW)要求重复测量因素均为定量变量,本资料中的药物种类是一个定性变量,所以也没有采用 SP(POW)协方差结构模型对资料进行方差分析。
SAS 输出结果与结果解释:

Description VC CS AR1–2 Res Log Likelihood 84.6 78.4 79.9 AIC (smaller is better) 86.6 82.4 83.9 AICC (smaller is better) 86.6 82.6 84.1 BIC (smaller is better) 86.2 81.6 83.1 Description VC CS AR1 Covariance Parameters 1 2 2 Columns in X 20 20 20 Columns in Z 0 0 0 Subjects 5 5 5 Max Obs Per Subject 12 12 12
这是上述程序中 ods 输出的结果。首先给出了 3 种协方差结构模型拟合本资料的有关情况,然后给出了协方差阵的有关信息。比较 3 种模型拟合资料情况的AIC、BIC 数值(越小越好),可发现 CS 协方差结构模型拟合资料较好,而 VC 协方差结构模型拟合资料效果虽不如 CS 协方差结构模型好,但其模型中参数个数要比 CS 协方差结构模型少。现比较这两种协方差阵模型拟合资料的效果之间的差异是否有统计学意义。

由 ods 输出结果的第二部分可知,q=1,q+v=2,所以v=1。而=3.84>6.2,故 P>0.05。可认为不适合用VC模型取代CS 模型,所以最后的结论应按CS协方差结构模型计算出来的结果来下。其假设检验结果为:

Type 3 Tests of fixed effects
由上述结果可知:药物种类(drug)、药物作用时间(time)以及两者的交互作用(drug*time)均有统计学意义。即不同时间点上测得的家犬创伤面积均值之间的差异有统计学意义,不同药物对创伤面积均值影响之间的差异有统计学意义。
欲得出各均数之间两两比较的结果,可将原程序中所有过程步删除,换上以下过程步:

此步运行结果与上述 type=CS 过程步计算结果基本相同,仅多了多个均数两两比较的结果,输出结果所占篇幅较多,此处从略。
需要说明的是:有些重复测量设计定量资料中含有协变量,如实验中对每一个个体在不同的时间点上进行了重复测量,其中在“服药前”观测了 1 次,在“服药后”观测了 k(k ≥ 2)次,这属于带有协变量的重复测量设计问题。对这类资料,最合适的分析方法是以服药前观测的结果作为“基础值”(即作为“协变量”),采用带有协变量的重复测量设计资料定量资料的协方差分析。当然,对于具有一个重复测量的单因素设计定量资料,由于再无其他实验分组因素,故即便含有“基础值”,也不需要采用协方差分析。关于带有协变量的重复测量设计定量资料的统计分析问题,请读者参考相关文献。
[1]Hu LP.Application of statistical triple-type theory in the experiment design.Beijing: People’s Military Medical Press, 2006:107-120.(in Chinese)胡良平.统计学三型理论在实验设计中的应用.北京:人民军医出版社, 2006:107-120.
[2]Hu LP.Scientific research design and statistical analysis of cardiovascular disease.Beijing: People’s Military Medical Press,2010:93-111.(in Chinese)胡良平.心血管病科研设计与统计分析.北京:人民军医出版社,2010:93-111.

