小学数学化归思想研究述评
马 旭
(云南民族大学 教育学院,云南 昆明 650500)
小学数学化归思想研究述评
马 旭
(云南民族大学 教育学院,云南 昆明 650500)
对有关化归思想在小学数学中的渗透的文献进行了分类整理和归纳分析,分别就化归思想在小学数学教材、教学、解题中的渗透这三方面进行了文献梳理,总结了当前化归思想在小学数学中渗透所取得的成果及存在的不足。
化归思想;小学数学
一 化归思想简介
“化归”从字面上看,指的就是转化和归结的意思。而在数学方法论中,化归指的是数学家们把待解决的或未解决的问题,通过一定的转化过程,归结到一类已经能解决或者比较容易解决的问题中去,最终获原问题的解答的一种手段和方法。化归方法同时也称为化归原则。
下面我们看一个例子:
有人提出了这样一个问题:“假设在你面前有煤气灶、水龙头、水壶和火柴,你想烧开水,应当怎样去做?”对此某人回答说:“在壶中灌上水,点燃煤气,再把壶放到煤气灶上。”提问者肯定了这一回答;但是,他又追问道:“如果其他的条件都没有变化。只是水壶中已经有了足够多的水.那你又应当怎样去做?“这时被提问者往往会很有信心地说:“点燃煤气,再把水壶放到煤气灶上。”但是,提问者指出,这一回答并不能使他满意,因为,更好的回答应当是:“只有物理学家才会这样做,而数学家们则会倒掉壶中的水,并声称我把后一问题化归为前面所说的问题了。”(史久一,朱梧槚,1989)
这个故事看起来像一个笑话,但是它正好反映出了数学解题过程中人们普遍采用的一种手段与方法,也就是通过一系列的转换的方法与手段把遇到的新问题转化为过去曾经解决过的问题,依托曾经解决过的问题来解决新的问题。
在数学史上,有不少数学家也从各种不同的角度对化归方法进行过论述。笛卡尔在《指导思维的法则》一书中就曾提出过如下的“万能方法”:
第一,将任何种类的问题化归为数学问题;
第二,将任何种类的数学问题化归为代数问题;
第三,将任何代数问题化归为方程式的求解。
因此在小学阶段,将化归思想介绍给学生,让学生掌握这一方法显得尤为重要。我们不仅要向学生传授基本知识,基本技能,更重要的是使学生掌握更多的数学思想,数学方法。这将有助于学生今后的学习与发展。
二 化归思想在小学数学中的渗透
化归方法是一种通过转换间接解决问题的方法。它在数学问题解决中的作用就在于转化,转化问题是解决问题的关键,转化的思想就是化归的思想。问题的解决过程就是不断地发现问题、分析问题,直至化归为一类已经能解决或者比较容易解决的问题的过程。化归方法在数学问题解决中具有十分重要的意义。这已经被很多人所意识到。尤其是将化归思想渗透到小学数学中,已经被越来越多的人所重视。以下是化归思想在小学数学中的一些具体运用。
1.化归思想在小学数学教材中的渗透。
化归思想体现在小学数学教材的各个方面。
(1)在数与代数方面。结合数的认识教学,渗透化归数学思想方法。“数的认识来源于生活,又应用于生活”(叶锦红,林丹,2010)。小学数学教材选取问题的范围大都来源于学生密切接触的现实生活,在此我们可以随便举个例子 。
例如,人教版小学数学三年级下册第7课《小数的初步认识》。

图1①
对小数的认识从学生密切接触的现实生活入手,学生开始的时候不知道小数这一概念,但是在现实生活中肯定是买过东西的。并且商品的价格不全是整数,因此通过教材这一媒介,将学生们现实生活中经常遇到不加注意的材料联系起来。并且通过这样一种从生活中来,并应用于生活的学习,加深对于知识的学习。
(2)空间与图形。“对于平行四边形面积计算的研究课例中已具体说明,主要通过现实问题具体化到抽象问题,然后在抽象与具体间建立联系,从而实现抽象向具体的化归,同时利用割补、平移等化归途径,自主将复杂问题简单化成求长方形的面积”(叶锦红,林丹,2010)。图形的计算就在于图形的变换,恰当的变化与转化使得图形的计算变得尤为简便。而在小学阶段,对于新图形的认识,最好的办法就是将它转化为已经学过的图形。

图2②
正如平行四边形的学习一样,复杂图形的学习很重要的一个方法就是将其分解成简单图形,正是这种化繁为简的方法,为以后的几何学习打下了一定的方法基础。
正如前面所谈到的化归思想大量地渗透到了小学数学教材中。所以,“教师要认真研读教材,透过显性的教学内容挖掘隐藏的数学思想方法”。(李放,2010)
2.化归思想在小学数学教学中的渗透。
首先,在小学数学教学中渗透化归思想,可以通过“创设问题情境”的方法。(李放,2010;叶锦红,林丹,2010)通过创设一定的问题情境,提高同学们的积极性。将一些抽象的问题具体化,使得同学更容易理解所要学习的内容。
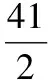
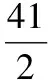
针对两种情况,再分别算出各跳了几次, 确定谁先掉人陷阱,问题就基本解决了。
上面的思考过程,实际上是把一个实际问题通过分析转化、归结为一个求“ 最小公倍数” 的问题, 即把一个实际问题转化、归结为一个数学问题。因此可以通过创设一定的问题情境在教学过程中将化归思想融入问题之中。使学生清楚地掌握化归思想。
其次,“在学生知识的发生过程中渗透化归思想”。(李放,2010)也就是人们通常所说的在知识的产生、推导与转化过程中渗透化归思想。
例如,平行四边形的面积计算:长方形的面积是长乘宽,那么平行四边形的面积该如何计算呢?在同学们剪拼的过程中,把平行四边形转化成长方形,并引导他们思考:平行四边形与拼成的长方形有什么关系?最后得出:平行四边形的面积=底×高。
通过转化,将未知的问题转化为已知的问题,最后达到解决问题的目的。这一过程不仅是一个得到最终答案的过程,更为重要的是使学生学会了一种解决问题的方法。学会这一方法之后在今后的学习中碰到类似的问题,便能够轻而易举地解决了。对于教师的教学“不在于教什么,而真正在于怎样教”(Ricardo Cantoral amp; Rosa M. Faran,2003)。
3.化归思想在小学数学解题过程中的渗透。
数学学习一个主打的方面便是数学问题的解决——解题。数学无论从学习入手,还是最终学习情况的考核,主要就是看解题的能力。化归思想也正是在解题过程中才能充分体现出来。因此,大量的目光也就聚焦到数学问题的解决这一领域上来。
“在各类试题的学练中, 要用符号思想、模型思想等, 使学生正确、灵活、迅速地掌握各种运算法则、性质、定律、顺序等,使试题的学练成为学生解决各类实际问题的可靠工具”。(安君丽,2001)“在解决问题中体验数学思想方法,运用数学思想方法可以更有效地解决问题”。(李放,2010)人们不但意识到了化归思想在解题过程中的作用,同时也总结出了一些化归思想在解题过程中的方法。“即把一个实际问题转化、归结为一个数学问题”。杨莉(2005)也就是通常所说的数学建模,将生活中的问题利用数学方法加以解决。其本质也体现了学以致用的一般原则。而吴生莲(2009)则将其具体化为“数据转化、图形转化、题型转化”三大类型。可以说是比较具体地分析了在小学数学解题过程中存在的各类情况。
但在利用化归思想的同时我们也必须明确一点“这种化归思想不同于一般所讲的‘转化’‘转换’。它具有不可逆转单向性。”(杨莉,2005)
三 化归思想渗透到小学数学的问题
通过上面的介绍,我们大体明确了化归思想渗透到小学数学中的三种方式。但是我们在具体运用化归思想的时候还得注意一些问题。
第一,使未知问题熟悉化。我们使用化归思想解决问题时必须要将我们所遇到的新问题转化为一个或几个我们所熟悉的问题,即将陌生的问题转化为我们已经熟悉的,在过去的时间内已经解决过的问题,这样一来,我们就能够将待解决的问题依托于我们曾经使用过的方法来解决。同样,我们在教学生的时候也应该将新问题转化为学生以前学习过的问题,会的问题。这样一来也能把新旧问题连接起来使知识产生连贯性,系统性。从教材的编排上我们也能够看出来,小学数学主要围绕三大部分:数与代数、空间与图形、数理统计。从一年级到六年级都围绕着这三大部分。通过问题的转化便能将知识以一个脉络连接起来。
第二,将问题简单化。化归思想是一种解决问题的手段与方法,因此,我们在使用过程中肯定应该选一条捷径来走,原问题困难,我们就教给学生想办法将其简单化,从上面的例子我们也可以看出来,将平行四边形转化为三角形与矩形时就遵循了这样一个原则。简单化原则也提醒我们在使用化归思想时,不要将原问题复杂化,原来很简单的问题,我们不能反倒将其转化为一个更困难的问题去求解。
第三,将问题具体化。有些问题很抽象,我们可以使用一些诸如数形结合的方法,将一些不明显、比较抽象的问题使用图形来表示,来解决。这样一来,我们便可以将原问题清晰具体地反映出来,通过具体问题的解答,将原问题加以解决。这一原则在下面具体阐述化归思想的应用过程中将予以体现。
第四,正难则反。正难则反,也就是我们通常意义上的反证法。原问题的条件给了我们一种思路,但是依靠这一思路我们很难将问题解决了,因此,我们可以换一种思路,原问题让我们向前走,我们可以想想,如果向后退情况会是什么样呢?在我们解决一些问题过程中我们可以使用例如反证法这样的一些手段,将问题转化到问题的另一面加以解决。
四 总结
通过梳理我们已经明确了化归思想渗透到小学数学中的三种方式:通过教材的编写渗透,通过教师的教学渗透以及通过解题过程渗透。通过这三种方式,可以很好地使学生掌握化归思想这一重要的思想方法。这也在一定程度上告诉我们可以从哪几个方式入手将化归思想传递给学生。通过课堂,可以更好地发挥教师的主导地位与学生的主体地位,使学生掌握化归思想。
但同时我们也能够看出目前化归思想在小学数学中的渗透主要是靠教师的知识传递。也正是在教师传授的过程中出现了很多问题,这便是教师的满堂灌,使学生盲目接受知识,而不加思考。因此,使学生掌握化归思想只有发挥学生的主动性。培养让学生在自学过程中,自觉地使用化归思想。这样才能最大限度地发挥学生的创造性思维。鼓励学生自觉运用化归思想将是以后研究的重点方向。
同时,如今是一个学习型的社会,知识的学习也不能仅仅靠个人的埋头苦读,而是需要组成一定的学习团队,形成一定的学习小组。鼓励学生形成一种合作学习的学习方法,让学生对于新的学习问题形成一种“合作的视角”(Cindy E. Hmelo-Silver ,Ellina Chernobilsky amp;Rebecca Jordan,2008),将是今后教学的重中之重。也正因为如此,化归思想的渗透同样需要教师有意识地在班级里组建学习小组,通过小组成员间的相互学习来掌握化归思想。这也将是今后关注的焦点之一。
注释
①http://www.pep.com.cn/xxsx/xxsxjs/xs3b/xs3bkb/200703/t20070314_339024.htm.
②http://www.pep.com.cn/xxsx/xxsxjs/xs4a/xs4akb/200704/t20070411_388604.htm.
[1]史久一,朱梧槚.化归与归纳·类比·联想[M].南京:江苏教育出版社,1989:141-190.
[2]成尚荣. 学会数学地思维——小学数学教学案例解读[M].南京:江苏教育出版,2001:148-186.
[3]张甦,朱英.数学思想方法[M].上海:上海科学普及出版社,2009:26-87.
[4]安君丽.新世纪小学数学教学的精髓[J].教育实践与研究,2001(11),53.
[5]杨莉. 小学数学教学中如何渗透数学思想方法[J].科学咨询(教育科研), 2005(03): 51.
[6]陈桂娣. 数学思想方法: 小学数学教学不可忽视的灵魂[J].黑龙江科技信息,2007(03): 115.
[7]于占武.化归思想在解题中的应用[J].赤峰学院学报,2007(10): 24-25.
[8]凌健.化归思想在数学解题中的应用[J].安庆师范学院学报 ,2008(2): 511.
[9]吴生莲.例谈化归思想方法在解题中的渗透[J].小学教学参考(数学),2009(10): 59.
[10]李放.渗透数学化归思想提高问题解决能力[J].新课程研究 ,2010(06):122-124.
[11]叶锦红、林丹. 数学化归思想在小学数学教学中的应用[J].科研纵横 , 2010(08):26-27.
[12]Ricardo, C. , amp; Rosa, M. F.(2003).Mathematics education:a vision of its evolution. Educational Studies in Mathematics, 53:255-270.
[13]Cindy E. Hmelo-Silver , Ellina C. amp; Rebecca J.(2008). Understanding collaborative learning processes in new learning environments. Instructional Science, 36:409-430.
ClassNo.:G623.5DocumentMark:A
(责任编辑:宋瑞斌)
ReviewoftheIdeaofConversioninMathematicalEducationinPrimarySchool
Ma Xu
Firstly, classification and an inductive analysis are made through systematic research literature of the permeation of the idea of conversion in mathematical education in primary school. Secondly, a literature review of permeation is made in the following three aspects: 1) textbook 2) instruction and 3) solving problems in mathematical education in primary school. Finally, achievements and Limitations in current studies on the permeation of the idea of conversion in mathematical education in primary school are summarized.
idea of conversion;mathematical education in primary school
马旭,硕士,云南民族大学教育学院。
1672-6758(2012)09-0007-3
G623.5
A

