水平受荷桩1g模型试验变形特性的相似分析
林海,雷国辉,徐林,雷国刚
(1.河海大学 岩土力学与堤坝工程教育部重点实验室/岩土工程科学研究所,江苏 南京,210098;2.南京市水利建筑工程总公司一公司,江苏 南京,210036)
室内物理模拟实验中模型与原型的相似性分析是实验设计的基础,也是理解实验结果并应用于原型的关键。几何相似、运动相似、动力相似以及本构相似是实验结果相似的充分和必要条件。现有文献中,针对离心模型实验中模型与原型的相似性分析受到普遍重视,但是,相比而言,针对1g模型实验中模型与原型的相似性分析却并未引起足够重视(其中 g为重力加速度,1g=9.8 m/s2)。其主要原因在于:岩土材料的力学性质依赖于其应力状态,而缩尺后的1g模型使得本构相似难以满足,进而使得运动相似和动力相似也难以满足。尽管如此,1g模型实验在岩土工程问题的研究中仍然可以应用并发挥着重要作用,Randolph等[1]对此有专门的阐述。合理地应用1g模型实验的关键在于充分认识其中的相似性关系对于所研究的问题可以近似满足。桩基的模型实验研究已有大量文献报道[2]。针对1g模型实验中的竖向受荷桩,Sedran等[3]分析了模型与原型的相似性关系,结果表明:模型与原型的摩阻力相似比(即应力比)等于几何相似比而不等于 1,不满足运动相似的强制性条件,因此,竖向受荷桩1g模型摩阻力实验结果的合理性值得怀疑。针对水平受荷桩,Franke[4]分析了1g模型实验可以用于荷载位移关系中一些无量纲数的确定,即满足模型与原型的相似性。但是,对于如图1所示的刚性桩和柔性桩这2种截然不同的变形特性,其相似性却有明显的差异。显然,模型桩与原型桩具有相同的变形特性是水平受荷桩模型与原型相似的必要条件。为此,本文作者运用刚性桩和柔性桩临界桩长的判别公式,根据相似性原理,分析研究模型桩与原型桩满足相同变形特性的相似性条件和评判方法,并提出改善水平受荷桩模型试验相似性的办法。

图1 桩头自由时水平受荷桩的2种变形形式Fig.1 Two deflection types of laterally loaded free-head piles
1 水平受荷桩变形类型的判别
桩的长径比和桩土刚度比是影响水平受荷桩变形特性的主要因素。当桩的长径比较小、桩土刚度比较大时,桩身的变形特性主要由桩周土的力学性质所决定,通常发生的是如图 1(a)所示近似于刚体的转动变形,这类桩被称之为刚性桩。当桩的长径比较大或桩土刚度比不大时,桩身的变形特性主要由桩体材料的力学性质所决定,通常发生的是如图1(b)所示沿深度呈波状曲线逐渐消减的挠曲变形,当桩身出现2个以上位移零点和弯矩零点时,这类桩被称为柔性桩。介于这2种变形特性之间的被称为半刚性桩[5]。
工程上,为判别刚性桩和柔性桩,通常采用临界桩长的计算公式。当桩的入土深度l小于刚性桩的临界桩长lc,r时,为刚性桩;当l大于柔性桩的临界桩长lc,f时,为柔性桩;当 l介于 lc,r和lc,f之间时,为半刚性桩。现有的研究成果中,临界桩长的计算公式根据水平受荷桩的计算方法不同而具有不同的表达式。
对于地基反力法,Tomlinson[6−7]假定砂土和正常固结黏土的地基土反力系数kh随深度z线性增加的计算模式(即kh=nhz/b,其中nh为地基反力系数随深度增加的比例系数,量纲为[F][L]−3;b为桩身直径或垂直于荷载作用方向的桩身宽度),得到的临界桩长公式为:

式中:Ep和Ip分别为桩身的弹性模量和截面惯性矩。
对于埋置于超固结硬黏土中的水平受荷桩,Tomlinson等[6−7]假定地基土反力系数kh为常数,得到的临界桩长公式为:
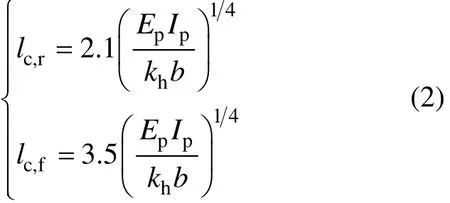
而对于弹性理论法,Poulos等[7]假定土体的弹性模量Es随深度线性增加的计算模式(即Es= nsz,其中 ns为弹性模量随深度增加的比例系数),推求的临界桩长公式按照上述形式可表达为:

假定Es为不随深度变化的常数时,Poulos等[7]得到的临界桩长公式为:

Meyerhof等[8]在砂土和黏土中分别做了直径d为12.5 mm的钢桩、木桩和尼龙桩的模型试验。试验采取改变桩体的埋深(l/d=8,15,24和48),并且使得模型桩的埋置深度分别处在临界桩长 lc,r的两端,试验结果证实临界桩长的表达式对模型桩也具有普遍适用性。
除了上述由地基反力法和弹性理论法给出的临界桩长公式外,还有一些其他刚性桩和柔性桩临界桩长的判别公式,如 Randolph[9]基于有限单元法和吴恒立[10]基于双参数法提出的临界桩长公式等。下面将以上述列出的临界桩长公式为例,示范分析水平受荷桩满足相同变形特性的相似性条件。
2 1g条件下的缩尺模型桩
在文献中可以找到大量的关于水平受荷桩的模型试验,但正如Altaee等[11]所言,1g试验很少论述模型所对应的相似原型,或者研究模型试验的结果能否反映现场大尺寸桩基。根据相似理论,若缩尺模型与原型之间的相似条件不满足,则二者不存在相似性。
采用地基反力法的计算模式,水平受荷桩1g模型试验与对应原型的参数及他们之间的相似关系如表 1所示。按照几何相似条件,几何相似比λl与λb是相等的,且有桩身截面惯性矩相似比 λI=λl4。考虑到土体力学性质的复杂性,模型试验中模型土通常采用原型土。桩周土为砂土的情况下,将计算参数代入Broms的临界桩长表达式(1)可分别得到原型与模型的刚性桩临界桩长公式为:


由式(5)和(6)可以求得砂土中1g缩尺模型桩的刚性桩临界桩长相对原型的相似比λT为:

若缩尺模型桩和模型土都采用与原型相同的材料时(λE=1,nh相同),则由式(7)可以得到模型桩的刚性桩临界桩长相似比为而缩尺模型桩的实际入土深度相似比为λl。显然,临界桩长的相似比λT小于几何相似比 λl,这意味着,当原型桩为非刚性桩时,缩尺后的模型桩却有可能为刚性桩。用此类刚性桩的试验去反映现场原型的非刚性桩是不正确的,变形类型发生改变的1g缩尺桩基模型与原型不相似,试验结果不可用来推测原型桩的性状。

表1 缩尺1g模型桩的参数Table 1 Parameters of 1g reduced-scale model pile
类似地,对于超固结硬黏土,Terzaghi得到地基反力系数kh与不排水剪切强度有关且可近似认为沿深度不变[6]。由公式(2)得到原型与模型的刚性桩临界桩长为:

由式(8)和(9)可以求得超固结硬黏土中1g缩尺模型桩的刚性桩临界桩长相似比λT为:

当缩尺模型桩和模型土都采用与原型相同的材料时(λE=1,kh相等),与前面的分析类似,1g缩尺模型水平受荷桩的变形特性与原型桩的变形特性则有可能不同。
采用弹性理论法临界桩长公式(3)和(4)或其他方法评价水平受荷模型桩与原型桩的变形特性,也能够得到类似的分析结果。总之,采用与原型相同的桩材和土来开展的模型试验,缩尺模型桩的临界桩长相似比λT小于几何缩尺比λl,即模型桩较原型桩表现得更为刚性。
3 相似分析
对水平受荷桩 1g模型与原型之间进行相似性分析,可以判别能否开展相似的缩尺模型试验或得到开展相似模型试验的条件。水平受荷桩模型的相似性包括4个方面:几何相似、运动相似、动力相似以及本构相似。
2系统的几何尺寸对应成比例称为几何相似。水平受荷模型桩的入土深度、桩身计算宽度、桩头伸出地面距离等都应按相等比例缩小。土体作为一种最常见的地基材料,不同的颗粒级配会改变土体的物理力学性质,因此,模型土颗粒的粒径不能按几何相似比缩小,模型无法满足严格的几何相似。对于这种由土体颗粒尺寸造成的缩尺效应,有许多学者对其进行了研究。Franke等[6]根据Ovesen在砂土中进行的一系列圆形基础试验得出:当基础直径B与砂土的特征粒径d50比值大于30时(B/d50≥30),可以忽略土颗粒不缩小的影响。Floravante等进行了一系列竖向荷载作用的桩基离心试验,得到当桩径B与土体的特征粒径d50的比值大到一定程度时,可以忽略土颗粒的缩尺效应[12]。Floravante[12]进行了砂土中钻孔灌注桩的离心试验,通过开展4组不同桩径B与砂土特征粒径d50比值的圆桩试验(B/d50=27,46,64,108),验证了当B/d50的值大于某临界值时可以忽略土颗粒的缩尺效应,且认为B/d50临界值取40~50较为适宜。同样,在开展水平受荷桩缩尺模型试验时,只要能够保证模型桩的短边尺寸大于土体特征粒径 d50的一定倍数时,可以忽略土颗粒尺寸不缩小的影响,近似地认为模型满足几何相似。
运动相似及动力相似直接体现为原型和缩尺模型满足相同的控制方程。运动相似考虑了运动的时间效应,主要针对动荷载作用下的水平受荷桩。本研究主要分析静力作用下的水平受荷桩模型与原型间的相似性,不考虑此类相似的情况。水平受荷桩1g模型与原型的动力相似要求二者为同样的变形类型。由式(7)和(10)可知:若能够使得桩身弹性模量相似比λE=λl而非λE=1,则能够使得1g模型在理论上与原型变形相似。
本构相似为材料的应力应变关系相似,对于桩身材料,近似认为其表现为线弹性,则其应变与初始应力无太大关系。王馥廷等[13]在综合刚度原理双参数法的基础上对水平受荷桩模型动力相似分析得到,相似缩尺模型应该用细砂或中砂去模拟原型的砾砂或卵石等。这是从找寻合适模型土的角度去满足相似性,但是这种方法的正确性存在疑问。细、中砂与卵石间的力学性质差异很大,它们之间不存在本构相似。考虑到土的应力应变关系本身的复杂性和实验室开展模型试验时取土的容易程度,模型试验用土采取原型同种土。土的性质与应力状态相关,而1g模型中的竖向应力存在缩尺,从而使得 1g模型的本构相似无法严格满足。
即便这样,由于水平受荷桩的应力影响分布主要在于水平方向且接近桩身的上部(尤其对于柔性桩)。当水平受荷桩土作用范围内竖向应力很小、水平应力起控制作用时,桩周土体的水平方向大主应力σ1不变,小主应力σ3的缩小对土体剪切摩尔圆的影响很小,因此,可以近似忽略竖向应力的不相似。根据土体的水平反力系数规律,可以控制选取模型桩的材料,从而使得模型的变形类型与原型相似。此类1g模型虽然不与原型完全相似,但也可以较好地反映原型桩的变形。
4 数值试验对比验证
前面分析得到通过选择适当的桩身材料,可以使得模型桩与原型变形特性相似。为了验证该分析结果,利用 ABAQUS有限元软件对这一类模型试验进行模拟,在理论上进一步验证水平受荷桩1g相似模型试验是否可行。计算中将桩视为弹性体且弹性模量为常量,土体本构选用Mohr-Coulomb弹塑性模型。数值模型试验计算参数如表2所示。原型水平受荷桩设定直径600 mm,入土深度10 m。模型桩的几何缩尺比λl为10,土体都为模拟砂土。砂土的弹性模量Es随深度正比例增加,根据砂土的状态和成桩类型,Es的增加比例系数ns取值不同。本研究ns取4 MPa/m,相当于中密砂中的打入桩[14]。砂土中埋置桩缩尺模型的桩材弹性模量应该按照λl缩小,模型土体采用原型土(参数相同)。数值计算模型的参数如表2所示。模型1代表桩与土都采用原型材料进行的普通室内缩尺试验,模型2代表桩身材料弹性模量按λE=λl缩尺后开展的缩尺试验。模型1和模型2的其他参数参照表1求得。

表2 数值模型试验计算参数表Table 2 Calculation parameters for numerical modeling experiments
考虑水平受荷桩的对称性,取一半建模。计算中采用八面体代替圆形截面进行网格划分,单元划分形式如图2所示。桩与土体都采用实体C3D8R单元,桩身共划分为640个单元,土体有18 200个单元。边界条件为:限制对称面除外的侧向边界的水平位移以及限制底部边界的竖向和水平向位移。水平加载分 3个阶段:由0加至100 kN,再从100 kN加至200 kN,再加至500 kN。
将缩尺模型1和2的计算结果通过相似关系反算其对应原型并与表2中的“原型”进行对比。图3所示分别为在100,200和500 kN水平力作用下的原型及对应模型反算的桩身水平位移。从图3可见:模型1与原型不相似且差别很大,所以,用原型桩材和原型土开展的缩尺模型试验去分析原型是不合理的;虽然模型2与原型结果有些差别,但总的规律很相似。为了进一步探索模型2与原型的相似程度,对比其桩身弯矩随深度的分布,如图4所示。从图3和图4可以看出:水平受荷桩模型试验的桩身模量按照几何相似比λl缩尺后,模型与原型基本相似。

图2 模型网格划分Fig.2 Model mesh generation
5 讨论

图3 不同水平荷载时原型与模型反算的桩身水平位移Fig.3 Lateral deflections of prototype pile and those extrapolated from model piles at different lateral loading levels

图4 桩身弯矩分布图Fig.4 Distribution of pile bending moment
水平受荷桩涉及桩土之间复杂的相互作用,通常意义上人们认为1g土工模型试验相似性较差,才发展了土工离心试验和其他类型的模型试验。其原因是土中应力状态与土体的性质相关,而1g模型中无法模拟原型土的应力状态。然而,1g桩基模型试验在国内外研究中仍然被广泛采用,原因是它的可控性、低成本和可重复性。Sedran等[3]得到竖向受荷桩1g试验不能满足相似的强制条件,但桩在主要承受水平荷载时与主要承受竖向荷载的工作机理不一样,最直接的体现为二者受力变形的控制方程不同。从相似的角度,不可能或者很难开展一个完全相似于原型的模型试验。工程中最为关心的是所开展的桩基模型试验能够与原型在变形或受力方面的相似关系较好即可,因此,实验设计都是针对主要影响因素入手。本文作者从桩身变形角度研究1g模型的相似关系,探索能否找到一种实际工程中容易实现水平受荷桩较好相似性的 1g模型试验方法。
前述理论和数值试验结果证实:水平受荷桩 1g模型桩采用弹性模量按原型桩模量 λl倍缩小的材料时,模型的变形特性大致与原型相似。不过,由图 3和图 4可以看出:桩身弹性模量按照 λl缩小后的 1g模型与原型相似性存在一定的误差。由1g模型试验反算原型桩时,桩顶位移反算值会小于实际值;桩身最大弯矩计算值也稍小于实际值;桩身最大弯矩点深度计算值比实际值稍小。这样,若对某工程桩进行模型试验,则在设计荷载下,当模型桩的最大桩身弯矩或最大位移达到或超过允许值时,可以推断实际桩基设计必然不能满足要求。

图5 桩身材料参数对水平受荷桩变形的影响Fig.5 Effects of pile material parameters on the deflection of laterally loaded piles
试验中,模型桩身材料的选择可以多种多样(铝管、有机玻璃、钢管和石膏等)。根据弹性模量的值来选取模型桩材会遇到一个问题,不同的材质重度以及泊松比不同。混凝土的重度约为24 kN/m3;铸铁和钢材的重度为60~80 kN/m3;而有机玻璃的重度为12~18 kN/m3;纯铜的重度约为87 kN/m3。钢材的泊松比为0.2~0.3,有机玻璃的泊松比为0.3~0.4,石膏的泊松比为0.17左右[15]。在前面原型桩数值试验的基础上,桩顶受到200 kN水平荷载、各参数不变而仅改变桩身自重γ或泊松比ν时,桩身水平位移沿深度的计算结果如图5所示。从图5可以看出:桩身自重改变或桩身材料泊松比的改变对水平受荷桩的变形影响较小。因此,通过选择缩小λl倍弹性模量选取桩材时,能够改进1g模型与原型的相似程度。
6 结论
(1)当缩尺模型试验采用与原型同种桩身材料及原型土时,几何尺寸的缩小将使得桩身的受力变形表现得更为刚性,缩尺模型与原型不相似。
(2)当模型桩材的弹性模量相似比等于几何相似比时,1g水平受荷桩模型与原型变形类型相似。可以用此类模型试验的结果根据相似关系近似反算原型的力学特性。
(3)采用 1g缩尺模型桩去模拟现场水平受荷桩时,模型结果反算所得的桩身水平位移和最大桩身弯矩都比实际偏小,最大弯矩点深度偏小。模型试验结果可用于推断或评价工程桩是否满足设计要求。
(4)模型桩材的选择多种多样,模型桩桩身重度和泊松比的改变对水平受荷桩受力变形影响不大,而桩材弹性模量是控制模型与原型变形相似的主要参数。
[1]Randolph M F,House A R.The complementary roles of physical and computational modelling[J].International Journal of Physical Modelling in Geotechnics,2001,1(1):1−8.
[2]曾友金,章为民,王年香,等.桩基模型试验研究现状[J].岩土力学,2003,24(增刊):674−680,686.ZENG You-jin,ZHANG Wei-min,WANG Nian-xiang,et al.Reviews of state-of-art modeling simulation on pile foundations[J].Rock and Soil Mechanics,2003,24(Suppl):674−680,686.
[3]Sedran G,Stolle D F E,Horvath R G.An investigation of scaling and dimensional analysis of axially loaded piles[J].Canadian Geotechnical Journal,2001,38(3):530−541.
[4]Franke E.Applicability of 1-g model tests in three cases[C]//Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering.Rotterdam,Netherlands:A.A.Balkema,1989:915−918.
[5]《桩基工程手册》编写委员会.桩基工程手册[M].北京:中国建筑工业出版社,1995:225−226.Editorial Committee of Pile Foundation Engineering Handbook.Pile foundation engineering handbook[M].Beijing:China Architecture and Building Press,1995:225−226.
[6]Tomlinson M J.Pile design and construction practice[M].London:Viewpoint Publications,1977:222−236.
[7]Poulos H G,Davis E H.Pile foundation analysis and design[M].New York:Wiley,1980:164−198.
[8]Meyerhof G G,Sastry V V R N,Yalcin A S.Lateral resistance and deflection of flexible piles[J].Canadian Geotechnical Journal,1988,25(3):511−521.
[9]Randolph M F.The response of flexible piles to lateral loading[J].Géotechnique,1981,31(2):247−259.
[10]吴恒立.计算推力桩的综合刚度原理和双参数法[M].2版.北京:人民交通出版社,2000:50−53.WU Heng-li.The composite stiffness principle and bi-parameter method for calculating laterally loaded piles[M].2nd ed.Beijing:China Communications Press,2000:50−53.
[11]Altaee A,Fellenius B H.Physical modeling in sand[J].Canadian Geotechnical Journal,1994,31(3):420−431.
[12]Floravante V.On the shaft friction modeling of non-displacement piles in sand[J].Soils and Foundations,2002,42(2):23−33.
[13]王馥廷,吴恒立.推力桩桩−土关系的模型律[J].重庆交通学院学报,1992,11(1):20−25.WANG Fu-ting,WU Heng-li.Model law of the relationship of laterally loaded pile and soil[J].Journal of Chongqing Jiaotong Institute,1992,11(1):20−25.
[14]胡德贵,罗书学,赵善锐.对桩周土弹性模量确定方法的探讨[J].西南交通大学学报,2001,36(1):23−26.HU De-gui,LUO Shu-xue,ZHAO Shan-rui.A determination method of soil shear modulus in pile foundation[J].Journal of Southwest Jiaotong University,2001,36(1):23−26.
[15]左东启.模型试验的理论和方法[M].北京:水利电力出版社,1984:242−249.ZUO Dong-qi.Theory and method of model test[M].Beijing:China Waterpower Press,1984:242−249.

