高等数学中矩阵典型案例探讨

徐 曙，薛志俊

（盐城纺织职业技术学院纺织工程系，江苏 盐城224005）

模块化教学模式，指以就业为导向，根据就业岗位的任职要求和在职业领域 （生涯）可持续发展的要求，建构教学体系，按认知规律和能力本位导向重构课程，形成模块化的课程体系，并在教学运行中，对教学方法、师资队伍建设、实习实训基地建设、考核考评等方面全面进行改革和创新的一种教学模式。

本文从几个典型案例出发，让学生知道为何而学，用在何处，充分调动学生求知欲，在培养学生的应用意识，提高学生应用线性代数的知识去分析和解决一些实际问题的能力等方面，与同行讨论。

1 加密问题

在军事通讯中，常将字符 （信号）与数字对应，如下图：

图1 字符与数字对应图

例如传输 “USA”对应一矩阵B＝（21 19 1），但如果按这种方式传输，则很容易被敌方破译，在军事或商业上都不可行，因此必须采取加密，即用一个约定的加密矩阵A乘以原矩阵B，传输矩阵为C＝AB′，收到信号的一方再将信号还原 （破译）为B′＝A－1C。如果敌方不知道加密矩阵，则很难破译.设收到的信号为C＝（20 41 －20）′，并已知加密矩阵为，问原矩阵B是什么？

编写MATLAB软件程序求B

＞＞syms A B；

＞＞A＝ [0 1 1；1 1 1；－1 0 1]；C＝ （20 41 －20）；

＞＞B＝inv（A）＊C′

即原信号为矩阵B＝ （21 19 1）。

太阳挂到中天了，红琴还在呼呼大睡。她仰面朝天，四肢伸展，睡得笔挺。薄薄的被子倒是缩成了一团，没有能盖住她窈窕的身躯，她的手足裸露在被子外面，富有曲线美的胸脯和小腹令人无限地遐想。随后，她的身子动了动，却没有醒来，像是梦魇了。他上前将薄被轻轻掖好，将她伸出被外的手脚盖住，没想到还是将她吵醒了，她极不耐烦地吼叫，干啥？他讪讪地道，你醒了？她突然对他产生了敌意，语气陡然变得很激愤，含着对他极大的不满，像机关枪似的滔滔不绝，嗔怪个没完没了。

2 条件优化问题[4]

工程师、经济学家、科学家和数学家常常要寻找一些特定集合内的X值，使得二次型XTAX取最大值或最小值。具有代表性的是，这类问题可以化为X是在一组单位向量中的优化问题。这类条件优化问题是很典型，在好多领域有广泛的运用。

求实函数f（x1，x2）＝ax21＋bx1x2＋cx22在满足x12＋x22＝1条件下的极值。我们有时利用微分法可以求得，但我们通常先找出二次型的矩阵，利用MATLAB中 [V，E]＝eig（）函数求出特征值和特征向量，正交矩阵化实对称矩阵为对角矩阵。

因此f（x1，x2）在单位圆上的极大值、极小值分别为A的最大、最小特征值。

3 人口迁移流动问题[5]

人口迁移流动，是人类社会发展的一个重要特征，同时也受经济社会发展诸多因素的影响。在中国，随着社会主义市场经济的发展，大量农村富余劳动力流入城市，改变了人口结构，促进了产业转型升级，加快了城镇化进程。设人口统计学的研究介绍某市每年有5%的城市人口移居农村，而15%的农村人口移居城市。假如某市年底城市人口为355万，农村人口为453万。忽略出生、死亡、移民等因素，假定城乡总人口保持不变，预测趋势便可为政府部门提供合理化建议。

n年后

利用MATLAB中 [V，E]＝eig（）函数就很容易地将这个差分方程对角化：

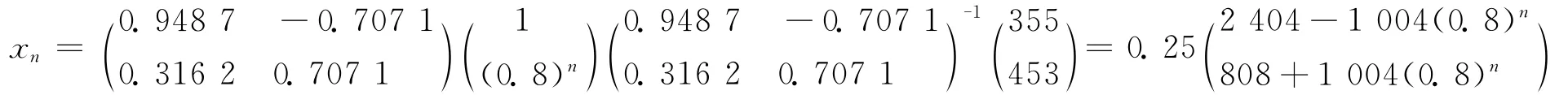
这些人口迁移选择的累积效果是不同区域的人口迁移的叠加。根椐极限原理，若干年后，城乡人口的比例为3∶1，趋于稳定。这种模型可以根椐实际情况及时修正，行政部门可以更合理地做好城市规划，让人口流动更合理。

4 二次通用旋转组合设计示例

在转杯纺纱工艺参数的配置中，转杯速度、分梳辊速度及捻系数是影响成纱质量最主要的工艺参数[6]。因此，需要寻求一个最佳的工艺参数组合，使成纱综合性能达到最优。

首先根椐表1的测试结果数据建立数学模型将问题化为求多元函数的极小值问题。将下表的数据以列向量形式存放至矩阵y。

表1 实验方案及测试结果

其次根椐二次通用旋转组合设计的要求，安排三因子二次通用旋转组合设计试验。为满足旋转性和通用性要求，取γ＝1.682。结构矩阵 （X）见表2。

表2 三因子二次通用旋转组合设计试验

第三，求解回归方程

（1）回归方程的模型

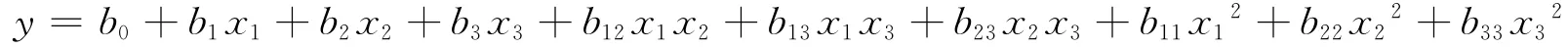
（2）利用公式b＝（X′X）－1（X′Y），求出回归系数。具体运算可以运用MATLAB软件。

教师在模块化教学中讲解完重要的知识点，可联系学生所学专业举一些应用实例，让学生在学习线性代数基本知识的同时，了解数学在本专业或生产实践中的应用，激发学生利用数学工具思考和解决专业或现实问题的求知欲，体现 “从实践中来，到实践中去”的模块化教学理念，感受解决实际问题成功的愉悦，非常有益于培养学生的数学素养，提高课堂教学效果。

[1]孙明辉，刘继来，王培，等.经管类学生高等数学学习现状调查研究——以河北北方学院为例 [J].河北北方学院学报：自然科学版，2011，25 （05）：98－104.

[2]薛志俊.《纺织应用数学》教材评价体系的探讨 [J].职业技术教育，2012，（04）：139－140.

[3]韩振芳，王宇红.高等数学教学改革探讨 [J].河北北方学院学报：自然科学版，2009，25（06）：77－79.

[4]李尚志.线性代数 [M].北京：高等教育出版社，2011：8.

[5]Lay DC.线性代数及其应用 [M].北京：电子工业出版社，2008：5.

[6]郁崇文.工程参数的最优化设计 [M].上海：东华大学出版社，2009：8.