在轨释放、分离载荷动力学仿真研究
舒 燕,李 志
(北京空间飞行器总体设计部,北京100094)
0 引言
某些航天器在飞行过程中需要完成对载荷的释放或分离任务,包括星箭分离、卫星的舱段分离和特殊有效载荷的释放、分离等[1]。载荷的释放、分离对航天器抗冲击性、姿态稳定性、快速姿态机动及稳定能力有很高的要求。大型载荷的释放、分离会对航天器平台造成较大冲击,并且分离前后航天器平台的质量、惯量以及质心位置都会发生较大的变化,给航天器平台的姿态控制带来困难。
针对此类载荷释放、分离问题,文章利用机械系统动力学仿真分析(Automatic Dynamic Analysis of Mechanical System,ADAMS)软件平台建立某载荷在轨释放、分离的动力学仿真模型,对其在轨释放、分离过程进行仿真研究,为载荷释放、分离方案设计提供参考。
1 在轨释放、分离载荷的特点
本文研究的载荷在轨释放、分离问题属于变结构、变质量、大干扰作用的多刚体动力学问题,具有以下几个典型的特点。
1)释放、分离的载荷为细长体构型,其体积、质量较大,内嵌于航天器平台,且安装位置偏离航天器几何中心,因此需考虑释放、分离过程中载荷与航天器平台的相互约束关系。
2)载荷释放、分离有方向和初速度要求,相比传统的星箭分离、舱段分离,载荷分离初速度较大(v≥2 m/s),因此要求分离机构能够提供较大的分离力。在载荷释放、分离的瞬间,机构动作将对航天器平台产生较大的干扰,而干扰力和力矩与释放、分离机构的特性和安装位置有关。此外,在载荷与平台之间存在运动耦合,需考虑其对释放、分离过程的影响。
3)由于载荷安装位置偏心,航天器释放、分离载荷后,其质量特性产生突变(平台质心偏移),需考虑质量特性变化对释放、分离过程的影响。
针对载荷在轨释放、分离问题,国内外已开展了许多相关研究[2-7]。这些研究的主要对象是沿中心轴线方向释放、分离的载荷,如飞船与运载火箭的相关分离[2,4-5];或者载荷虽然不安装于多体几何中心,但是呈对称分布,因此载荷的对称释放、分离不会造成分离后航天器平台的质心偏移[3]。而本文的研究对象是偏离于多体几何中心的释放、分离载荷,是一个质量特性发生较大变化的多体动力学问题。文章针对这类问题开展了相关仿真研究。
2 载荷在轨释放、分离的方案
本文研究的问题是利用机构从航天器舱内释放、分离载荷。载荷释放、分离主要过程包括:首先打开航天器舱门,启动锁紧/释放机构,执行载荷释放、分离操作;其次分离装置工作,推动载荷沿分离方向运动并达到所需分离速度;最终完成与航天器平台的分离。
根据载荷释放、分离方向以及分离机构[8]的不同,有三种典型的释放、分离方案:火工品轴向分离方案,弹簧轴向分离方案,弹簧侧向分离方案。轴向释放、分离的特点是分离行程较长,通常需要增加导向装置,但需开启的舱门角度较小;侧向释放、分离的特点是分离行程较短,但需开启的舱门角度较大。
1)火工品轴向分离方案
该方案采用具有连接、释放与分离功能的火工品锁作为释放、分离机构,如图1(a)所示,其壳体与航天器平台连接,连接杆与分离载荷连接。当起爆器工作时,引燃主装药,产生的高压气体作用于活塞;活塞推动解锁杆剪断剪切销并沿分离方向运动,使锁块落下,完成载荷释放;活塞继续运动,推动解锁杆、连接杆和载荷运动,实现载荷分离。方案中的导向机构采用导轨、滑轮方案,导轨与航天器平台连接,滑轮配置在载荷上。
2)弹簧轴向分离方案
该方案的释放机构采用具有连接、释放功能的爆炸螺栓或火工品锁,其分离机构采用弹簧分离推杆,由弹簧和内、外套筒组成,如图1(b)所示。外套筒与航天器平台固连,端面设置限位卡环,防止分离时弹簧和内套筒被弹出外筒,并使弹簧工作在线性程度较好的区段;内筒外表面涂敷了固体润滑膜,分离时,内套筒在弹簧力作用下向外滑动实现分离。其导向机构同火工品轴向分离方案。
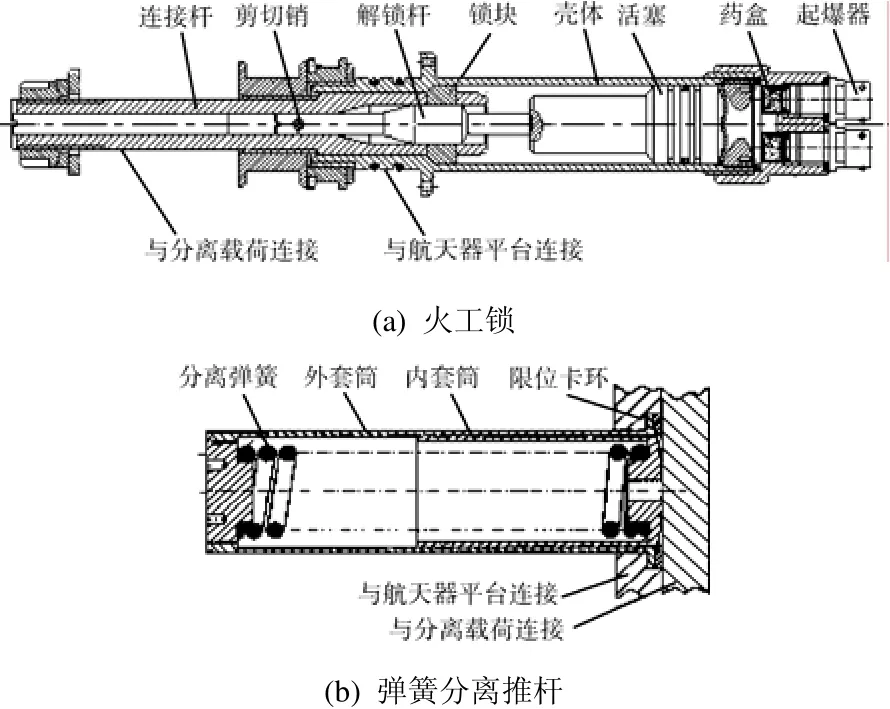
图1 分离机构示意图Fig. 1 Schematic diagram of two separation mechanisms
3)弹簧侧向分离方案:与弹簧轴向分离方案类似,只是其分离方向为侧向。
3 在轨释放、分离载荷动力学仿真分析
载荷在轨释放、分离的仿真研究选用ADAMS作为软件平台,通过虚拟样机建模实现载荷释放、分离的动力学和运动学仿真分析[9-10]。
3.1 仿真模型及参数
针对载荷在轨释放、分离机构的系统需要在ADAMS平台上建立相关模型,主要包括航天器平台模型,载荷模型,释放、分离机构模型。对于轴向释放、分离方案,还须建立导向机构模型。系统仿真模型单元及其大致约束关系如图2所示。

图2 系统仿真模型组成框图Fig. 2 System elements of the simulation model
1)航天器平台模型和载荷模型
将航天器平台和载荷视为刚体来建模,相关参数包括质量、质心位置和惯量。基准坐标系设定为Os-XsYsZs,平台与载荷在YsOZs面投影位置关系如图3所示,平台质心Oc的坐标为 (Xc, Yc, Zc),载荷质心Op的坐标(Xp, Yp, Zp)。轴向释放、分离是指载荷沿 Xp轴方向分离,侧向释放、分离指载荷沿OsOp连线在YsOZs面内投影方向分离。

图3 平台、载荷位置关系示意图Fig. 3 Relative positions of the platform and the payload
2)分离机构模型及分离力
依据图 1所建立的弹簧分离推杆和火工品锁的ADAMS模型,其弹簧分离力和火工品分离力按照分离速度2 m/s的要求选取,如图4所示。

图4 分离力曲线图Fig. 4 The separation force curve
3)导向机构模型
针对轴向释放的较长分离行程,采用了图5所示楔形导轨、滑轮模型来约束载荷分离方向的运动,同时在横向上还可对载荷起到一定的约束作用。导轨配置在航天器平台上,滑轮配置在载荷上。导轨与滑轮之间存在运动学上的约束关系,使载荷沿预定的方向释放。在ADAMS模型中通过定义连续接触力来实现约束。

图5 导轨、滑轮模型图Fig. 5 Models of the slide rail and the pulley
导轨、滑轮间的正压力采用冲击函数法计算,它由两部分组成:一是两个构件之间相互切入而产生的弹性力,二是相对速度产生的阻尼力。系统的力学模型可定义为一种非线性弹簧,则正压力为

式中: C为弹簧阻尼;K为弹簧刚度;r为弹簧两端距离;S为弹簧行程;P为弹簧预载荷。
导轨、滑轮间非线性摩擦力可用库仑模型计算,则有

式中:N为法线方向压力;μ为摩擦因数。

式中:v是滑动速度;sv是静滑移速度;dv是动滑移速度;sμ是静摩擦因数;dμ是动摩擦因数。这些参数一般与构件的材质、加工方法、工况等因素有关,模型中选择系统默认值。
3.2 仿真分析
针对上述三种载荷释放、分离方案,分别开展了动力学仿真分析。3种方案的仿真结果见表1。

表1 3种分离方案仿真数据对比Table 1 Simulation data of three separation schemes
通过对比弹簧轴向分离与弹簧侧向分离方案的仿真数据可以看出:在达到相近分离速度的情况下,弹簧侧向分离机构对航天器平台的扰动较大。其原因之一是侧向分离的行程较短,载荷在较短的时间内脱离平台,使平台的惯量在很短时间内大幅减小;之二是侧向干扰力矩相对较大。
通过对比火工品轴向分离与弹簧轴向分离方案的仿真数据可以看到:在达到相近分离速度的情况下,若平台姿态无控制,则两种分离机构执行分离对平台姿态的影响接近;火工品分离的作用力作用时间较短而其幅值较大,弹簧分离的作用力时间较长而幅值较小,因此火工品分离机构对载荷的冲击较大。
针对载荷释放、分离的研究结果,文章选择了弹簧轴向分离方案。因为在相同分离速度要求下,这种方案中的载荷所受到的冲击小,对平台的姿态干扰也小。
3.3 仿真优化
针对选定的弹簧轴向分离方案进行仿真优化。在保证分离速度的前提下,为了进一步减小分离机构动作对平台的干扰,对方案中的导向机构进行了改进设计——即增加一组滑轮(如图6虚框中对应的第2滑轮组)。当图6中第2组滑轮与第1组滑轮的距离L按照最小安装间距(60 mm)取值时,则载荷释放时俯仰角速度由5.33 (°)/s减为3.09 (°)/s,偏航角速度由 3.28( °)/s减为 2.18( °)/s,角速度对比曲线如图7。因此,增加滑轮组可以减小载荷离开平台时相对平台的角速度。

图6 改进的导向机构图Fig. 6 Improvement of the slide rail and pulley mechanism
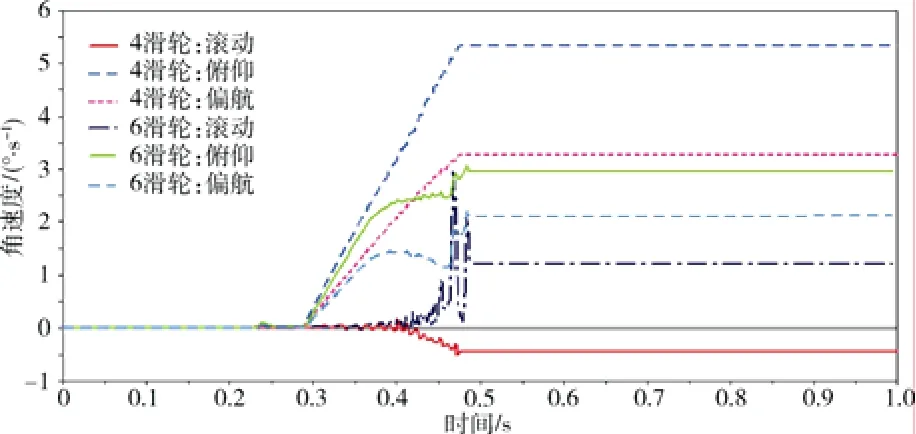
图7 导向机构方案改进前后角速度仿真结果对比图Fig. 7 The comparison of simulation results of angular velocity before and after improvement of the guiding mechanism
为进一步分析第2组滑轮与第1组滑轮的间距对载荷释放分离的影响,以间距L为变量,选取载荷相对平台角速度为目标进行参数优化仿真分析,结果如图8所示。由图8曲线可知:当L位于0.06~0.11 m之间时,随着L值增加,第3组滑轮离开平台时载荷相对角速度以及载荷与平台完全分离时刻(第 1组滑轮离开平台)的相对角速度呈减小趋势;当L位于0.11~0.16 m之间时,随着L值增加,第3组滑轮离开平台时载荷相对角速度呈减小趋势,而载荷与平台完全分离时刻的相对角速度呈增加趋势,且前者相对角速度小于后者。通过仿真分析得到:当L=0.11 m时,载荷与平台完全分离时刻的相对角速度最小,其俯仰角速度为 2.17( °)/s,偏航角速度为 1.19( °)/s,滚动角速度为 1.09( °)/s。

图8 载荷相对平台姿态角速度曲线Fig. 8 Relative angular velocity of the payload with respect to the platform
4 结论
通过对航天器在轨释放、分离载荷的动力学仿真研究,获得结论如下:
1)通过对三种释放、分离方案的仿真研究及仿真结果对比,认为弹簧轴向分离方案最适用于载荷在轨释放、分离,因为采用这种方案时在相同分离速度要求下,载荷所受到的冲击小,对平台的姿态干扰也小。
2)通过对载荷轴向释放方案中的导向机构改进设计——增加一组滑轮(第2滑轮组),可以大大地减小载荷分离时相对平台的角速度,且将第1滑轮组与第2滑轮组之间的距离L增加至0.11 m时,载荷分离时相对平台角速度最小。
(References)
[1]Fosness E R, Buckley S J, Gammill W F. Deployment and release device efforts at the Air Force Research Laboratory Space Vehicles Directorate[C]//AIAA Space 2001 Conference and Exposition. Albuquerque, NM,2001: 1-6
[2]李中郢, 崔乃刚. 载人飞船与运载火箭分离过程的仿真研究[J]. 哈尔滨工业大学学报, 1999, 31(1): 119-122 Li Zhongying, Cui Naigang. Simulation study of separation process between manned spacecraft and launch vehicle[J]. Journal of Harbin Institute of Technology, 1999, 31(1): 119-122
[3]张兵, 岑拯. 多星分离的 ADAMS仿真[J]. 导弹与航天运载技术, 2004(2): 1-6 Zhang Bing, Cen Zheng. ADAMS simulation of many satellites separation[J]. Missile and Launch Vehicle Technology, 2004(2): 1-6
[4]朱仁璋, 汤溢, 李颐黎, 等. 神舟飞船逃逸救生分离动力学分析[J]. 航天器工程, 2004, 13(1): 132-140 Zhu Renzhang, Tang Yi, Li Yili, et al. Dynamic analysis of escape rocket separation with manned spacecraft[J].Spacecraft Engineering, 2004, 13(1): 132-140
[5]肖业伦, 李晨光. 飞船舱段应急分离过程的动力学分析和计算[J]. 中国空间科学技术, 2005, 8(4): 25-30 Xiao Yelun, Li Chen’guang. Dynamic analysis and computation of emergency separation of manned spacecraft module[J]. Chinese Space Science and Technology, 2005, 8(4): 25-30
[6]Kindt D H. Cassini/Huygens: a challenge in international interface design, integration, and cooperation[C]//Proceedings of SPIE - Cassini/Huygens: A Mission to the Saturnian Systems, 2803_002: 10-21
[7]Herlach U R, Tatalias P, Schmid B, et al. Huygens separation mechanisms[C]//Proceedings of the Sixth European Space Mechanisms & Tribology Symposium.Technopark, Zürich, Switzerland, 1995-10-04
[8]陈烈民. 航天器结构与机构[M]. 北京: 中国科学技术出版社, 2005
[9]李增刚. ADAMS入门详解与实例[M]. 北京: 国防工业出版社, 2007
[10]王国强, 张进平, 马若丁. 虚拟样机技术及其在ADAMS上的实践[M]. 西安: 西北工业大学出版社, 2002

