CPⅢ高程网最小独立闭合环的一种搜索算法

李建平，明祖涛，张 届，游振兴

（中国地质大学（武汉）信息工程学院，湖北武汉430074）

CPⅢ高程网最小独立闭合环的一种搜索算法

李建平，明祖涛，张 届，游振兴

（中国地质大学（武汉）信息工程学院，湖北武汉430074）

水准测量结束后，对观测成果进行往返较差、附合路线及闭合环的闭合差检查是必不可少的工作。CPⅢ高程控制网网形独特，它部分边含有往返测或双次观测且属于大型控制网（观测边可能含有数千条）。根据最小独立闭合环及最小独立附合路线的限制条件，依据CPⅢ高程控制网的特点，利用Dijkstra算法思想，提出了最小路径搜索法并进行编程实现，通过算例验证了其正确性和高效性。

最小独立闭合环；最小独立附合路线；最小路径搜索法；闭合差

水准测量外业数据采集完成后，有可能观测结果不符合限差要求，甚至会有粗差混入其中，影响平差成果的正确性和可靠性，且相关规范也要求进行每km水准测量高差全中误差的计算，这就要求对水准网进行各种闭合差计算。对于小型简单的水准控制网而言，可以人工检查闭合差，但在控制网较复杂或网形很大时，如果采用人工计算，不但计算量大，而且极容易出现2类错误：一是闭合环或附合路线找不完全；二是所找闭合环间或附合路线间存在相关关系[1]。为避免人工计算的繁琐和易出现的错误，利用计算机进行最小独立闭合环及最小独立附合路线的自动搜索是最好的方式。目前，已经有多种有益的最小独立闭合环的搜索算法。文献 [2]采用图论的方法来进行闭合环的搜索，算法结构复杂，需要具备很好的数据结构知识，且主要针对平面控制网，未能充分考虑水准网的各种情况，如CPⅢ高程控制网是单程矩形闭合环，部分边有往返测。文献[3]探讨了3种闭合环搜索算法：基于邻接矩阵变换的方法、基于生成树和余树变换的方法、基于深度优先搜索的方法。第1种方法只能搜索独立闭合环，后 2种搜索到的是长度最短的独立闭合环，不一定边数最少。文献 [4]中基于迭代加深搜索的算法不稳定，有时无法搜索所有的闭合环。而对于最小独立附合路线，以往文献则较少研究，部分算法也只是能搜索出独立附合路线,如文献 [5]中基于最小生成树的算法，有些控制网对附合路线的长度也有要求，如CPⅢ高程控制网精密水准测量要求附合路线长度不大于3 km，所以搜索最小独立附合路线仍具有较大意义。本文根据最小独立闭合环及最小独立附合路线的特点，利用Dijkstra算法思想，讨论了最小路径搜索法，并通过编程实现。

1 最小路径搜索法思想

1）最小独立闭合环和附合路线的条件及个数的确定。

对于水准网而言，设观测边（即观测高差）个数为 gd，其中有往返观测或双次观测的独立边个数为sgd，已知点个数为yd，未知点个数为wd。最小独立闭合环应满足如下条件[6]：

①所有闭合环应该是相互独立的（线性无关），即任何一个闭合环都不能由其他闭合环线性合成。满足独立性的要求既可避免重复计算，也可以避免遗漏，一般而言，水准网的独立闭合环个数为：

②闭合环所包含的边数最少，这样可以提高检测粗差的能力。

③对应边数相同的闭合环，应取长度最短的环。

对于最小独立附合路线，也应满足上述3个条件，水准网的独立附合路线个数为：f=yd 1。显然，需要计算往返较差或双次同向观测较差的观测路线个数为：w=sgd。

那么，往返较差或双次同向较差、独立闭合环、独立附合路线的总个数为：

这正好等于条件平差时条件方程式的个数。如图1所示，A,C,F为已知点，其余点为未知点，观测高差个数为gd=20,有往返测或双次同向观测的观测边个数为sgd=4，已知点个数为yd=3，未知点个数为wd=8。则独立闭合环个数为b=(gd sgd)(yd+wd)+1=6，独立附合路线个数为f=yd 1=2，往返观测或双次同向观测路线个数为 w=sgd=4，总共需要计算的闭合差个数为b+f+w=gd w d=12。

图1 水准网图

2）闭合环与附合路线的相互转化。水准测量中，观测路线实测高差与理论高差经常不相符合，形成闭合差，具体可分为往返较差（或双次同向观测较差），环线闭合差和附合路线闭合差。设 k1、k2为2个已知点，高程值分别为H1、H2,有1组观测高差h1、h2、h3、…、hn。

若h1、h2的起点、终点相反（或相同），则往返较差（或双次同向观测较差）为：fh=±h1±h2；

若h1、h2、h3、…、hn起闭于k1点，则环线闭合差公式为：fh=±h1±h2±h3±…±hn；

若h1、h2、h3、…、hn起始于k1点，终止于k2点，则附合路线闭合差公式为：

式中，正负号取决于观测路线的方向。由环线闭合差公式和附合路线闭合差公式可以看出，两者有些类似，事实上，两者可以相互转化。如图1所示，有路线A→B→C，其中A、C为已知点，B为未知点，设A、C的高程分别为HA、HC,则附合路线闭合差为fh=h1+h2（HCHA）。

若在A、C之间增加1条虚拟观测值hAC，并令hAC= HCHA,方向为A→C，A、C之间的距离设为SAC=0,C点变为未知点；则闭合路线A→B→C→A的环线闭合差公式为fh=h1+h2hAC=h1+h2（HCHA）。对于整个水准网，未知点个数增加1，已知点个数减少1，独立闭合环增加1，独立附合路线减少1，观测高差个数增加1，则总共需要计算的闭合差个数为 gd wd=12，保持不变。若重复下去，使水准网已知点个数减少到1个，则整个网只需计算环线闭合差及往返较差。

同理，闭合环也可以转化为附合路线。如图 1所示，闭合环A→J→B→A中，闭合差为fh=-h1+h4h8,令A、B高程分别为HA，HB=h1+HA，则h1=HBHA,删除高差 h1，则A→B的附和路线闭合差为fh=-h8+h4（HBHA）=-h8+h4h，如此，整个水准网，未知点个数减少1，已知点个数增加1，独立闭合环个数减少1，独立附合路线个数增加1，需要计算的闭合差总数不变。

由以上可以看出，附合路线和闭合环联系紧密，相同之处是都要搜索最小路径（边数最少，长度最短），这使得设计算法时可以一起考虑。

3）最小路径搜索法。为记录水准网中闭合环或附合路线搜索的路径，需用“邻接点”来表示，这里的邻接点不同于数据结构中的邻接点。如图 1所示，以A点作为源目标点，寻找其他点到A点的最小路径（边数最少，距离最短）。网中B、J、H、I与A点直接相连，其余点没有与A点直接相连，它们必须借助其他点才能与目标点联系。如果一个点借助另一个点与目标点发生了联系，称另一个点是这个点的“邻接点”[7]，如C点借助B点与A点发生了联系，则C点的邻接点为B。而B点的邻接点为A，可以理解为B点通过A点与A点发生了联系；同理A点的邻接点为A。

根据最小独立闭合环和最小独立附合路线的条件，邻接点也应该唯一确定。例如，K点的邻接点可以是B,也可以是J,则先判断B，J到A点的边数，边数少的为K点的邻接点。若边数相同则判断K→B→A与K→J→A的距离，距离短的为K的邻接点。如此，一般情况下便可唯一确定邻接点。

综上所述，最小路径搜索法可利用邻接点标记搜索路径，利用 Dijkstra算法思想，设目标点点号为 k,搜索各点到k点的最小路径的具体计算流程如下：

①开辟3个数组：名为neighbor的数组，记录每点的邻接点号；名为edgen的数组，记录每点到目标点边的个数；名为S的数组，记录每点到目标点的距离。其中neighbor（k）=k，edgen（k）=0，S(k)=0，其余各点neighbor数组的值为-1（表示没有邻接点），edgen数组和S数组值为100000（表示边数和距离无穷大）。

②依次访问每一个高差观测值（若该观测边含有往返观测或双次同向观测，则与当前路线方向相反的高差观测值或双次同向观测值中距离较长者不参与最小路径搜索），记录后视点号（设为 p1）和前视点号（设为p2），两点间的距离为s12，根据p1点和p2点到目标点k的边数e1和e2以及距离s1和s2，判断p1是否可以作为p2的邻接点以及p2是否可以作为p1的邻接点。p1可以作为p2的邻接点的条件是

p2可以作为p1的邻接点的条件是

若 (1)式成立，则neighbor(p2)=p1，S(p2)=S (p1)+s12，edgen(p2)=edgen(p1)+1；若 (2)式成立，则neighbor(p1)=p2，S(p1)=S(p2)+s12，edgen(p1) =edgen(p2)+1。

③一般情况下，依次访问每一个观测值之后一些点到目标点不是最小路径，有些点还没有找到邻接点，这时需要重复步骤②，直到所有观测高差均不再满足式(1)及式 (2)，这时各点到目标点的最小路径搜索完成。

依据上述方法，可在计算机上编写最小路径搜索函数，为方便论述，设函数名为FindM inPath。

2 最小独立闭合环及最小独立附合路线的搜索

搜索最小独立闭合环和最小独立附合路线之前，应先进行观测高差的往返较差检查或双次同向观测高差较差检查，并对有往返观测的边和双次同向观测的边进行标记。

对于最小独立附合路线，搜索过程如下：

1）已知点个数为 yd，已知点号依次为 0、1、2、…、yd 1。建立一个双重循环，依次选取已知点i=0、1、2、…、yd 2。选取某一已知点 i后，调用最小路径搜索函数FindM inPath，搜索出任意其他点到i点的最小路径。判断剩余的点j=i+1，i+2，…，yd 1中到i点边数最少，距离最短的点。设此点点号为 imin，则搜索出了一条最小路径的附合路线，即从已知点i，经过若干未知点到达已知点imin。

2）选取已知点i的下一个点，令i=i+1，继续调用最小路径搜索函数FindM inPath，在剩余的已知点中找到离i点边数最少，距离最短的点，此时又搜索出一条最小路径的附和路线；继续选取下一已知点，令i=i+1；如此继续直到已知点 i=yd 2（包括此点），则共搜索出yd 1条最小独立附合路线，搜索完毕。

如图1所示，A→J→B→A为一条最小闭合环。最小闭合环搜索思路为：删除高差h1，搜索A到B点的最小路径，类似于搜索最小附和路线。易知最小路径为A→J→B,与h1合并后即得到最小闭合环A→J→B→A。最小独立闭合环的具体搜索过程为：

1）观测高差个数为gd，各观测高差序号为0、1、2、…、gd 1，依次遍历各观测高差。设选取观测高差的序号为i=0，以前视点为目标点调用最小路径搜索函数 FindM inPath，搜索出后视点到前视点的最小路径，其中不参与搜索最小路径的观测高差序号为i。这样搜索出了包括观测高差i的最小闭合环。为保证最小闭合环是独立的，对搜索出的最小闭合环各个观测高差都标记为已经使用。

2）选择下一个观测高差，令 i=i+1。若这个观测高差是双次同向观测高差中距离较长者或已经使用，则继续选择下一个观测高差，否则以前视点为目标点调用最小路径搜索函数 FindM inPath，限制条件与 1)中相同。若现在的观测高差是往返观测边中的一个且最小路径方向与当前观测高差异向，则退出，继续选择下一个观测高差，否则此时就搜索到了包含观测高差i的最小闭合环，如此下去直到遍历各个观测高差。最终搜索到的最小独立闭合环的个数为b=水准网边数-水准网点数+1。

3 算例分析

上面原理已经用VisualBasic平台编程实现，且已经应用于大量算例进行验证。水准网数据格式采用科傻 in1标准格式，读入观测文件后自动计算已知点个数、未知点个数、观测高差个数等。读入图1中的水准网数据后界面如图2所示。

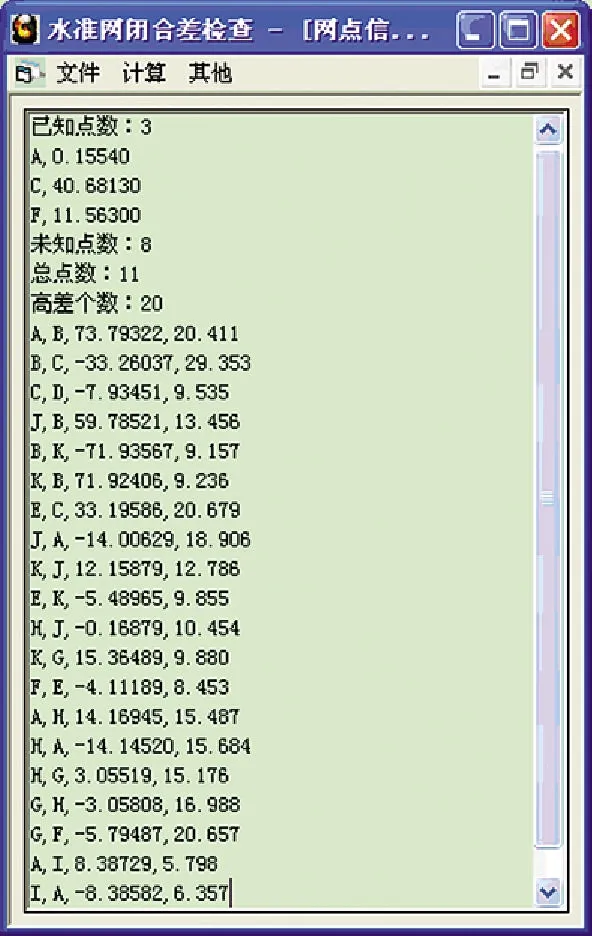
图2 水准网闭合差检查界面

由图1可知，水准网往返较差个数为4，独立闭合环个数为6，独立附合环个数为2，利用上述方法解算结果如表1所示。

表1 水准网往返较差、最小独立闭合环、最小独立附合路线结果/mm

由表1可知，搜索的闭合环和附合路线个数均正确，且均是最小独立闭合环或附合路线，其中附合路线F→E→C，往返较差A→H以及闭合环F→G→K→E→F闭合差超限。附合路线F→E→C和闭合环F→G→K→E→F有1条公共边F-E，推断F→E可能超限，由闭合环B→K→E→C→B闭合差没有超限可判断边E→D观测值是合格的，故推断F→E超限，需重测。闭合环H→A→J→H闭合差合格，说明各边均合格，而A→H的往返较差超限，说明观测边A-H中的距离较长的观测高差不合格，查看观测文件后判断出 H→A观测高差超限，需重测。

又如，实测了某高速铁路CPⅢ高程控制网，网形如图3所示，网的长度大约为20 km，其中观测高差个数为1 414，有往返测的边个数为363，已知点个数为21，未知点个数为688，用前面所述的方法成功搜索出了20条最小独立附合路线，363条往返路线和343条最小独立闭合环，以精密工程测量要求设置限差，结果全部合格，不需重测。

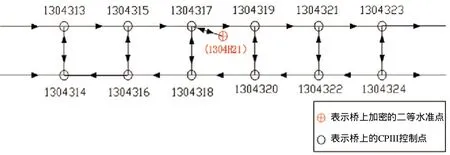
图3 CPⅢ高程控制网示意图

4 结 语

本文所提出的算法不仅简单易懂，而且只需已知点信息和观测值信息即可编程实现，无需其他附加信息，自动化程度高。根据闭合环和附合路线的特点，将两者结合起来，不仅搜索出最小独立闭合环，而且完整正确地搜索出最小独立附合路线，最大限度地探测粗差并评定观测结果的质量。而且顾及到了CPⅢ高程控制网部分边有往返测的特点，搜索闭合环和附合路线更科学，更易检测粗差。另外，根据CPⅢ高程控制网的实例，观测高差个数为1414个时搜索闭合环和附合路线只需10 s左右，说明此方法搜索速度较快。解算出的往返较差、最小闭合环和最小附合路线相互独立，包含条件平差的所有信息，且使得系数矩阵最大程度的成为稀疏矩阵，可依此列立条件方程式进行平差，提高水准网的解题容量和速度。最后，本文所提出的方法原理也完全适用于GPS网，对平面网的角度闭合差、距离闭合差等的计算也有借鉴意义。

[1] 马文静，刘成龙.自动计算水准网中闭合差的图论解决方法及应用[J].铁道勘察,2006（2）：10-11

[2] 冯琰,张正禄,罗年学.最小独立闭合环与附合导线的自动生成算法[J].武汉测绘科技大学学报,1998,23(3):255-258

[3] 赵一晗,伍吉仓.控制网闭合环搜索算法的探讨[J].铁道勘察,2006(3):12-14

[4] 邹进贵，冯晨.控制网最小独立闭合环搜索算法研究[J].地理空间信息,2008,6(6):97-99

[5] 刘晓云,张世娟,胡秀珍.水准网闭合环自动生成技术的研究[J].测绘技术装备,2010,12(1):3-5

[6] 姚连壁,周小平.基于MATLAB的控制网平差程序设计[M].上海:同济大学出版社,2006

[7] 宋力杰.测量平差程序设计[M].北京:国防工业出版社,2009

Searching Algorithm of the Independence Minimal Closed Loop in CPⅢElevation Control Net

by LI Jianping

After the end of leveling survey,misclosure checking about the observed results of round trip difference,annexed line,closed loop is essential.CPⅢvertical control network form a unique network,part of its edges contain round trip measured and double observations,and it is a large control network(the observation side may contain thousands).According to the constraints of the smallest independent closed loop and the smallest independent annexed line,takinginto account the characteristics of the CPⅢvertical control network,and using the idea of the Dijkstra algorithm,this paper proposed the minimum path search method and achieved it by writing a program.In this paper,an example proved its correctness and efficiency.

minimum independent closed loop，minimum independent annexed routes，minimum path search method，misclosure

2012-07-12

P224

B

1672-4623(2012)06-0150-04

李建平，硕士，研究方向为大地测量学与测量工程。