快速货车制动盘热应力分析＊

张新芳，李 芾，孙树磊，李受钊

（西南交通大学 机车车辆系，四川成都610031）

随着世界经济的发展和科技的进步，各国铁路与公路、航空、海运等运输行业之间的竞争愈加激烈。铁路运输以其运量大、速度快、安全、节能和对环境污染小等优势成为人类重要的交通运输方式。为了减少客货列车的速度差，且市场也迫切需要铁路提供集装箱、小汽车、冷藏等货物快运的服务，因此铁路货运提速势在必行，但随着速度的提高，制动时热负荷将急剧增加，传统的踏面制动已经不能满足制动要求。盘形制动具有功率大、摩擦系数稳定及可减小车轮踏面磨耗等特点，故在速度高于140km／h的货车转向架上普遍采用盘形制动。图1为意大利FIAT快速货车转向架，其最大商业运行速度为140km／h，基础制动装置采用轴盘制动，每轴安装两套盘形制动单元。

关于客车盘形制动热负荷的问题，国内外对其均进行了相关的研究。如近年来国内吴萌岭［1-2］研究了准高速客车制动盘的温度场及应力场问题，提出摩擦盘圆周方向上的边界条件和约束条件都一致的假设，将三维模型简化为二维轴对称问题处理；王文静等［3-6］在制动盘分析中也进行了轴对称假设，取制动盘的一个对称角作为分析对象，虽然较二维模型的计算方法有一定改进，但未考虑制动阻力，且假定材料的性能不随温度变化。

快速货车由于其轴重大，速度快，对制动盘的要求更加苛刻。本文对国内开发的160km／h快速货车进行了制动计算，并对制动盘进行了设计及选材，利用ANSYS建立有限元模型并进行制动盘温度场及应力场的计算。

图1 FIAT快速货车转向架

1 制动盘选材

货车制动时，会对制动盘产生巨大的制动热负荷和热冲击，并由此产生较高的温度梯度和热应力。因此制动盘必须选用性能优良的材料。蠕墨铸铁制动盘和金属基合成闸片是比较合理的选择［7］。蠕墨铸铁热膨胀系数小，在常温及高温下机械性能较好，热传导系数较高，并且铸造性能良好，易于工艺优化和批量生产，其与半金属基合成闸片相匹配的摩擦副，机构合理，摩擦系数稳定，可以很好的满足制动要求。本文所用蠕墨铸铁（RuT380）的主要力学性能见表1。制动盘相关尺寸参照我国现有的制动盘确定，见表2。

表1 蠕墨铸铁主要力学性能

表2 制动盘设计尺寸

2 边界条件

2.1 初始条件

本文利用ANSYS计算速度160km／h，轴重17t的快速货车在一次紧急制动过程中的热应力分布。通过制动计算，列车制动距离为1 076m，制动时间47s，平均减速度为0.97m／s2，考虑到在潮湿轨面上高速运行时黏着系数下降以及有效制动距离的限制条件，制动过程采用两阶压力，压力转换点为130km／h，即从160～130km／h，单位制动力b=87N／kN，从130km／h至停车，b=100N／kN。

2.2 热流密度

热流密度是指单位时间单位面积上输入的热量。制动过程中，制动盘将列车的动能转化为热能，ANSYS中将热能以热流密度的方式加载到制动盘摩擦环上。

任意时刻动能的减小量Q为：

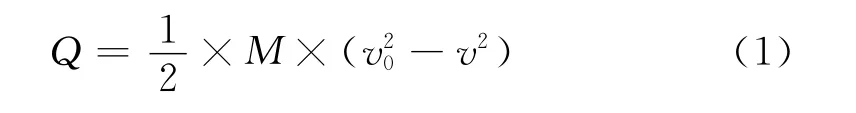
式中M为轴重（kg）；v0为各速度区间制动初速（m／s）；v为列车任意时刻的行驶速度（m／s）。

由于制动盘与闸片的比热、密度、导热系数的不同，热量分配存在一个系数，材料的属性随温度的变化也会有一定的变化，因此该系数的确定将受到诸多因素的影响。根据相关研究，其取值一般为0.85或0.9，本文中取0.9。各速度区间内制动盘吸收的能量Qd：

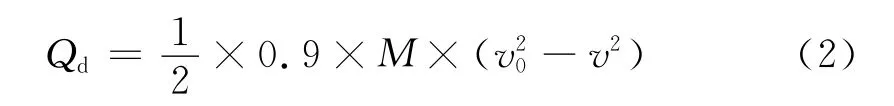
将热量Qd对时间t求导，再除以摩擦面积即可得各速度区间任意时刻热流密度函数为：

式中A为制动盘每侧参与摩擦的面积（m2）；n为参与摩擦面数。

这样输入制动盘的热流密度的函数就可以写成：

上述公式中的各速度区段的加速度a及对应的时间t是根据《列车牵引计算》相关公式计算得到。由此即可求得制动盘各时间点上的热流密度值，如图2所示。其中9.6～12.5s时，热流密度上升，是由于从130～120km／h速度区间，单位制动力从87N／kN增加至100N／kN，使减速度增加所致。

2.3 对流换热系数

运动流体和温度不同的固体表面间所进行的热量传递过程称为对流换热。制动盘的对流散热分为两个过程［8］：在制动过程中，制动盘散热处于空气受迫对流散热状态；制动结束后，制动盘散热处于自然对流散热状态。由于自然对流相对于强迫对流很小，且在制动结束后温度和应力都逐渐下降，可忽略自然对流。

图2 热流密度随时间变化的关系

空气在掠过盘面过程中会发生层流、紊流的转变。

（1）层流。

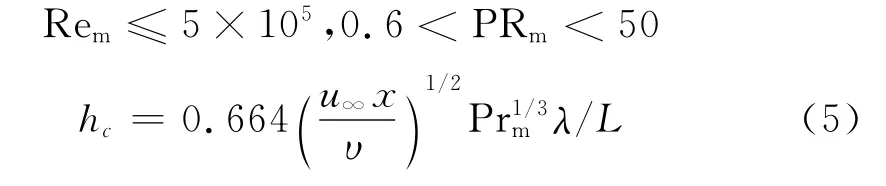
式中Rem为雷诺数；Pγm为普朗特数；hc为对流传热系数（W／（m2·K））；u∞为来流速度（m／s）；x为空气距板前端的距离（m）；L为制动盘表面的尺寸（m）；υ为空气运动黏滞系数（m2／s）；λ为制动盘的热传导率（W／（m·K））。

（2）紊流。5×105＜Rem≤108，0.6＜Prm＜60

（3）混合边界层

气流通过制动盘外侧面的模型采用横掠单管模型。其Rem数为：

式中d0为圆柱的外径（m）。

制动盘的运动是车轮随列车的平动加制动盘自身的旋转，故盘面上来流速度u∞是列车行驶速度v与制动盘自转切向速度vτ的几何合成，v与vτ相互垂直，得到u∞为：

式中ω为制动盘转动角速度（rad／s）；r为制动盘外圆半径（m）。

其特征关联式为：

式中c、n为常数，可通过查表得到。

散热筋板间的几何结构复杂，空气流速难以精确计算，所以取列车速度近似模拟空气流速u∞。

其特征关联式为：

式中m，k，p为常数，可通过查表获得；s1，s2为与散热筋排列方式有关的常数；Prf，Prw为制动盘附近空气与盘面温度的平均温度下的普朗特数及空气温度下的普朗特数。由以上公式、相应的普朗特数、雷诺数计算公式及制动盘尺寸即可确定随时间变化的对流换热系数h，如图3所示。

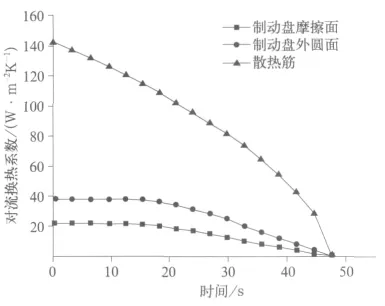
图3 对流换热系数随时间的变化关系

3 制动盘有限元建模及结果分析

采用有限元法分析制动盘在一次制动过程中温度和应力的变化情况。为简化计算，采取如下假设：（1）由于列车速度很高，将热源和闸片压力均匀分布在摩擦面上。（2）闸片和盘接触为面与面接触，不考虑其表面的粗糙度，且忽略制动过程中接触面的磨损；（3）制动初始温度为室温（293K），不考虑外界温度变化；（4）材料只有弹性变形。

考虑到盘体结构及热载荷的对称性，建立圆周方向1／6循环对称有限元模型进行瞬态热分析。摩擦环与散热筋的过渡处采用solid 87单元过渡连接，其余部分采用solid 70单元。在制动盘摩擦表面采用表面效应单元SURF152单元，以同时施加热流密度和对流换热系数。热分析中盘面与闸片的制动力作用以等效热流密度方式考虑，故在网格划分中不包括闸片部分。建立的有限元模型如图4所示。

热流密度及对流换热系数通过表格的形式加载，输入材料相关参数，进行热分析。结果表明，每轴安装两个制动盘时，紧急制动过程中，最高温度达到531K，最大应力达到414MPa，超出了蠕墨铸铁的强度极限。改用每轴安装3个制动盘的方案进行上述计算，分析结果见图5。

图4 制动盘有限元模型

图5 每轴3盘分析结果

图5（a）是在31s时，制动盘的温度达到最大时的温度云图，由图可知制动盘摩擦面上的温度比其他部位高，最高温度为452K。这是由于制动时闸片和盘面的摩擦接触是制动盘最主要的热输入，温度由盘面向周围传递，随着离盘面深度的增加，温度逐渐降低。

图5（b）是在对制动盘进行温度分析后，得出温度梯度最大的时刻出现在10.8s，将其温度结果作为体载荷施加到模型上，并在剖面施加对称载荷，盘面内表面施加全约束，在盘面与闸片接触部位施加均匀压力并施加制动减速度后，得出的应力云图。由图可知，制动盘摩擦部位出现应力最大区域，最大应力为295MPa，在蠕铁强度极限之内。

图5（c）是最高温度节点的温度时间历程曲线，由图可知，该节点的温度随时间的增加先变高，之后逐渐降低，这是由于起初由于盘面和闸片摩擦产生的热量大于盘面的传热及散热速度，致使温度升高，随着制动的进行，车速逐渐降低，摩擦产生的热量小于传热及散热量，使节点温度逐渐降低，最终在车辆停止后逐渐恢复大气温度。

4 结束语

以160km／h快速货车蠕墨铸铁制动盘为研究对象，在ANSYS中建立了循环对称三维模型，经过加载计算得到在160km／h初速度下施实紧急制动轴盘的温度场及应力场，计算分析结果表明在160km／h高速货车上应每轴安装3个制动盘，以降低制动盘的承载热量及应力，增加制动盘的安全性能。该计算结果对于快速货车制动盘的选材、设计分析具有一定的参考价值。

［1］吴萌岭.准高速客车制动盘温度场及应力场的计算与分析（上）［J］.铁道车辆，1995，33（9）：6-8.

［2］吴萌岭.准高速客车制动盘温度场及应力场的计算与分析（下）［J］.铁道车辆，1995，33（10）：33-38.

［3］王文静.SiCp／A356复合材料制动盘温度场应力场数值模拟及热疲劳寿命预测［D］.北京交通大学，2003.

［4］丁 群，谢基龙.基于三维模型的制动盘温度场和应力场计算［J］.铁道学报，2002，24（6）：34-38.

［5］李继山，林祜亭，李和平.高速列车合金锻钢制动盘温度场仿真分析［J］.铁道学报，2006，28（4）：45-48.

［6］林谢昭，高诚辉.盘式制动器非轴对称温度场的有限元模型［C］.疲劳与断裂工程设计论文集，西安，2002：404-407.

［7］钱坤才，张 棣.160km／h货物列车制动盘、闸片材料及制动性能试验研究［J］.机车车辆工艺，2008，（1）：2-7.

［8］张 奕.传热学［M］.南京：东南大学出版社，2004：130-134.