铁路斜交桥墩地震响应探讨

商耀兆

(铁道第三勘察设计院集团有限公司，天津 300142)

1 工程概况

新建旅顺经济开发区工业园区铁路专用线工程的线路等级为国铁Ⅱ级，荷载类型为中-活载，桥址处地震烈度为Ⅶ度，地震动峰值加速度0.1g，土壤冻结深度为0.93 m。

公路与铁路法向交叉角度为59°，土羊公路要求净空12 m×5.5 m+2 m+12 m×5.5 m，其中隔离带宽2.0 m。由于工点距离旅顺西站只有约260 m，线路纵断面抬高困难，所以桥梁的建筑高度受限，不能采用大跨梁方案。

土羊公路特大桥的6号墩位于公路隔离带内，地方要求不能侵占公路净宽，所以6号墩采用正顶帽、斜墩身结构，顶帽与墩身交叉角度达59°。平面布置如图1所示。

图1 墩台半基顶及半基底平面(单位:cm)

2 桥墩结构尺寸

6号墩采用圆端形实体桥墩，墩身高5.5 m，墩全高7.4 m，墩身纵桥向宽1.60 m，横桥向宽5.83 m，桥墩顶帽与墩身斜交，角度达59°，墩顶架设32 m预应力混凝土简支T梁。

土羊高速公路分两幅，每幅车道宽12 m，中间隔离带宽2 m，6号墩位于公路隔离带内，未侵占行车净空。

桥墩采用ANSYS建立实体模型，三维效果如图2所示。

图2 土羊公路特大桥6号墩三维效果

3 抗震分析计算方法

由不同的力学模型可分为全桥模型和单墩模型;由不同的抗震计算方法可分为反应谱法和时程分析法。

3.1 反应谱法

反应谱方法是目前结构抗震设计中广泛使用的方法。反应谱方法用于抗震设计包括2个基本步骤:第一步是根据强震记录统计用于设计的地震动反应谱;第二步是将结构振动方程进行振型分解，将物理位移用振型广义坐标表示，而广义坐标的最大值由第一步中的设计反应谱求得。

当n个质点体系地震振动时，其振动方程的矩阵表示形式为

式中 ［M］——质量矩阵;

［C］——阻尼矩阵;

［K］——刚度矩阵;

{I}——单位列矢量;

利用振型正交性，n个互不耦合或独立的运动方程为

式中 ξj——第j振型的阻尼比;

ηj——振型参与系数，ηj=

以广义坐标表示的微分方程式(2)的解为

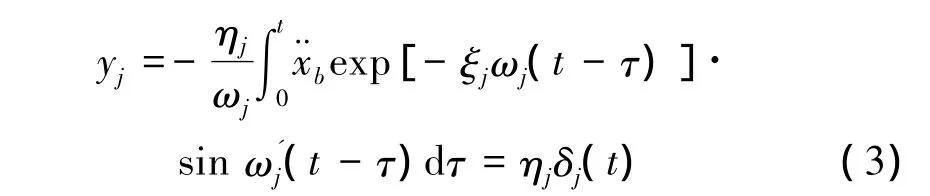
式中 δj——j振型等效单自由度体系(ω =ωj，ξ=ξj)位移地震反应。

多自由度弹性体系第j振型的第i个质点所受的最大地震作用为

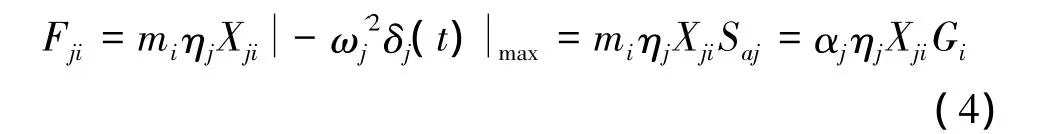
式中 Fji——相应于j振型，质点i的最大水平地震作用;

αj——相应于j振型结构自振周期的水平地震影响系数值;

Saj——相应于j振型最大绝对加速度;

Xji——第j振型的质点i处的幅值;

Gi——i质点的重力荷载代表值。

3.2 时程分析法

动态时程分析方法是随着强震记录的增多和计算机技术的广泛应用而发展起来的，是公认的精细分析方法。目前，大多数国家除对常用的中小跨度桥梁仍采用反应谱方法计算外，对重要、复杂、大跨度的桥梁抗震计算建议采用动态时程分析法。

动态时程分析方法能够比较准确地确定结构在地震过程中结构的内力和位移随时间的反应，并发现结构在地震时可能存在的薄弱环节和可能发生的震害。

在地震反应中，地面振动加速度是复杂的随机函数，对于这种有较复杂激振力，可采用逐步积分法求动力响应问题。其基本思想是把时间离散化，如把时间区间T分为T/n=Δt的n个间隔。由初始状态t=0开始，逐步求出每个时间间隔末 Δt，2Δt，…，T上的状态向量(常由位移、速度和加速度等组成)。最后求出的状态向量就是结构系统的动力响应解。在这种方法中，后次的求解是在前次解已知的条件下进行的。开始是假定t=0时的解(包括位移和速度)为已知，求出Δt时的解，接着再以Δt时刻的已知解计算2Δt时刻的解，如此继续下去。

3.3 简化公式法

《铁路工程抗震设计规范》(GB50111—2006)(2009年版)中规定，简支梁桥墩的水平地震作用可按规范中附录E的简化公式计算。规范中公式，在此不再赘述。

4 不同计算方法结果及分析

4.1 计算模型

用有限元软件MIDAS建立全桥模型，分别采用反应谱法和时程分析法进行计算，其中时程分析法选用了EI Centro 270度波(简称 EI1)、EI Centro 180度波(简称 EI2)、Taft 69度波(简称 Taft1)、Taft 339度波(简称Taft2)等四条地震波，MIDAS模型及地震波如图所3～图7所示。

图3 抗震分析全桥模型

图4 EI Centro 270°波

图5 EI Centro 180°波

图6 Taft 69°波

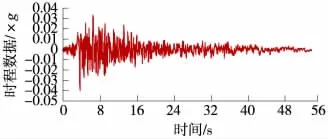
图7 Taft 339°波

4.2 振型分析及控制工况选取

对桥跨结构进行模态分析，前四阶振型如图8～图11所示。

图8 第一振型

图9 第二振型

图10 第三振型

由以上分析可见，对6号墩而言，桥跨结构的前三阶振型均较多地偏向墩身的纵向，第四振型较多的偏向墩身的横向。所以控制工况除了规范规定的纵桥向和横桥向以外，本文还选取了6号墩的墩身纵向和墩身横向作为比较工况。

图11 第四振型

4.3 计算结果

反应谱法及时程分析法，分别计算了纵桥向、横桥向、6号墩墩身纵向、墩身横向4种工况。

计算结果如表1、表2所示。

表1 反应谱法计算各工况下内力结果 kN·m

表2 时程分析法计算各工况下内力结果kN·m

各工况下墩底钢筋拉应力如图12所示。

图12 各工况下墩底钢筋拉应力

由图12可见，反应谱法与时程分析法的计算结果吻合较好，尤其是沿墩身纵向作用和沿墩身横向作用的结果更加相近。

用《铁路工程抗震设计规范》中简化公式计算，沿墩身纵向作用的纵向弯矩为4 890.2 kN·m，沿墩身横向作用的横向弯矩为4 939.1 kN·m。所产生的钢筋拉应力分别为190.2 MPa和76.4 MPa。

4.4 结果分析及结论

由以上计算结果及对比，可得出以下结论。

(1)对比顺桥向作用、横桥向作用、墩身纵向作用和墩身横向作用等4种工况，可知墩身纵向作用时的墩底钢筋拉应力最大。墩身纵向也是桥墩的第一阶振型方向。《铁路工程抗震设计规范》中7.1.4条规定“桥梁抗震检算时，应分别计算顺桥向和横桥向的水平地震作用。”所以此规定不完全适用于斜交桥墩，笔者建议还应计算桥墩第一阶振型方向的地震作用。

(2)对比时程分析法、反应谱法和规范简化公式法等三种计算方法，可知时程分析法与反应谱法的计算结果非常相近，尤其是沿墩身纵向作用和沿墩身横向作用的结果吻合较好;而规范简化公式法不能考虑桥墩两侧梁跨对桥墩地震响应位移约束的影响，使得桥墩纵向的作用效应偏大，桥墩横向的作用效应偏小。反应谱法计算简便，所以建议对于此类工点宜建立全桥模型并采用反应谱法计算。

(3)另外应注意，建立模型时应考虑基础刚度的影响，可建立节点局部坐标系，按实际方向输入基础弹簧刚度。

5 结语

正顶帽、斜墩身的结构形式能较好地解决跨越立交道路时的净空受限问题，进行抗震分析时，宜建立全桥模型，采用反应谱法进行计算，并且应计算桥墩第一阶振型方向的地震响应。

［1］中华人民共和国铁道部.TB10002.1—2005 铁路桥涵设计基本规范［S］.北京:中国铁道出版社，2005.

［2］中华人民共和国铁道部.TB10002.3—2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.北京:中国铁道出版社，2005.

［3］中华人民共和国铁道部.GB50111—2006 铁路工程抗震设计规范(2009年版)［S］.北京:中国计划出版社，2009.

［4］中华人民共和国铁道部.TB10002.5—2005 铁路桥涵地基和基础设计规范［S］.北京:中国铁道出版社，2005.

［5］范立础，胡世德，叶爱君.大跨度桥梁抗震设计［M］.北京:人民交通出版社，2001.

［6］裘伯永，盛兴旺，乔建东，等.桥梁工程［M］.北京:中国铁道出版社，2005.

［7］胡聿贤.地震工程学［M］.北京:地震出版社，1998.

［8］倪燕平.《铁路工程抗震设计规范》的修改及对铁路桥桥墩的影响［J］.铁道标准设计，2005(11).

［9］廖振鹏.工程波动理论导引［M］.2版.北京:科学出版社，1996.

［10］范立础.桥梁抗震［M］.上海:同济大学出版社，1997.