基于线性预测的自适应语音压缩感知
赵 翠,周 遥,毛鑫萍,马永阳
(浙江工业大学信息工程学院,浙江杭州310023)
0 引言
压缩感知(Compressed Sensing,CS),是近年来兴起的信号压缩采样技术,利用信号的稀疏性或可压缩性,采用非自适应采样技术将原始信号的信息投影在少量观测数据中,在采样过程中同时实现压缩[1,2]。由于CS理论的特性,其在语音信号处理领域的应用有着巨大前景。CS理论应用的一个重要前提和基础是稀疏性,只有选择合适的基才能保证信号的稀疏度,从而保证信号的重构性能。因此构造语音信号的稀疏变换基是CS应用于语音处理的重要前提。中外一些文献从不同角度研究了适合语音的稀疏变换基,如基于PCA构造冗余字典,混合字典等[3-5],为语音信号压缩感知的应用提供了思路和方法。本文主要利用线性预测(Linear Prediction,LP)技术[6],研究适合语音压缩感知的稀疏变换基。与文献5中直接构造每帧语音的稀疏变换基不同,本文基于帧间的相关性,提出了自适应LP基,大大降低了传输量,同时保证了重构性能。
1 压缩感知理论
压缩感知理论认为,如果信号在某一变换域上是稀疏的,那么就可以用此信号在某投影域上的观测集合来近似无损地重构原始信号[7]。给定长度为N的实值信号x∈RN,如果该信号在某一个正交基或紧框架 Ψ:Ψ= [ψ1,ψ2,…,ψN]上的变换系数是稀疏的,即x可以表示成:

式中,s是信号x在Ψ上的变换系数向量,而且只有K(K≪N)个非零元素,因此x称为在Ψ域上K-稀疏。如果用一个与稀疏变换基Ψ不相关的观测矩阵Φ∈RM×N(M≪N):Φ=[φ1,φ2,…,φN]将原始信号投影到低维空间,得到观测集合y∈RM:

那么就可以利用优化求解方法从观测集合中精确或高概率地重构原始信号x。对于给定的观测集合y,观测矩阵Φ和稀疏变换基Ψ,CS的重构算法就是利用0-范数解决优化问题:

然而实际上,式3的求解是一个NP难题,根据文献1指出,在Φ和Ψ不相关的情况下,将1-范数代替0-范数会产生同等解。因此可以将式3的优化问题转化为凸优化问题进行求解:

目前,追踪贪婪算法、凸松弛法和组合算法是3类主要的CS重构算法。
2 自适应语音压缩感知
LP是语音信号处理的一个核心技术,广泛地应用于语音压缩、识别等各方面。由于语音样点之间的相关性,LP的基本思想就是过去的p个语音样点的线性组合来预测现在或未来的样点值x(n),预测的残差用e(n)表示:
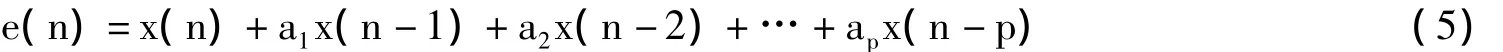
式中,{ai}是LP系数集,LP分析是求解LP系数集使得残差e(n)在某个预定的准则下最小。设一段语音信号x,语音帧长为N,则根据式5,第k帧语音信号xk和其对应残差信号rk可以用下式表示:

式中,xk[x((k-1) N+1) x((k-1) N+2)…x( kN)]T表示一段语音信号 x的第 k帧,ek≜[e((k-1) N+1) e((k-1) N+2)…e( kN)]T,Ak由xk的 LP系数集 ak={aki}构成:


式中,Ψk为Ak的逆矩阵,称为LP基。因为语音信号经过LP后其残差信号近似于稀疏信号,所以第k帧信号xk在Ψk上被认为是稀疏的。然而根据语音的短时平稳特点,有些连续的语音帧之间存在很大的相关性,当前语音帧的LP基可以用前一帧的LP基代替,而不影响当前语音帧的稀疏性。此时当前语音帧无需LP分析,也无需传输自身的LP系数ak。然而又由于语音的非平稳性,有些语音段的相邻帧相关性很小,此时当前语音帧则需要LP分析,构造使得当前帧稀疏的LP基。通过此方法构造的稀疏变换基,称为自适应LP基。根据前面的分析,构造自适应语音压缩感知框架,如图1所示。
式6可以改写为:

图1 自适应语音压缩感知框架
图1中Rk表示相邻两帧语音xk和xk-1之间的相关性:
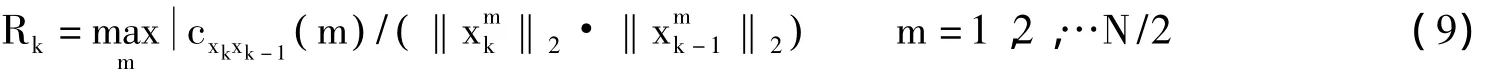
3 实验结果及分析
实验主要研究语音在自适应LP基下的CS性能,并与非自适应LP基及DCT基方案下的CS性能进行比较,根据平均帧信噪比来测试重构语音性能:
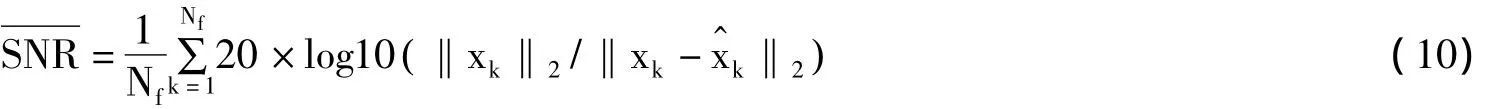
式中,Nf表示帧数表示第k帧重构语音。实验中采取一段采样率为16kHz的语音信号,帧长N=320,LP的阶数p=10,LP系数集ak采用网格结构的burg算法求解,相关性的阈值TR=0.7。观测矩阵Φ采用一致球形矩阵,M=80,重构算法采用正交匹配追踪算法,该重构算法的循环终止条件设置为:重构稀疏向量的非零个数lK=40,或误差满足error≤10e-7。
3帧和30帧语音信号的CS重构语音的波形比较,如图2、3所示。图2、3(a)表示原始语音信号,图2、3(b)表示采用自适应LP基的重构语音,图2、3(c)表示采用非自适应LP基的重构语音,图2、3(d)表示采用DCT基的重构语音。各方案所对应的重构性能和所需传输LP系数组数如表1所示,表1中的(a)(b)(c)(d)如前所述。
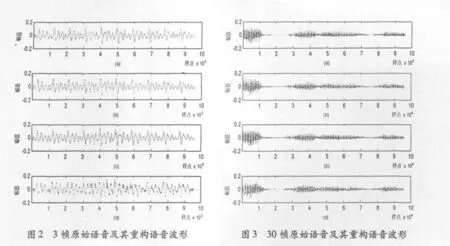

表1 自适应LP基与非自适应LP基及DCT基的比较
从表1中可以看出,连续的3帧语音信号很相似,即相关性很大,后两帧信号直接使用第一帧的LP基的自适应重构性能与使用自身生成的LP基的非自适应重构性能类似,而且减少了传输量。30帧的语音信号采用自适应LP基的重构性能与采用非自适应LP基大致相同,而且减少了12组LP系数组的传输,在保持重构性能不变的同时,降低了传输量。虽然DCT基是固定的,但其重构语音与采用自适应LP基的方法相比,性能较差。
4 结束语
本文从自适应的角度研究了压缩感知在语音信号中的应用。根据语音信号经过线性预测后的残差信号近似稀疏的特点,构造LP基作为压缩感知的稀疏变换基。同时利用语音信号连续帧之间的相关性,构造了自适应LP基。本文提出的基于帧结构的自适应LP基与非自适应方法相比,减少了传输量,同时保持了非自适应方法的重构性能,且远优于采用DCT基的重构性能。这在语音信号的编码速率和合成语音质量方面有很大的作用。
[1] Donoho D L.Compressed sensing[J].IEEE Trans on Inf Theory,2006,52(4):1 289-1 306.
[2] Candes E,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly in complete frequency information[J].IEEE Trans on Inf Theory,2006,52(2):489-509.
[3] 季云云,杨震.基于主分量分析的语音信号压缩感知[J].信号处理,2011,27(7):1 057-1 062.
[4] Giacobello D,Christensen MG,MurthiM N,et al.Retrieving sparse patterns using a compressed sensing framework:Applications to speech coding based on sparse linear prediction[J].IEEE Signal Processing Letters,2009,17(1):103-106.
[5] Wang Y,Xu Z X,LiG,et al.Compressed sensing framework for speech signal synthesis using a hybrid dictionary[C].Shanghai:Image and Signal Processing,2011:2 400-2 403.
[6] 王洪,唐凯.低速率语音编码[M].北京:国防工业出版社,2006:20-25.
[7] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1 070-1 081.

