基于约束规划的编组站阶段作业计划优化研究
张雪松,马 亮
(1.铁道部 信息技术中心,北京 100860;2.西南交通大学 信息科学与技术学院, 成都 610031)
编组站是铁路枢纽的核心,是车流大量集散的基地,其作业组织效率直接影响着铁路枢纽乃至整个路网的效率。在目前中国铁路的组织型运输模式中,编组站的作业组织包括作业组织计划、行动计划和具体行动计划3个层次。其中,作业组织计划包括日/班计划,它们对应于铁路局的日/班计划,用来对当日/当班的生产经营任务进行总体安排和宏观组织;行动计划指阶段作业计划,用来组织一个3 h~4 h阶段的具体作业安排,要具体考虑作业能力的限制和运输资源的合理运用;具体行动计划即调车计划,是对实际车辆位移活动的具体安排。3个计划中,阶段作业计划起着承上启下的作用,既要考虑保证日/班计划的实现,又要考虑各种实际资源限制,是整个编组站作业指挥的核心,也是编组站运输组织优化的关键。
1 编组站阶段作业计划介绍
从优化的角度讲,编组站阶段作业计划的内容包括:到发线使用计划、本务机走行计划、驼峰/调机使用计划、配流方案/解编(含取送)顺序4个部分。优化的内容包括运力资源的分配和作业顺序的确定。其中运力资源包括到/发线、本务机、驼峰、调机、分类线等,作业包括到达技术作业、推峰-解体、编组、出发技术作业、出发,以及取送、装卸、机车整备等。最核心的业务是解体—编组作业,最稀缺的资源是驼峰和分类线,因此,配流方案/解编顺序的确定是整个计划的核心。在本质上,两者是同一问题的两个方面。确定解编顺序的目的是为了优化车流接续方案,确定了解编顺序,配流方案就迎刃而解,两者是密不可分的,需要同时考虑。解编顺序一旦确定,就可以利用计算机精确地推算阶段内任意时刻的现场状态,并在此基础上安排、优化到发线使用、本务机走行和驼峰/调机使用计划。
在设计配流方案/解编顺序时,不可避免地涉及到出发列车计划的确定。按照规定,出发计划应由铁路局计划调度员下达。但是在实际作业中,由于车站调度人员对站内车流和技术设备情况掌握比较细致、准确,也经常需要参与出发计划的确定,因此,在考虑配流方案时,必须同步考虑出发列车方案,否则,所形成的方案就无法真正运用到生产实践。
综上所述,编组站阶段作业计划优化的核心是包含出发列车计划的配流方案/解编顺序的确定。计算机对上述问题的求解,可划分为3种思路。思路1:经验法。即根据现场作业人员的经验,模拟人的思维、行为模式,设计特殊算法求解。这类方法基本上是基于先到先解的顺序进行局部优化、调整,虽然在个案上不乏实用的样例,但很难形成通用系统。思路2:基于经典运筹学理论的研究。这方面的研究论述甚多[1~4],例如将配流转换为运输问题,运用表上作业法进行求解。对阶段计划DSS中的优化模型进行了全面构造和综合集成,并针对这一问题形成了实用系统,在丰台西等站进行了大量实践。但总的说来,由于中国铁路运输非常复杂,配流的理论研究还未能取得突破性成果,还没有形成具有通用性的应用。 思路3:非经典优化方法[5~6]。所谓非经典优化方法,是相对经典运筹学理论而言的,门类较多。如约束规划、产生式系统、启发式算法等都属于这一范畴。利用遗传算法求解进行解编顺序的方法,即属于非经典方法。编组站配流问题属于组合优化问题。它涉及因素众多,各因素之间的关联千丝万缕,模型异常复杂,不具有良性结构,经典算法难以发挥其长处。相比之下,非经典方法通常能更贴近生产实践,而且不需要高深复杂的数学理论知识,更能为现场人员所接受,并且能够让实践经验丰富的业务人员参与到项目研发过程中来,更易于发挥经验和主观能力的作用,更加适合编组站阶段计划的优化问题。
本文基于约束规划理论,依托IBM ILOG工具,结合多年的编组站应用和优化研究实践,提出了一套求解编组站阶段作业计划生成与优化的方法体系,并就其核心算法—配流方案/解编顺序问题建立了数学模型,给出计算机实现方法。
2 基于约束规划求解的基本思路
约束规划[7](Constraint Programming)是解决约束满足问题(CSP,Constraint Satisfaction Problem)的方法。一个约束满足问题包括有限变量集、每个变量的有限论域和有限约束集。每条约束限制了变量集赋值的组合。约束满足问题的解是为每个变量赋一个对应论域上的值,使之满足所有的约束。求解约束满足问题的目标是找到一个可行解或是全部可行解。约束规划广泛地借鉴了人工智能、计算机科学和运筹学的技术,从某种意义上讲,与数学规划(Mathematical Programming)类似,用户可以定义决策变量、声明优化目标,并指定关于决策变量可行解的一组约束。
借助于IBM ILOG工具,研究人员可以将精力聚焦到描述业务目标和约束上来,而不去关心具体的实现细节。当确认所建模型能够得到满意解后,再集中精力研究模型优化,解决性能问题。按照这种思路,在早期建模阶段,可以邀请业务人员参与,分享其业务经验,使模型在设计之初就能从实际出发,贴近现场的作业习惯和思维方式。即使在后期调优阶段,业务人员仍然能发挥较大作用,根据经验增加约束,有效地缩减解空间规模。
求解约束规划的关键是性能问题。当决策变量达到一定规模时,其性能会发生突变。因此,在建立约束规划模型时,首先要分解问题域,在不破坏业务完整性和连续性的前提下,把复杂问题分解成一系列简单问题。同时,要根据约束规划的特点设计应用,将数据预处理,结果的细化、校验、修正剥离出来,约束规划只负责最核心的配流和解编顺序的确定。这一思路使应用程序设计和约束规划算法设计全面结合起来,两者相得益彰,充分发挥各自的优势,最终构建成统一、完整的应用系统。
按照上述思路,设计的求解编组站阶段作业计划生成与优化问题的基本步骤如下:
(1)从编组站管理信息系统提取数据。包括编组站结存车辆、到达场到达列车、预计到达列车(预确报)、出发场待发列车、铁路局下达的班计划、当前阶段作业计划、已编制的调车计划等。
(2)调用编组站管理信息系统的推流服务,推算出待编阶段起始时刻的车流。
(3)对步骤(2)推算的车流数据进行预处理,挑选出不参加编组的车辆(如扣修车、本站待卸车等),并将其余车辆(即参加编组车辆)按特征分组。经本步处理后,车流分类一律用方向号表示,不再使用重车按方向、空车按车种、非运用车按标记的分类表示方式。
(4)计算每列列车解体需要的时间。解体时间包括推峰时间和分解时间两部分。分解时间按解体钩数和送禁溜次数计算。
(5)对班计划(或编组计划)的出发计划进行整理,计算并表示出每列车的编组内容、最晚开编时间(在此前所有相关到达列车的解体工作都要完成)、够轴条件(本步骤按车数掌握)等。
(6)调用约束规划算法,求解以下决策变量值。决策的结果通常不只是一个可用解,而是一组可用解。决策内容包括:
a.决定每列到达列车的推峰时间、开始解体时间和解完时间;
b.决定哪些出发列车被选用;
c.决定所选用出发列车的编组内容;
d.决定每个出发计划的牵出时间。
(7)对规划结果进行校验、完善、修正,包括确定每列出发列车的具体车流来源,精确计算轴重和轴长,检验编组隔离限制,以及为每项任务分配具体驼峰、调机等资源。在步骤(6)中,出于效率考虑,驼峰等资源均是作为资源池考虑,仅约束了其能力(并行作业数量),而没有分配到具体资源,因此,需要在事后再次分配具体资源。
(8)按照步骤7得出的结果,安排到发线使用等其它计划。
(9)将结果提交给编组站管理信息系统,由系统展示给站调,通过交互确认计划。
上述步骤是我们在多次实践中提炼、总结出来的。其中决策的关键点是步骤(6)“调用约束规划算法求解”。下面重点剖析该步骤的算法模型。
3 算法模型
基于约束规划求解配流方案/解编顺序问题的基本元素是车辆。为缩减算法规模,降低决策变量数量,采用了车组表示车流的方式,在模型中不考虑具体车辆。这种方式在判断列车满轴时只能通过车数判断,可能造成一定失真,但决策变量得到了大幅度削减。而由于失真所产生的问题,可以在后续处理中通过计划微调进行解决,不会影响决策结果。
采用了列车—车组表示车流的简化模型可描述如下:
阶段时间[ts,te]内,m个编组方向组成集合为D={d1,d2,…,dm}。为统一表示,所有车辆,包括空车、非运用、作业车等均用方向表示。
mA个到达列车组成集合为A={ai|ai=
mF个出发车组成集合为F={fj|fj=
决策包括两项内容:
(1)到达列车解体开始时间集合S={s1,s2,…,sm},其中si为到达列车ai的开始解体时间;
(2)出发列车计划集合为DF={dfj|dfj=
车组建模的关键,是按车流方向表示到发接续关系,模型中仅完成到达解体时间、出发编组时间和出发车流组成的决策,而不进行具体配流方案的制定,从而提高算法效率。算法的核心是车流表示。在ILOG环境下,通过车流累积函数(Cumulative Function)的概念来表示某一方向的车流随着作业的动态变化。
定义1:车流累积函数是阶跃函数,具体表现为:以时间为横轴,车流数为纵轴,车流随着各作业的实施而进行累加或者累减。记(+/-)Θ(n,t),表示t时刻累加/累减了n个车流;(+/-)Θ(0,n,t),表示t时刻累加/累减[0,n]个车流,其中,n,t∈Z*。
定义2 :车流累积函数的高度(+/-)heightAt(Θ,t)表示时刻t累积函数Θ的变化值,为正数。

图1 车流累积函数
图1 为车流累积函数,分别累加了n1和[0,n2]个车流,累减了n3个车流。
通过上述分析得到模型的决策变量和决策表达式,包括:
(1)到达车开始解体时间:S={s1,s2, …,sm};
(2)出发车决策内容:DF={dfj|dfj=
(3)整个阶段时间各方向车流累积函数:
(∨i∨j∨k)Ni,j,k=Θ(nik,si)-Θ(0,fullj,tmj)g λjk
(4)出发车fj使用到达车ai方向dk的车数:(∨i∨j∨k)HZi,j,k=-heightAt(Ni,j,k,tmj)gλjk出发车满轴约束条件如下:

模型的目标为出发车最多:

4 模型求解
本研究通过约束传播机制和搜索策略[10~11]对模型进行求解,其中约束传播机制分为:初始化约束传播和搜索过程约束传播,主要目的是对可行解域进行缩减。初始化约束传播是在初始可行解集的基础上删除那些不可能成为解的那部分域;而搜索过程约束传播与搜索策略结合在剩余搜索空间的基础上删除那些不满足约束的解集,并通过搜索树对解进行搜索。
4.1 利用初始化约束传播得到初始解
本研究采用系统搜索算法获得初始解,先确定源车流的解体顺序和出发车的编组顺序,然后对目标函数进行枚举赋值以找到可行解,主要流程如图2。

图2 初始解生成流程图
4.2 用搜索技术结合过程约束转播改进初始解
得到初始解后,将它作为当前解,利用禁忌搜索算法的邻域函数随机改变当前解的调整模式的某一个分量,产生相对于当前解的移动。这里,调整模式是指所有调整变量的一组取值。在每一步移动之后,利用约束传播算法求解批量变量,并计算目标函数值。选择邻域中非禁忌或解禁后目标函数值最大的解编顺序作为新的当前解,继续产生移动得到新的解,从而不断地对解进行改进。禁忌搜索流程如图3。
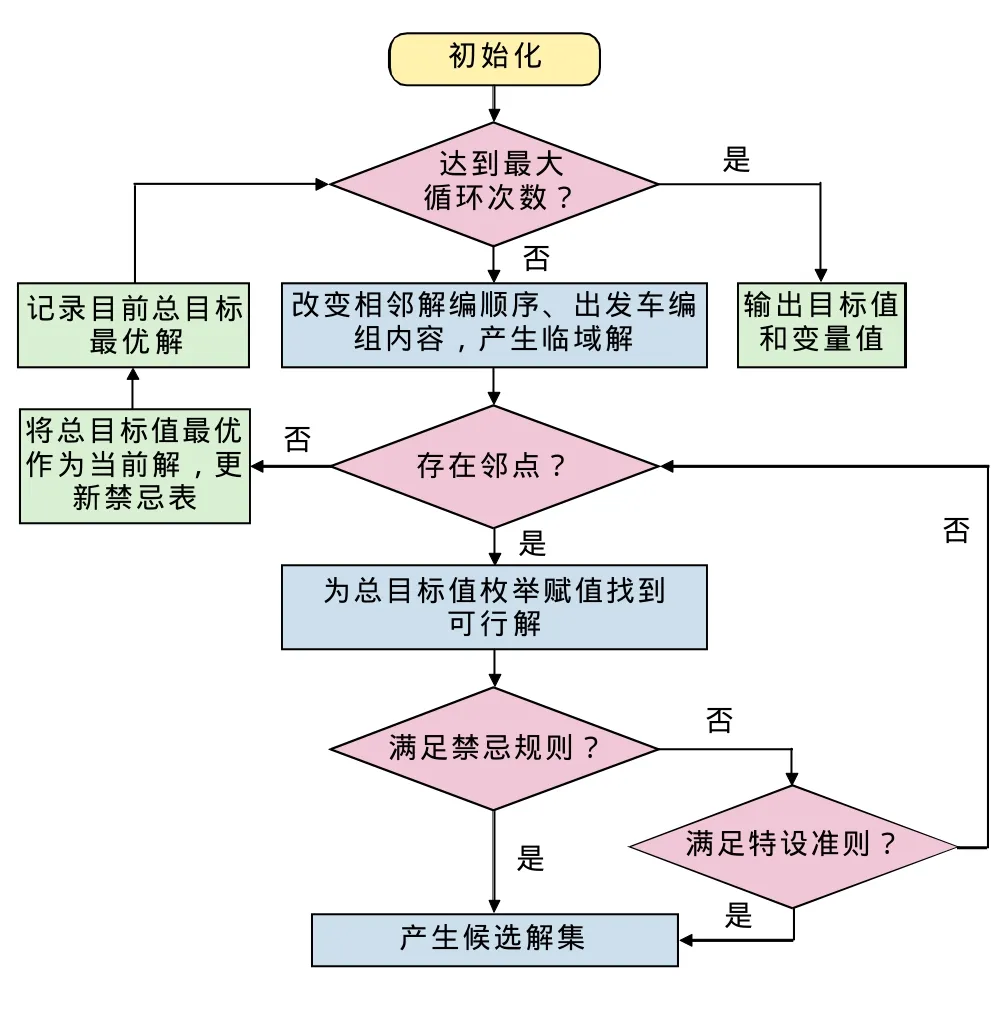
图3 搜索技术搜索最优解
5 结束语
本文在对编组站阶段作业计划优化问题系统分析的基础上,提出了求解的基本方法,并对方法的核心部分建立了基于约束规划的模型和求解方法。方法经大量现场数据仿真试验,已基本接近人工编制计划的水平。后续工作中,我们准备从业务和技术两方面努力。在业务方面,通过比对模型结果,发现模型的不足,不断修改、增加约束条件,使结果更加优化,逐渐赶上并超过人工编制的水平,增强算法的适用性。在技术方面,深入探索,不断提高算法的性能,保证能够满足现场作业的时间要求。
本文介绍的优化方法的目标,锁定在编组站综合自动化系统的“智能化”领域,期望通过计算机替代人的脑力劳动,实现编组站运输组织的宏观优化,推动编组站自动化水平的不断提高。更进一步,依托本算法良好的说明特性和联合求解的优势,可以将它运用于铁路局计划调度应用,实现局站一体化的目标。
[1]王慈光.用表上作业法求解编组站配流问题的研究[J]. 铁道学报,2002,24(4):1-5.
[2]何世伟,宋 瑞,朱松年. 铁路编组站阶段计划编制的模型及其算法研究[J].系统工程理论与实践,1997,2(2):88-94.
[3]薛 锋,王慈光,罗 建. 双向编组站静态配流的优化[J].西南交通大学学报, 2008,43(2):159-164.
[4]崔炳谋. 铁路编组站综合自动化若干问题的研究[D]. 北京:铁道科学研究院,2005:3-6.
[5]王世东,郑 力,张智海,等. 编组站阶段计划自动编制的数学模型及算法[J].中国铁道科学,2008,29(2):120-125.
[6]姜英新,孙吉贵. 约束满足问题求解及ILOG SOLVER系统简介[J]. 吉林大学学报(理学版),2002,(1):53-60.
[7]竺 东,杨建军.基于约束规划的调整时间与顺序有关的Job Shop调度研究[J]. 先进制造工艺技术,2007,24(2):53-63.

