一种圆环面刀具五坐标端铣加工局部干涉检测算法
谭建新
(娄底职业技术学院机电工程系,湖南娄底 417000)
0 引言
复杂曲面在航空航天、汽车、轮船及模具行业中得到了广泛应用,这些曲面通常需要依靠五坐标数控铣削加工来完成,其中刀具与工件曲面的干涉检测一直是该领域的重点和难点之一,国内外很多学者对此进行了研究。通常刀具与工件曲面的干涉可分为局部过切和全局干涉两类。其中,局部过切代表刀具刀头部分和工件曲面在局部范围内的干涉,而全局干涉是指刀柄与工件及夹具等的干涉。目前,已有的干涉检测方法主要有多面体法[1]、直接距离计算法[2-4]、刀具与曲面离散法[5-6]、凸包法[7-9]及其它专用算法[10-11]等。由于刀具类型及曲面加工形式的不同,几乎所有的算法都有一定的应用局限性。针对圆环面刀具和端铣刀,陈丽萍等[4]提出了一种局部过切检测算法,该方法利用赋范空间投影算法求圆环面刀具环心圆到工件曲面的最小距离来进行干涉检测,算法简单且计算效率高。龚堰珏等[12]指出这种赋范投影算法对于复杂曲线曲面可能存在发散的情况,由此提出了一种改进的几何迭代算法。基于此,本文借鉴了这种思想,提出了一种稳定易收敛的适用于圆环面刀具五坐标端铣加工的局部干涉检测算法,并通过一个例子对算法的正确性和有效性进行了验证。
1 圆环面刀具五坐标端铣加工特性
在复杂曲面端铣加工领域中,刀位算法一直是研究的热点和难点。刀位算法被用来确定刀具相对于工件曲面的位置,目的是使刀具与工件曲面在不发生过切的前提下从工件毛坯中去除尽可能多的材料。目前应用最广泛的刀位算法是刀轴倾斜法,它已经作为通用算法被集成到商业软件如UG、Mastercam中。对于球头刀五坐标端铣加工而言,只需要根据刀触点处法矢量和刀具半径即可求得刀心点坐标,刀轴矢量也可由法矢量和进给方向来简单确定,而圆环面刀具则要复杂的多。
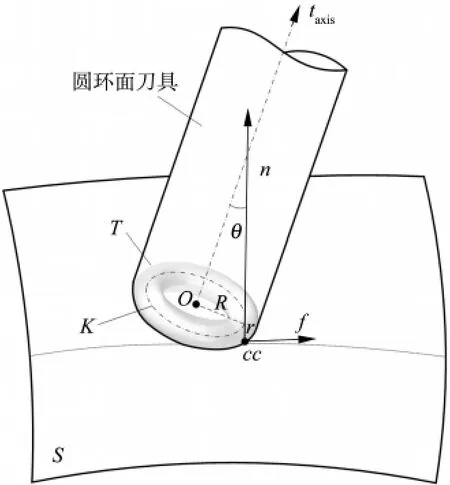
图1 圆环面刀具端铣加工
图1为用圆环面刀具进行曲面端铣加工的示意图,其中S代表工件曲面,T代表圆环面刀具的工作切削面即圆环面,K代表T的环心圆,O为T的几何中心,R和r分别代表T的环心圆半径和圆角小半径。cc代表一条刀路轨迹上圆环面刀具和工件曲面S之间的切触点,n代表工件曲面S在cc点处的法矢量,f代表刀具进给方向,taxis代表圆环面刀具的刀轴矢量。根据圆环面的空间几何性质,容易知道法矢量n和环心圆K一定是相交的。基于刀轴倾斜法基本原理,刀轴矢量taxis一定位于由切触点处法矢量n和刀具进给方向f确定的平面内且与n的夹角为θ,则可以确定圆环面刀具的定位,其中θ被称为Sturz角。
刀轴倾斜法倾向于使用固定的角度θ来完成整个曲面加工所需刀位处的刀具定位,由于曲面的复杂性,在一些刀位处,刀具和曲面的局部干涉是不可避免的,因此需要针对每个刀位处进行局部干涉检测,然后通过调整角度θ来得到没有局部干涉的优化刀位。圆环面刀具端铣加工局部干涉检测问题实际上是刀具圆环面和工件曲面之间的面面关系。为了简化问题,可将圆环面刀具与理想曲面的几何相对关系简化为刀具环心圆K到工件曲面S的最小距离问题。用lmin代表该最小距离,当lmin小于圆角小半径r时,圆环面刀具和工件曲面S之间发生了局部干涉,此时最大干涉量dmax可以通过dmax=r-lmin计算出来。根据dmax可以进行刀位调整从而得到无局部干涉的刀位,因此圆环面刀具曲面端铣加工的局部干涉检测问题就转化成计算K到S的最小距离问题。
2 局部干涉检测算法原理
2.1 算法原理
在图2中,N0、N1和 N 为曲面 S上的点,M0、M1和M为刀具环心圆K上的点,t0、t1和t分别代表环心圆K在M0、M1和M 处的参数,t0、t1和 t分别代表刀具环心圆K在点M0、M1和M处的切矢量,Δt代表刀具环心圆K上相邻迭代点间参数t的增量。圆环面刀具局部干涉检测算法的具体实现步骤如下:
(1)将刀具环心圆K按照参数t均匀离散,分别求该10个离散点到曲面S的最小距离,将使得距离最小时曲线曲面上的点位信息作为初始迭代信息:点 M0、N0、切向量 t0和参数 t;
(2)把问题考虑为求曲面上点N0到刀具环心圆K的最小距离问题,此时将M0看作刀具环心圆K上的初始迭代点,根据点到曲线最小距离算法容易得到迭代步长Δt,根据t1=t0+Δt得到刀具环心圆K上的新迭代点M1和新的切向量t1,调用求点到曲面最小距离算法,可以得到点M1在曲面上的投影点N1;
(3)重复以上过程,经过若干次迭代,当|Δt|<10-6时停止,程序结束。
此时刀具环心圆K上的点收敛于点M,MN垂直于曲线在点M处的切向量t,同时点N为点M在曲面S上的投影,因此MN的长度即为算法所求的最短距离。
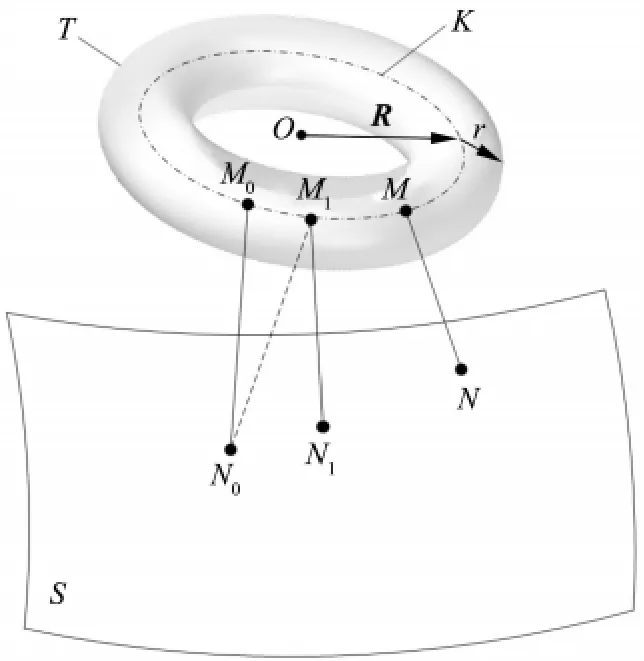
图2 圆环面刀具局部干涉检测算法
2.2 刀位修正处理
利用上述所提出的算法对整个曲面所有刀位进行局部干涉检测,对于存在局部干涉的刀位,必须进行刀位修正。刀位修正的基本思想是调整圆环面刀具的刀轴矢量即调整刀具后跟角θ,从而避免刀具和加工表面的局部干涉。刀位修正过程可以通过迭代判断来实现。
3 计算点到曲面的最小距离
由上可知,圆环面刀具局部干涉检测算法是通过轮流求点到曲线最小距离和点到曲面最小距离来完成的,而这些都是可以通过赋范空间投影几何迭代算法来实现,这两种几何迭代算法同时具有效率高且稳定的特点。点到曲线的最小距离算法相对简单,下面介绍一下点到曲面的最小距离算法。

图3 空间点到曲面最小距离迭代算法
在图3中,空间一点P,Su和Sv分别是曲面S在初始迭代点Q0的两个关于参数u和v的偏导数,假定曲面是正则的,则在任意点处两个偏导数的叉积不等于零。则迭代步长Δu和Δv可以通过下面的方程组计算出来。
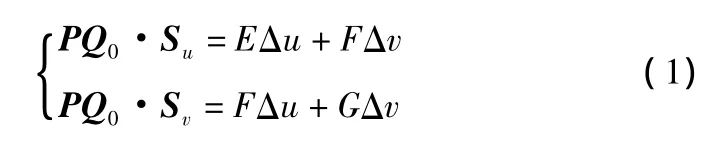
其中E、F和G为曲面S在点Q0处的第一基本量。计算出Δu和Δv以后,将得到的曲面上的新点作为新的初始迭代点,重复以上过程,直到|Δu|<10-6及|Δv|<10-6同时满足时停止,此时即可求得精度要求范围内P点在曲面S上的投影点Q。
4 算法实例
选用双参数曲面S(u,v)来验证本文所提出的局部干涉检测与修正方法,它的曲面方程由下式决定。
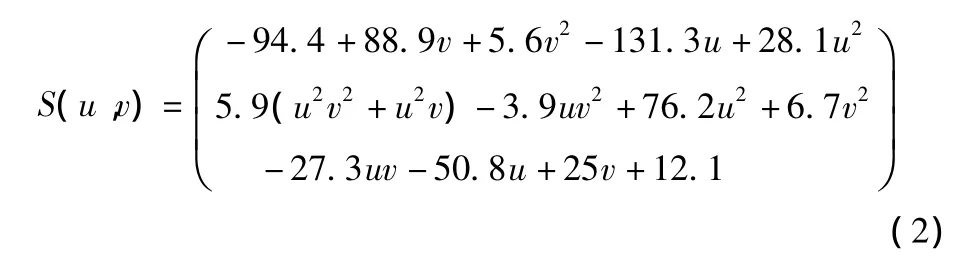
圆环面刀具参数为:R=10mm和r=3mm。使刀具进给方向f与曲面v参数一致。已知在由参数(u,v)=(0.5,0.5)决定的刀位处,有刀具倾斜角θ=5.118,利用本文提出的局部干涉检测算法对该刀位进行检测,可以得到使得圆环面刀具环心圆K到参数曲面S(u,v)达到最小距离时的对应点,有:M(-53.22,-64.73,17.09)和 N(-52.71,-65.47,14.34),如图4所示,最小距离lmin可以计算出来,为lmin=2.8996mm。由于lmin<r,可以判定圆环面刀具和参数曲面S(u,v)在该刀位处发生了干涉,且干涉量dmax=r-lmin=0.1004mm。此时需要调整刀轴矢量即调整θ角的大小对该刀位处进行修正处理。通过迭代判断,得到当θ=5.847时,lmin=3.000mm,此时局部干涉可以得到有效的避免。
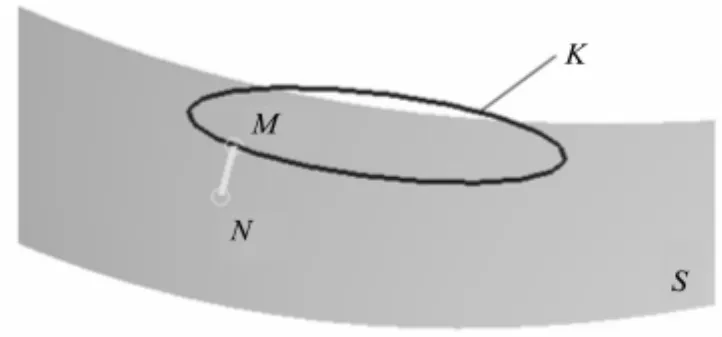
图4 局部干涉算法的验证
表1给出了用本文提出的局部干涉算法对不同刀位处进行检测的情况,其中θ代表了初始给定的刀具后倾角,θ终代表最终确定的最优刀具后倾角,tcal为检测需要的时间,这可以通过连续运行5000次取平均值来获得,采用C语言编程,在PC机(主频为1.8G,内存512M)上运算。

表1 一些刀位处的干涉检测情况
容易看出,在参数(u,v)等于(0.2,0.5)和(1.0,0.5)处,干涉没有发生,说明刀具后跟角θ还可以更小,以使刀具和工件曲面之间获得更好的几何匹配;而在参数(u,v)等于(0.4,0.5)、(0.6,0.5)和(0.8,0.5)处,经检测干涉已经发生,说明需要增大刀具后跟角才可以,θ终值能够真实的反映这个情况。同时,本文提出的干涉检测算法具有很高的计算效率,这五个刀位的平均检测时间为0.0078s。
5 结束语
在分析圆环面刀具五坐标端铣加工特性的基础上,本文提出了一种新的局部干涉检测算法。算法首先求得圆环面刀具环心圆到理想曲面之间的最小距离,然后将该距离与圆环面刀具的圆角小半径比较,从而判断局部干涉是否发生,并对发生干涉刀位通过调整刀轴矢量进行了处理。所提出的算法具有很高的计算效率,可以明显的节省计算机运行时间,具有较高的工程应用价值。
[1]陈松,姜虹,李学艺,等.自由曲面五坐标数控加工干涉检查[J].工程图学学报,2003(3):31-36.
[2]蔡永林,席光,樊宏周,等.曲面5轴加工中全局干涉检查与刀位修正[J].机械工程学报,2002,38(9):131-135.
[3]陈丽萍,陈燕,胡德金.非球头刀数控加工无干涉刀位的计算方法[J].上海交通大学学报,2004,38(7):1130-1133.
[4]严思杰,周云飞,陈学东,等.五轴NC加工干涉检查与避免算法研究[J].中国机械工程,2006,17(17):1822-1825.
[5]张和明,张玉云,熊光楞.复杂曲面五坐标数控加工干涉检查与刀位修正[J].清华大学学报(自然科学版),1998,38(2):65-68.
[6]彭芳瑜,周云飞,周济.复杂曲面的无干涉刀位轨迹生成[J].华中科技大学学报(自然科学版),2002,30(2):1-4.
[7]LEE Y S,CHANG T C.2-Phase approach to global tool interference avoidancein 5-axis machining[J].Computer-Aided Design,1995,27(10):715-729.
[8]高峰,吴俊军,王同洋,等.基于包容盒分解的快速干涉检验算法[J].计算机辅助几何设计与图形学学报,2000,12(6):435-440.
[9]许晓光.5坐标加工中干涉检测的凸包算法研究[J].航空精密制造技术,2008,44(6):28-32.
[10]杨方飞,阎楚良,林洪义.五轴数控加工叶片无干涉刀位轨迹的计算[J].农业机械学报,2003,34(2):97-100.
[11]姜虹,于源,王小椿.复杂腔槽五轴数控加工的干涉检查及修正算法研究[J].机械科学与技术,2007,26(3):274-278.
[12]龚堰珏,贠敏,王小椿.自由曲线曲面距离迭代算法的研究及其可视化处理[J].小型微型计算机系统,2003,24(12):2306-2308.

