基于灵敏度分析方法的渐开线直齿圆柱齿轮的疲劳强度研究

张 群，汪永超，黄娟娟，王小兵

(四川大学制造科学与工程学院，成都 610065）

0 引言

齿轮传动是机械传动中应用最广泛的动力和运动传递转置［1］，由于齿轮的制造成本较高，所以提高齿轮的寿命成为了一个很重要的研究课题。

齿轮的主要失效形式为轮齿的弯曲折断和齿面点蚀［2］，由计算模型知齿轮的结构参数是齿轮失效的主要影响因数。目前尚没有使用灵敏度分析法对影响疲劳强度的齿轮各结构参数进行灵敏度分析的文献。本文首次将灵敏度分析方法用于齿轮疲劳强度的研究中，以工程中一实用齿轮为例，采用Latin超立方采样作为输入，依据所建立的数学模型用五点插值数值微分法对齿轮的疲劳强度进行了灵敏度分析。分析结果揭示了齿轮各结构参数对疲劳强度的影响规律和敏感程度，为齿轮结构的优化设计提供了重要的理论依据。

1 渐开线直齿圆柱齿轮疲劳强度计算的数学模型

本文以渐开线直齿圆柱齿轮为研究对象，一般地，齿轮传动的失效主要是轮齿的失效:对于闭式齿轮传动，其主要失效形式为齿面点蚀和轮齿的弯曲折断，需要进行齿根弯曲疲劳强度和齿面接触疲劳强度计算;对于开式(半开式）齿轮传动，其主要失效形式为齿面磨粒磨损和轮齿的弯曲折断，由于目前尚无完善的磨损计算方法，因此通常只对其进行弯曲疲劳强度计算，并用适当加大模数的办法来补偿磨损的影响［2］。

根据文献［2］可知齿根危险截面的弯曲疲劳强度(弯曲应力）为:

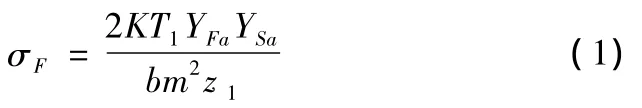
齿面的接触疲劳强度(接触应力）为:

式中:K为载荷系数;T1为小齿轮传递的转矩;b为齿宽;m为模数;z1为小齿轮齿数;YFa为齿形系数;YSa为应力校正系数;u为传动比;ZH为区域系数;ZE为弹性影响系数。

根据式(1）、式(2）知齿轮的疲劳强度与齿轮的结构参数齿宽b、模数m、小齿轮齿数z1有关。

2 灵敏度分析方法

齿轮的疲劳强度对齿轮各结构参数的灵敏度定义为齿轮的疲劳强度应力值对柔轮各结构参数的变化率，其几何意义是各结构参数对疲劳强度的敏感程度，绝对值越大表示越敏感。在结构优化设计中，通过灵敏度分析，可以确定调整何种设计参数最有效，从而选取尽量少的优化变量，降低优化设计的时间和工作量［3］。

若设影响齿轮疲劳强度的齿轮各结构参数X为:X=(x1，x2，…xk）T，齿轮疲劳强度应力值 σ 为:σ =f(X），则齿轮的疲劳强度灵敏度s为:

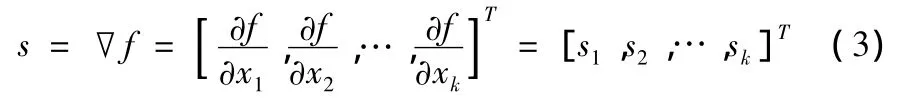
式中:si(i=1，2，…，k）表示齿轮疲劳强度对齿轮结构参数的灵敏度。

确定因素xi的灵敏度的过程如下［4-5］:令其他影响因素 x1，x2，…，xi－1，xi+1，…，xk不变，因素 xi在其值附近进行扰动(一般扰动范围为 ±10%），在因素xi的扰动范围内进行N次采样，并计算出各采样点的疲劳强度应力值fj(j=1，2，…，N），然后用五点插值数值微分法求出影响因素xi的灵敏度值，并拟合成灵敏度曲线，以此来反映影响因素xi对疲劳强度的敏感程度。

在计算疲劳强度应力值的过程中使用Latin超立方采样作为输入。Latin超立方采样产生受约束样本点的方法如下［6-7］:假设存在一个确定性的分析模型y=f(x），其中x= ＜ x1，x2，…，xn＞T代表输入变量向量，每个输入变量xi(i=1，2，…，n）由概率分布函数Fxi(x）描述。将每个输入变量xi的概率分布函数Fxi(x）的范围分割成N个不重叠的区间Sij(j=1，2，…，N），每个区间由概率表征:

并且有:

在抽样过程中，区间Sij由代表性参数代表，代表性参数有两种选择方法:一是在区间中随机选取，一是在区间中心处选取。

在区间中随机选取时，首先在(0，1）区间内生成N个随机数Qj，然后将其变换成第j个区间中的随机数Wj:

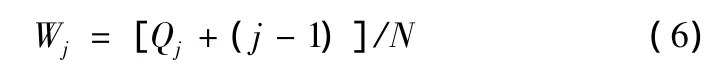
由式(6）可推得(j－1）/N ＜Wj＜j/N，其中(j－1）/N和j/N分别是第j个区间的下界和上界，因此每个区间上仅生成一个随机数Wj，求得约束随机数Wj后即可求得相应的随机变量为:

在区间中心处选取时，第j个区间的代表性参数可以由式(8）确定:

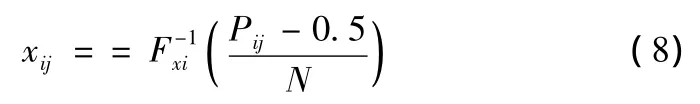
其中，Pij表示第i个输入变量xi的第j个模拟的区间秩数。

由采样过程知，在进行N次模拟以后，每个输入变量xi的N个观测值与一个随机排列的整数序列(整数1，2，…，N的随机排列）相联系，将n个变量的N次模拟的随机排列的矩阵记为R，R有N行n列。

上述抽样过程中矩阵R是随机产生的，各列间不可避免的会引入一定的统计相关，进而影响到灵敏度估计值的偏度和方差。Florian提出了一个减小统计相关的方法，用矩阵T来描述矩阵R各列间的统计相关，矩阵T中的元素Tuv(u，v=1，2，…，n）是R的第u和第v列间的Spearman系数，它定义为:

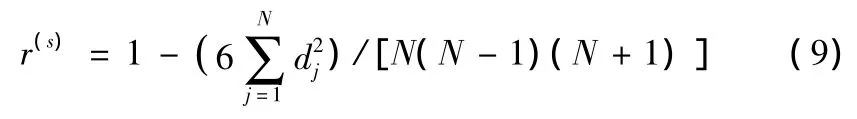
其中，dj是两样本的序差，N是样本数。显然矩阵T是对称的，且在各列不相关的情况下等于单位矩阵I。考虑到R的实现过程，T是正定矩阵，所以可以对T进行Chloesky分解:

其中，Q是一个下三角矩阵，QT是Q的转置，令S=Q－1，采用式(11）转换公式得到一个新的矩阵RB。

其中，RB各列间的统计相关由相关矩阵TB表示。由文献［8］的证明知TB比T更接近于单位阵，于是用矩阵RB代替矩阵R，可使随机排列表各列间的统计相关减小。于是将矩阵RB各列中的值通过式(6）、式(7）、式(8）的计算，可得输入样本{x}n。对此样本利用确定性的分析模型y=f(x）可计算输出变量的相应值。

将上述计算出的输出变量的相应值用五点插值数值微分法做数值微分，最后将求得的数值微分值拟合成曲线，以观察各参数的灵敏度。

3 实例分析

以一带式输送机减速器的高速级齿轮传动为例，对其齿轮的疲劳强度进行灵敏度分析。该减速器的基本参数如下:大小齿轮的材料均为45钢(调质），小齿轮齿面平均硬度为250HBS，大齿轮齿面平均硬度为210HBS，小齿轮传递的额定功率为P=9.2kW，小齿轮转速为n1=970r/min，小齿轮齿数z1=31，齿宽b1=84mm，大齿轮齿数z2=125，齿宽b2=78mm，模数m=2.5，中心距a=195mm。该减速器由电动机驱动，预计工作寿命为6年，每日工作16小时，带式输送机工作平稳，转向不变。

依据1中建立的数学模型，带入相应系数值，得疲劳强度与齿轮结构参数间的关系式为:

通过编程计算可得出各结构参数在其变化范围内的各采样点处的疲劳强度应力值，再对其进行五点插值数值微分计算，可得灵敏度值。为了直观的看到各结构参数在其变化范围内的灵敏度值和变化趋势，此处用灵敏度曲线来描述各结构参数对疲劳强度的影响程度，如图1～图6所示。

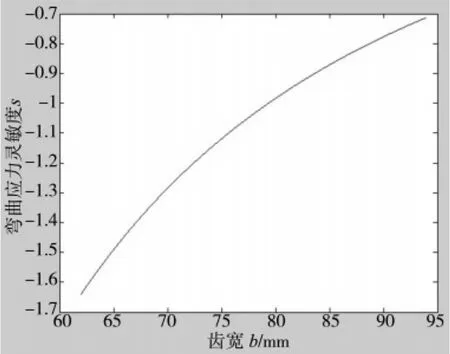
图1 齿轮齿宽灵敏度曲线

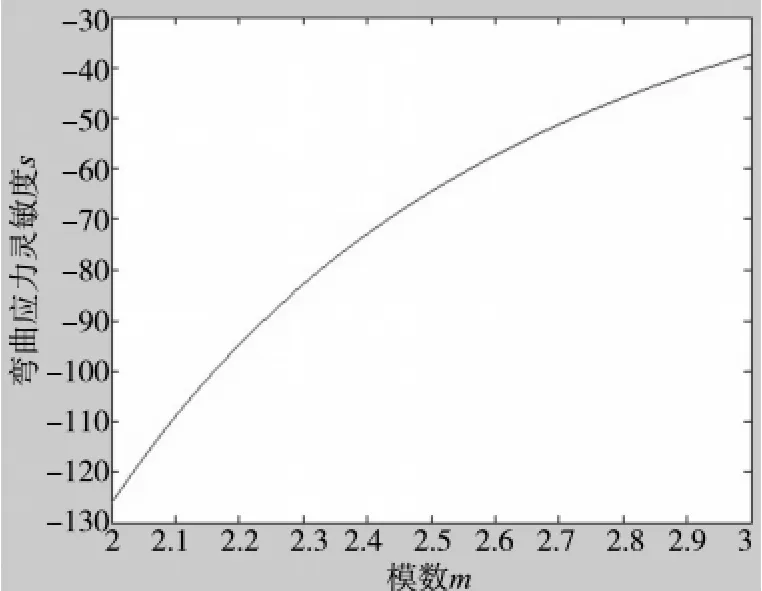
图2 齿轮模数灵敏度曲线

图3 齿轮齿数灵敏度曲线

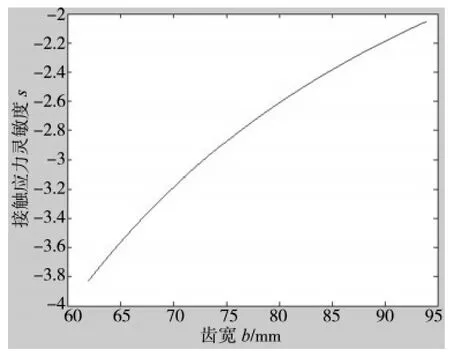
图4 齿轮齿宽灵敏度曲线

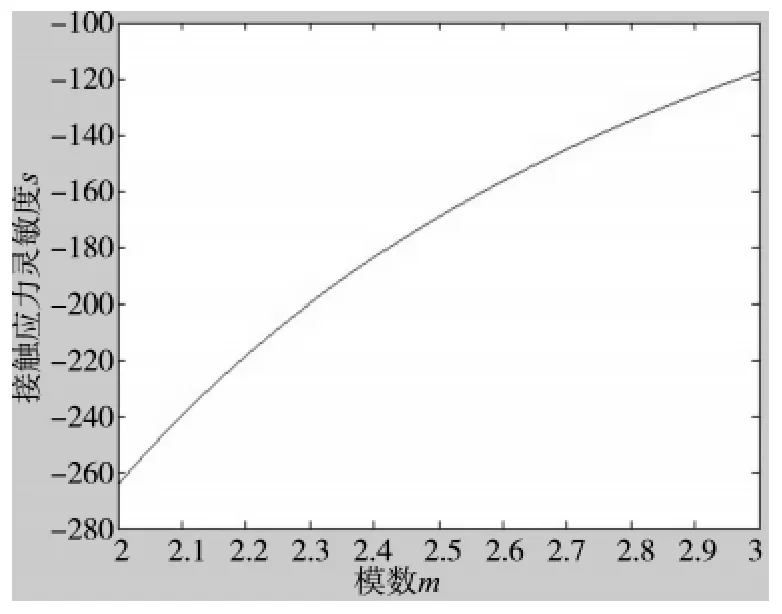
图5 齿轮模数灵敏度曲线

图6 齿轮齿数灵敏度曲线

从图1～图6可以看出:灵敏度值均为负值，且其绝对值随着齿轮各结构参数的增加而减小。由此得出齿轮各结构参数对疲劳强度的影响规律:随着齿轮各结构参数值的增加，弯曲应力和接触应力均减小，且减小速度在减慢，即齿轮各结构参数对疲劳强度的影响在减小。从图1～图6的纵坐标显示的灵敏度值的大小中还可以看出:无论是弯曲应力还是接触应力，模数对疲劳强度的灵敏度值远远大于其他两个参数对疲劳强度的灵敏度值，由此说明模数对疲劳强度的影响最显著即敏感程度最高，其次是齿轮齿数，敏感程度最低的是齿宽。

4 结束语

本文以渐开线直齿圆柱齿轮为研究对象，根据其疲劳强度计算的数学模型，首次采用灵敏度分析方法分析齿轮各结构参数对疲劳强度的敏感程度。本文在变量输入时采用Latin超立方采样，与传统的随机采样相比在结果精确度相同的情况下具有小的多的样本空间，提高了计算速度。在计算各输入点的灵敏度值时采用五点插值数值微分法，该方法比两点、三点插值数值微分法具有更高的精度。本文最后运用实例分析得出齿轮各结构参数对疲劳强度的影响规律，通过对灵敏度值的比较得出模数对疲劳强度的敏感程度最高，其次是齿数，敏感程度最低的是齿宽。该研究成果对齿轮结构的优化设计具有重要指导意义。

［1］袁文武，蔡慧林，任刚.基于UG和ADAMS的齿轮啮合动力学仿真［J］. 煤矿机械，2010，31(2）:40-43.

［2］谢江，娄晨辉，李兰.机械设计［M］.北京:国防工业出版社，2009.

［3］毛为民，朱石坚.隔振系统的灵敏度分析［J］.海军工程大学学报，2007，19(2）:68-71.

［4］竹振旭，董海军.基于灵敏度分析方法的摆线针轮系统传动精度研究［J］.机械科学与技术，2008，27(5）:644-648.

［5］韩林山，武兰英，沈允文.2K_V型减速机传动精度的灵敏度分析［J］.机械科学与技术，2010，29(10）:1366-1369.

［6］张令心，江近仁.Latin超立方采样技术及其在结构可靠性分析中的应用［J］.世界地震工程，1997，13(4）:1-6.

［7］万越，吕震宙.基于Latin方抽样和修正的Latin方抽样的可靠性灵敏度估计及其方差分析［J］.机械强度，2008，30(6）:927-934.

［8］Huntington D E，Lyrintzis C S，Improvements to and limitations of Latin Hypercube sampling［J］.Prob.Engng.Mech，1998，13(4）:245-253.