碳纤维木材复合材结合层剪切蠕变性能研究
杨小军,孙友富
(南京林业大学 木材工业学院,江苏 南京210037)
随着人们对居住环境质量要求的日益提高,现代木结构建筑业得到了迅猛发展[1],在建筑用天然林优质木材资源受到保护的今天,生长周期较短的速生材的结构化利用研究受到了人们普遍关注。中国速生落叶松Larix gmeinii资源丰富。落叶松生长周期短,纹理通直,结构均匀,在木材工业中的应用越来越广。其材质松软,密度低,强度小,易产生干缩变形,限制了其进一步的利用,特别是在建筑结构方面的应用。随着碳纤维增强复合材料(carbon fiber reinforced polymer/plastic,缩写为CFRP)技术的发展,在速生材表面粘结复合碳纤维布成了改善其性能一种有效的技术手段[2]。近年来,国内外也相继出现了大量采用CFRP加固建筑木梁、木柱及其节点加固的案例[3-4]。蠕变是碳纤维木材复合材用于结构用途时必须要考虑的重要因素之一。目前,有关碳纤维木材复合材蠕变的研究尚未见报道。本研究将从CFRP与木材结合层受剪性能入手,研究CFRP与木材间结合层蠕变特性,以指导CFRP在木结构加固工程中的合理应用。
1 材料与方法
1.1 试验材料
落叶松规格材,有部分活节,纹理通直,一等材,气干密度为0.632 g°cm-3,含水率为15%。CFRP布为聚丙烯腈基碳纤维,单向织物,理论厚度为0.111 mm,抗拉弹性模量为2.4×105MPa,面密度为206 g°m-2,抗拉强度为3 450 MPa,极限拉伸应变为1.0%;胶黏剂为双组分环氧类,混合后初黏度(23℃)为 5 000 mPa°s,其混合体积比为2︰1。胶体主要力学性能:抗拉强度50 MPa,弹性模量2.0 GPa,延伸率为2.2%,由南京某公司提供。
试验用主要设备为UTM 4304高低温持久蠕变试验机。
1.2 试验方法
试件设计如图1所示。木块尺寸为120 mm×50 mm×20 mm,为避免木块材面的差异皆取径切面作为粘结面,粘结面尺寸为20 mm×50 mm。木块端头预留10 mm,以减少因木块端头在负载时出现破损或变形而影响结合面。应力水平取平均极限剪切应力的20%,35%,50%和70%。试验环境取2个状态:①温度为24℃、相对湿度为45%(平衡含水率约为9.9%);②温度为60℃、相对湿度为90%(平衡含水率约为18%)。试验周期取12 h。
极限剪切应力:通过对20个试件的剪切拉断试验获得,平均极限剪切应力为2 286.25 N,变异系数为5.37%。
结合层厚度:通过改变复合CFRP时的压力(0.05 MPa以上)实现结合层不同厚度,以考察不同厚度层间蠕变关系。结合层厚度计算:H胶合层=H复合材-H木块-HCFRP,其中H指材料的厚度。
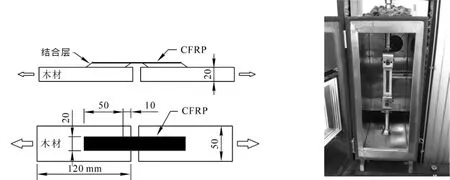
图1 试件设计及加载示意图Figure 1 Chart of samples’size and loading method
1.3 蠕变模型
碳纤维木材复合材结合层主要是具有黏弹性的环氧树脂胶体和木材表层。两者都为高分子材料,其应变行为可同时兼有弹性材料和黏性材料的特征[5-7],其蠕变变形通常由瞬间弹性变形、延迟弹性变形和黏性变形组成,将这三者串联起来便形成一个四元件模型,即Burger模型[8-10],如图2所示。本研究将采用Burger模型来描述复合材结合层黏弹性。
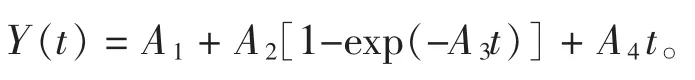
其中:Y(t)为随时间变化剪切变形的数学函数,A为待定系数,t为蠕变时间。A1和A4分别为弹性变形和黏性变形,A2和A3反映黏弹性变形。
2 结果与分析
碳纤维与木材间结合层剪切蠕变试验结果如图3所示。在4种应力水平下,各蠕变曲线变形规律几乎一致,都体现了初始蠕变阶段和等速蠕变阶段的短期特征[8-12]。
利用Burger蠕变模型公式作为回归方程表达式,分别进行了2种环境状态下各结合层蠕变特性曲线的数值拟合,方程各参数A1,A2,A3,A4值分别见图3。由图3可知:Burger模型描述结合层剪切蠕变数据比较精确,其相关系数都在98%以上,表明CFRP木材复合材结合层的短期剪切蠕变行为可用Burger模型来模拟。
由图3中试件2-1和试件2-2比较发现,在同样环境和同样的应力水平作用下,结合层厚度不同的试验中,厚度大的试件表现出较大蠕变变形量,试件2-2厚度增加23.5%,则初始变形及8 h蠕变值分别增加36.8%及29.7%。同样的剪切应变较厚结合层剪切位移大,另外,结合层厚易出现影响结合层应力分布均匀性的孔隙。厚度是影响结合层蠕变变形的重要因素,蠕变变形量大意味着应力松弛较快[5-6],特别是在较高应力水平。为减少结合层影响,可通过控制施胶量和施加压力的方法使结合层厚度降低。
不同环境状态下的试件1-1与试件1-2,试件3-1与试件3-2及试件4-1与试件4-2,瞬时弹性变形相差不大,但随着负载时间延续其蠕变变形量差距逐渐加大。这是由于蠕变试验时试件皆从室温环境状态逐渐向试验箱环境转变,即加载初期2个试件结合层几乎处于同一状态,瞬时弹性变形差异由结合层厚度引起。随着时间的延续,结合层胶体及木材表层逐渐适应于试验箱环境,高温高湿环境下木材吸湿,不可避免使结合层表层木材表现出机械吸湿蠕变现象,同时结合层胶体高分子热运动加剧,从而出现蠕变变形速率增加的现象。在高湿环境及70%应力水平下,结合层在465 min时便出现断裂,表明复合材结合层在高应力水平时耐温湿作用较差,在工程中应用时应避免将CFRP用于高温高湿环境或采取必要措施对结合层进行防护处理。
在不同应力水平下的试件1-1,试件2-1,试件3-1与试件4-1试件,蠕变变形差异较大但遵循相同的规律。在20%,35%和50%应力水平下,蠕变变形增加速率缓慢;而在70%应力水平下,蠕变变形增加速率明显高于其他应力水平,且发生蠕变破坏的可能性大大提高。高应力水平下以高温高湿环境蠕变变形速率增长最快,出现了在较短时间内破坏现象。为安全考虑,在应用时结合层设计应力水平应不超过50%。
模型参数A1反映在弹性范围内,剪力作用下结合层的抗变形能力,剪应力水平与A1比值几乎一致,结合层弹性性能与应力水平关系较小,在卸载后可完全恢复。A2及A3反映结合层黏弹性变形,图3中拟合数据可看出,A2及A3与应力水平及环境状态密切相关,应力水平越大或高湿环境下,其恢复原有尺寸的能力越来越小。A4反映结合层蠕变中的黏性变形,应力水平越大或高湿环境下,永久变形越大。

图2 Burger模型Figure 2 Burger model
3 结论
结合层蠕变变形都在相对短的时间内出现,且依赖于剪应力大小和负载时间。复合材结合层短期蠕变过程可分为2个阶段:第1级蠕变,蠕变以非线性方式增长;第2级蠕变,蠕变以低速率持续线性增长。
高温高湿环境下结合层蠕变量要显著大于低湿环境,高湿环境下,高应力水平易使结合层较早出现短裂,温度及相对湿度是影响蠕变的重要因素。

图3 结合层剪切蠕变拟合图Figure 3 Fitted data and chart of the bond layer’s shear creep
Burgers四元件模型可以用来模拟碳纤维木材复合材胶合层在高湿、低湿2种环境下短期剪切蠕变特性,其精度可以满足工程需要。
结合层厚度越大,剪切蠕变变形也越大,在保证胶合强度的前提下,建议碳纤维与木材复合时通过控制施胶量及施加压力(0.05 MPa以上)的方法来减小胶合层厚度。
蠕变变形随应力水平的增大而增大。各应力水平蠕变曲线都表现出了同样蠕变规律,蠕变变形在早期较大,后期逐渐减缓。蠕变测试时间不能充分反映材料的蠕变性能,今后还将进一步对材料的长期蠕变性能进行研究。
[1]周海宾,费本华,任海青.世界木结构房屋研究的最新进展[J].木材工业,2006,20(4):1-4.ZHOU Haibin,FEI Benhua,REN Haiqing.Evolutions of research on wood frame housing around the world [J].China Wood Ind,2006,20 (4): 1-4.
[2]周先雁,王兰彩.碳纤维复合材料(CFRP)在土木工程中的应用综述[J].中南林业科技大学学报,2007,27(5):26-32.ZHOU Xianyan,WANG Lancai.Summary of CFRP application in civil engineering [J].J Central South Univ For & Technol,2007,27 (5): 26-32.
[3]庄荣忠,杨勇新.FRP加固木结构的研究和应用现状[J].四川建筑科学研究,2008,34(5):89-92.ZHUANG Rongzhong,YANG Yongxin.Research and application on FRP in the reinforcement of timber structures[J].Sichuan Build Sci,2008,34 (5): 89-92.
[4]赵静,王鲲,牟晓成.CFRP材料加固木梁试验研究[J].山西建筑,2006,32(23):86-87.ZHAO Jing,WANG Kun,MOU Xiaocheng.Research on the test of strengthening wooden beam by CFRP materials[J].Shanxi Archi,2006,32 (23): 86-87.
[5]杨挺青.黏弹性力学[M].武汉:华中理工大学出版社,1990.
[6]王逢瑚.木质材料流变学[M].哈尔滨:东北林业大学出版社,1997.
[7]李大纲.意杨木材弯曲蠕变特性的初步研究[J].四川农业大学学报,1998,16(1):99-101.LI Dagang.A preliminary study of bending creep of Italy poplar [J].J Sichuan Agric Univ,1998,16 (1): 99-101.
[8]HUNT D G.The prediction of long-time viscoelastic creep from short-time data [J].Wood Sci Technol,2004,38 (2):479-492.
[9]HOYLE R J,GRIFFITH M C,ITANI R Y.Primary creep in Donglas fir beams of commercial size and quality [J].Wood Fiber Sci,1985,17 (3): 300-314.
[10]DEAN G D,BROUGHTON W.A model for non-linear creep in polypropylene [J].Polymer Test,2007,26 (8):1068-1081.
[11]SAMARASINGHE S,LOFERSKI J R,KOLZER S M.Creep modeling of wood using time-temperature superposition[J].Wood Fiber Sci,1994,26 (1): 122-130.
[12]RAFTERY G M,HARTE A M ,RODD P D.Bond quality at the FRP-wood interface using wood-laminating adhesives [J].Int J Adhes Adhesv,2009,29 (2): 101-110.

