基于小波熵的航空磁测数据去噪
谭斌,林春生,傅慷
(1.海军工程大学兵器工程系,湖北 武汉 430033;2.海军91458部队,海南 三亚 572021)
航空磁测是在大范围空间内对磁异常进行探测的有效方法,但各种干扰磁场和噪声降低了航空磁测的精度,虽然可以对飞机磁场和地磁日变进行补偿和改正,但补偿后剩余的干扰磁场以及磁探仪自身的噪声干扰,仍然导致无法对一些微弱的磁异常信号进行探测.因此,有必要对航空磁测数据进行去噪处理,提高测量数据信噪比.小波变换理论为噪声消除问题提供了一个新的思路.小波去噪中的关键问题是阈值的确定[1],目前主要有MAD(median absolute deviation)、MINIMAX(minimaland maximal value)、SURE(Stein’s unbiased risk estimate)和HYBRID(软硬阈值混合) 等方法[1-3]用于确定阈值.但这些方法在确定阈值时都带有一定的猜测性,因此去噪效果不稳定.
本文中结合信息论中熵的理论以及多尺度下小波熵的定义,在分析不同分解尺度上信号和噪声不同的能量分布特性基础上,通过对不同分解尺度上小波系数进行子带分解,计算不同子带分量的小波熵,利用最大小波熵自适应地选择阈值,利用最高一层小波分解的低频系数分量和经过阈值处理的不同尺度的高频小波系数分量对信号进行重构,实现航空磁测数据的有效去噪.
1 小波变换及小波熵
设x(t)是平方可积函数,即x(t)∈L2(R),则x(t)的小波变换为[4]:
(1)

(2)

(3)
相应小波变换为[4]
(4)
(4)式是离散小波变换(DWT),其输出结果是小波序列的系数djk,信号x(t)可用小波基函数和小波系数表示为[4]
(5)
由小波标架理论可知,当小波基函数是一组正交基函数时,小波变换具有能量守恒性质[5-7],即
(6)
此时,单一尺度下小波系数的平方和定义为该尺度下的小波能量[5-7],即
(7)
(8)
(9)

(10)
因此,信号熵值的大小反映了其概率分布的均匀性,即信号的概率分布越接近无序的分布,其熵值也就越大;反之其熵值就越小.如果把小波变换的系数矩阵处理成一个概率分布序列,则由它计算得到的熵值就反映了这个系数矩阵的稀疏程度,即信号概率分布的有序程度,这种熵就称作小波熵[5-7].如果将(10)式中的P(ai)换成(9)式中反映某一段信号能量强度比例的相对小波能量pj,则小波熵可定义为[5-7]
(11)
2 基于小波熵的阈值确定法
对于加性噪声模型,经过正交小波变换后,能最大程度地去除有用信号的相关性,将能量集中在少数稀疏的、幅度相对较大的小波系数上.而噪声对应的小波系数仍然互不相关,并将分布在各个尺度下的所有时间轴上,且幅度不是很大.如果在小波变换的各个尺度下保留那些集中了有用信号大部分能量的少数小波系数,而将其他点置零,或最大程度地减小,再利用处理后的小波系数做小波逆变换,就可实现对噪声的抑制.因此,小波阈值在去噪过程中起到了决定性的作用,将直接影响小波去噪的效果.
令经过补偿和日变改正航空磁测信号为x(n)=s(n)+u(n)
(12)

(13)
式中,MSE是均方误差,N是数据长度.

(14)

(15)
在阈值的确定过程中,将每一个分解尺度的高频信息量均看成一个单独的信号源,将每一层高频小波系数分成n个相等的小区间,计算各个小区间的小波能量,并计算各区间的小波能量与该尺度下的小波能量之比,将比值代入(11)式得到各区间的小波熵,选取熵值最大的那个小区间的中值作为该尺度下噪声的方差,再根据(15)式计算出各个尺度下的阈值.
3 去噪结果分析
3.1仿真去噪结果分析利用辛格函数模拟产生航空磁测中的地磁场异常信号,并用白噪声信号模拟航空磁测过程中的干扰磁场,两种信号合成仿真的航空磁测信号如图1所示.选用dB10小波基函数对仿真的航空磁测信号进行4层的多尺度分解,分别采用Rigsure阈值,Heursure阈值,MINIMAX阈值以及小波熵阈值进行小波去噪,最后利用经过阈值化处理后的小波系数进行重构,得到去噪后的航空磁测信号如图2所示.从图2中各种阈值去噪结果可以看出,基于Rigsure阈值、Heursure阈值和小波熵阈值的去噪结果较好,仿真航空磁测信号的噪声基本上都被去除,仿真地磁场异常信号得到较好的保留.表1给出了去噪前后仿真航空磁测信号和信噪比,通过对比可以发现,基于小波熵阈值去噪后的信号的信噪比增益最大.

图1 仿真信号

图2 仿真去噪结果
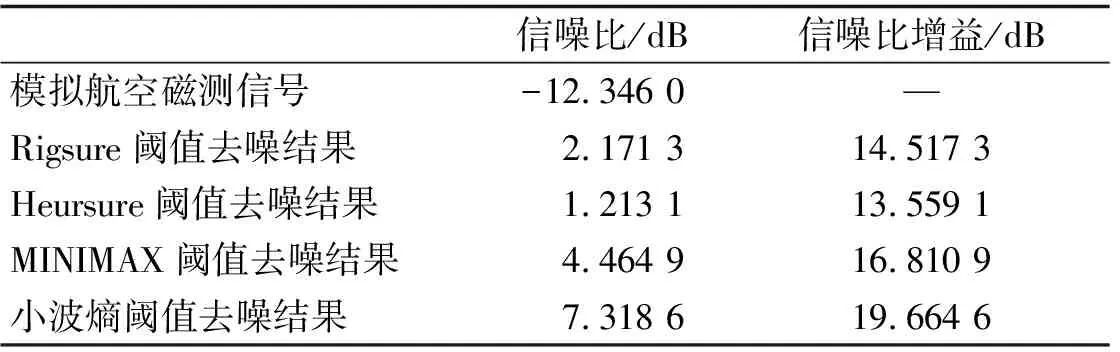
表1 仿真信号及去噪结果信噪比对比
3.2航空磁测数据去噪结果分析采用航空磁测飞行试验数据中一段长约100 s的磁异常探测数据,如图3所示.其中,在67 s处探测到一磁异常信号,从图中可以看出,磁异常信号被干扰磁场噪声污染,无法准确对噪声和磁异常信号进行分辨.选用dB10小波基函数对含噪的地磁场测量数据进行8层的多尺度分解,利用经过小波熵阈值化处理后的小波系数进行重构,得到去噪后的航空磁测数据.从图3中可以看出,经过去噪处理后,磁场测量数据中的噪声能够得到有效抑制,只剩下明显的磁异常场信号和一小部分残留噪声,从而实现对磁异常信号的探测与定位.

图3 航空磁测数据去噪结果
4 结论
本文中在小波阈值去噪的基础上引入小波熵概念, 通过对信号进行小波分解,计算各层目标信号和噪声的小波系数能量熵,利用信号在不同的分解尺度上具有不同的小波熵,自适应地确定高频系数的阈值.仿真试验与其它3种阈值方法去噪效果对比表明,基于小波熵的去噪方法能够获得更高的信噪比.在航空磁测数据去噪试验中,该方法能够有效抑制干扰噪声,提高微弱磁异常探测能力.
[1] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2004.
[2] Donoho D L, Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage[J].Journal of the American Statistical Association,1995,90(432):1200.
[3] DONG Y S, YI X M.Wavelet denosing based on four improved function for threshold estimation [J].Journal of Math,2006,26(5):473-477.
[4] 吴正国,夏立,尹为民.现代信号处理技术[M].武汉:武汉大学出版社,2003.
[5] Svaldo A R,Susana B.Wavelet entropy:a new tool for analysis of short duration brain electrical signals [J].Journal of Neuroscience Methods,2001,105:65-75.
[6] 高建波,杨恒,胡鑫尧,等.基于最大熵原理的小波去噪方法[J].光谱学与光谱分析,2001,21(5):620-622.
[7] 张引红,李全禄.基于小波熵的鼾音信号去噪处理[J].计算机工程与应用,2011,47(30):19-22.
[8] 傅祖芸.信息论—基础理论与应用[M].北京:电子工业出版社,2001.
[9] Donoho D L,Johnstone I M.Ideal denoising in an orthogonal basis chosen from a library of bases [J].C R Acad Sci I-Math,1994,319:1317-1322.
[10] Jansen M.Noise reduction by wavelet thresholding [M].New York:Springer-Verlag,2001.

