煤储层参数测井定量计算方法探讨

杨克兵, 钱 铮, 孙守刚, 焦双志 严德天

(中石油华北油田分公司勘探开发研究院，河北 任丘 062552)

煤储层参数测井定量计算方法探讨

杨克兵, 钱 铮, 孙守刚, 焦双志 严德天

煤层气已进入大规模开发阶段，但相关的煤储层参数定量计算还有许多不足之处，达不到应用效果。以试验分析资料为依据，提出了使用自然伽马相对值计算煤岩组分、使用可变的煤岩骨架值计算孔隙度、使用电阻率校正方式进行含气量计算的煤储层参数计算方法。研究结果表明，上述方法适合于应用测井资料进行逐点数字处理，提高了参数计算的精度，能够满足实际使用要求。

煤层气；煤组分；孔隙度；含气量；定量计算

煤储层的重要参数有固定碳、灰分、挥发分、水分、孔隙度、渗透率、含气量、镜质体反射率、有效厚度等，是研究煤层组分和评价煤层气的地质勘探、工业分析及有效开发的依据。上述参数一般由钻井取芯后对煤层岩心进行实验测定得出，但随着煤层气区块的规模开发，大量单井煤储层参数的评价只能由测井资料进行计算求取[1-2]。由于煤储层的非均质性及煤岩成份的复杂性与可变性，煤层低孔、低渗，微孔隙发育，而且煤岩骨架参数是变化的[3]。因此，应用常规测井资料定量评价煤储层参数有一定难度。经过多年研究，人们提出了一系列进行煤储层参数半定量、定量评价的方法[4-6]，但煤储层部分参数的计算结果在实际应用中不尽人意。为此，笔者通过对山西沁水盆地郑庄、樊庄区块煤心实验数据进行统计，结合测井响应特征，在考虑煤岩骨架参数变化的基础上，建立了一套煤储层组分及孔隙度定量计算方法。此外，对含气量的计算考虑了电阻率的影响，提出了依据电阻率对含气量进行校正的方法。

1 煤组分计算方法

煤岩组分划分为固定碳、灰分、挥发分、水分，根据试验分析结果，煤岩组分固定碳、灰分相互间有较好的关系，其中灰分与固定碳之间相关性较高，相关系数(R)都在0.9以上[4]。数据显示(见图1)，随着灰分含量增加，固定碳含量降低，挥发分含量缓慢增大，而水分含量变化不大。灰分与固定碳+挥发分之间的相关性最高，相关系数接近1。因此，只要计算出灰分含量，其他组分含量都可依据经验公式推出，这为测井计算煤岩组分含量提供了依据。

图1 某区块井煤层工业组分试验数据关系图

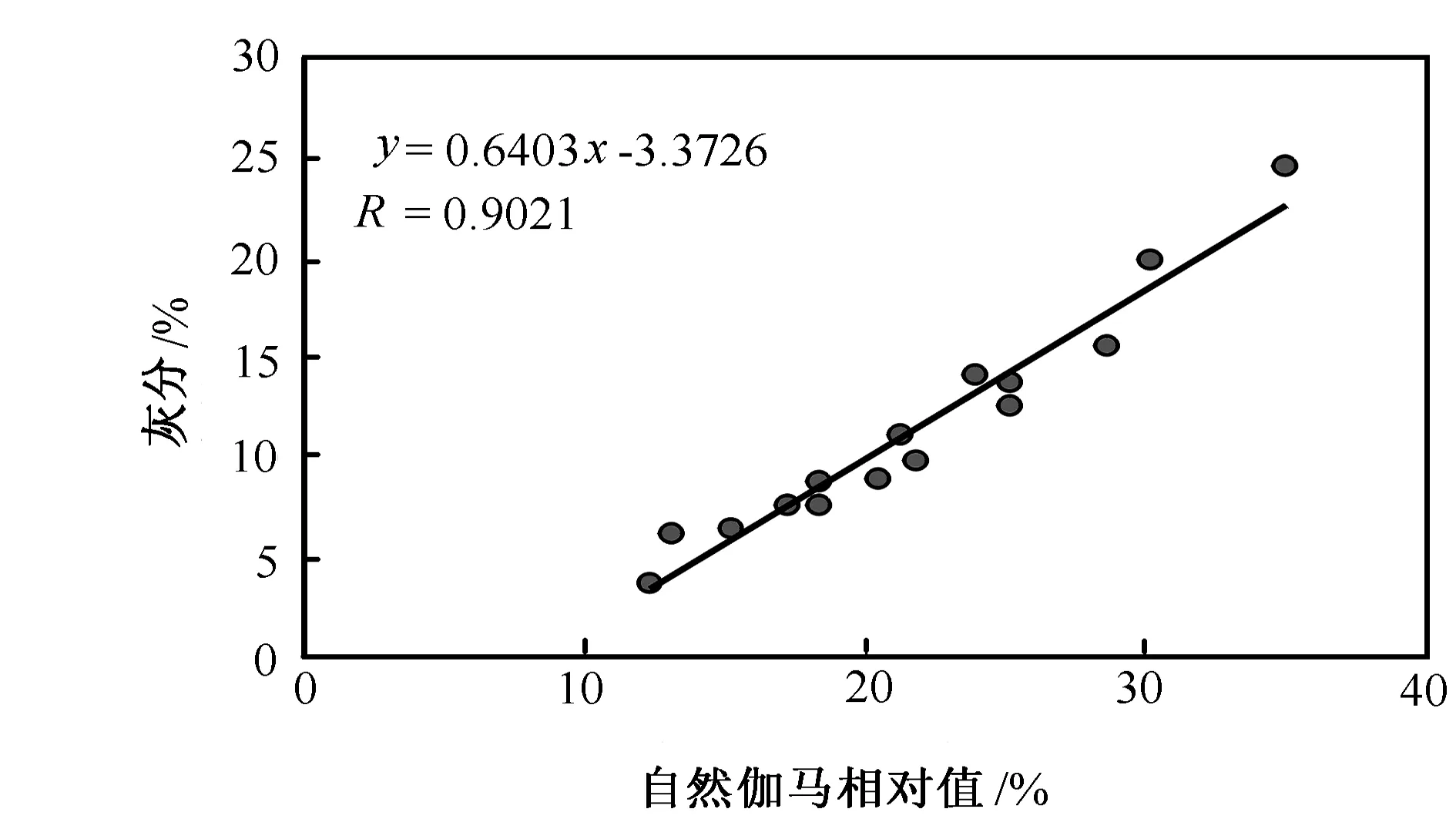
图2 灰分含量与自然伽马相对值关系图

由于灰分含量与自然伽马测井值具有较好的相关性，因此，根据自然伽玛曲线通过回归公式计算灰分含量，是当前计算灰分含量的一种主要方法。由于不同区块、不同煤阶的煤岩计算公式有一定区别，因而应对自然伽马曲线进行标准化校正后才能应用。为了能够对不同区块、不同煤阶的计算公式进行统一处理，可以通过采用自然伽马相对值与灰分含量建立回归关系的方法来解决这一问题(见图2)。

表1所示为研究区块某井的计算实例，计算结果与试验分析数据的误差在3%以内，能够满足使用要求。

表1 利用自然伽马相对值计算煤岩组分与岩心试验分析组分对比

2 煤层孔隙度计算方法

煤层基质孔隙度计算一般采用声波时差的平均时间公式[5]：

Φ=(Δt-Δtma)/(Δtf-Δtma)

(1)

式中，Φ为煤层孔隙度；Δt为煤层声波测井值，μs/m；Δtma为岩石骨架声波时差，350～430μs/m；Δtf为流体声波时差，620μs/m。

此外，还可由中子、密度公式等计算求取平均值作为煤储层的孔隙度，上述计算公式都要遇到煤岩骨架值的确定问题。图3是研究区块煤岩岩心分析孔隙度与声波时差交会图，可以看出，数据点的相关性较差，其原因是煤岩骨架声波时差是变化的。当部分煤岩骨架声波时差有变化时，影响了整体数据的相关性。在逐点处理的实际计算中，可能煤岩每点的骨架时差都是有变化的。一个层采用固定的骨架值，无疑使孔隙度的计算产生了较大的误差。因此，准确确定煤岩骨架值，是用常规测井资料计算煤储层孔隙度的关键。

图3 煤岩孔隙度与测井声波时差关系图 图4 煤岩骨架声波时差与密度测井值关系图

根据声波公式并使用岩心分析资料反算煤岩骨架声波时差，再与其他测井曲线中子、密度等建立回归关系，发现其与煤岩的密度测井值有较好的相关性(见图4)。因此，计算孔隙度时先采用煤岩密度测井值计算煤岩骨架密度，再用上述公式计算煤岩孔隙度可取得较好效果(见表2)。从表2可以看出，计算的孔隙度误差在2%以内，可以满足测井计算孔隙度的误差要求，这样在没有试验分析资料的地区，通过煤岩测井计算孔隙度具有可操作性。

表2 利用密度声波时差综合计算孔隙度与岩心试验分析孔隙度对比表

3 含气量计算方法

煤层气在煤储层内的赋存状态以吸附气为主，加上割理裂缝系统少量游离气。因此，含气量是指吸附气含气量，对于一般封堵性好的煤层而言含气量是饱满的。由于需要评价的是煤储层吸附气，实际上是评价饱含气煤储层的含气量。对测井曲线而言，识别煤层很容易，但煤岩含气量的变化并没有引起测井曲线明显的反映，相关测井数据对吸附气的反映较弱。由此可知，要准确评价计算煤储层含气量，首先要能评价煤层饱含气时的含气量，其次依据煤储层的保存情况进行适当校正。根据单井的资料情况，发现岩心测量含气量低的煤储层电阻率曲线明显降低，其主要原因是煤层水洗导致含气量降低，故在电阻率曲线上有所反映。但煤储层电阻率的变化范围较大，约(10～20000)Ω·m，采用类似含水饱和度的计算方法来计算含气饱和度，相关参数难以确定，因而可以考虑引入电阻率数据对含气量进行校正。

依据前人研究成果，煤层含气量与煤层的厚度、煤的热演化程度、煤层深度、温度和压力等参数有密切的关系[6]。由于煤的内表面积大，储气能力高，煤层比相同体积的常规砂岩多储1～2倍以上的天然气，相当于孔隙度为30%的砂岩含水饱和度为零时的储气能力[1]。据此应用气体状态方程和煤层密度计算包含气层煤储层含气量：

P1V1=RT1P2V2=RT2

则：

V1=T1P2V2/ (P1T2)Q=V1/DEN

式中，P1为地面压力，MPa；V1为地面气体体积，m3；T1为地面绝对温度，℃；P2为地下深度压力，MPa；V2为煤孔隙度按30%计算的气体体积，m3；T2为地下深度的绝对温度，℃；R为气体常数；DEN为煤体积密度，t/m3；Q为煤层含气量，m3/t。

利用上述计算式对晋试1井煤层的含气量进行计算，其中3号煤层计算平均含气量为21.71m3/t，该层有6块岩心提供试验测定含气量在12.1～27.2m3/t之间，平均为22.07m3/t，说明计算值与试验测定值的误差较小。此外，由于煤层含气量变化与煤层电阻率的大小有关，因而对上述公式计算结果应根据煤储层电阻率的变化进行校正，从而取得更好的效果。根据该研究区块的试验分析资料，采用如下校正公式：

Q=aV1/DEN

式中，a为校正系数，通过计算V1/DEN与log(Rt)和试验测定的含气量回归确定。

表3所示为某井计算含气量与岩心试验分析含气量对比表。从表3可以看出，计算含气量随电阻率变化，与试验测定值匹配较好，绝对误差一般控制在3%以内，最大不超过4.26%，能满足实际使用要求。

4 结 论

1)在使用自然伽马相对值进行回归的情况下，计算的煤岩组分参数与岩心分析资料吻合较好，具有实际推广使用价值，对今后该类参数的求取提供了一条较好的解决办法。

表3 某井岩心试验分析含气量与计算含气量对比

注：RLL8为八侧向电阻率；RILM为中感应电阻率；RILD为深感应电阻率；GR为自然伽马；DEN为地层密度；AC为声波时差；CNL为补偿中子孔隙度。

2)采用密度测井资料计算煤岩的骨架声波，再用声波公式计算煤岩孔隙度，使得煤岩孔隙度的计算精度大大提高。

3)对含气量的计算应综合考虑煤岩埋深、物性、密度等参数的变化，并结合电阻率参数来进行逐点数字处理，最终可提高测井资料计算含气量参数的精度。

[1]赵庆波,刘兵,姚超.世界煤层气工业发展现状[M].北京:地质出版社，1998.

[2]陈永武,胡爱梅.中国煤层气产业形成和发展面临的机遇与挑战[J].天然气工业，2000，20(4):19-23.

[3]蔚远江,杨起,刘大锰，等.我国煤层气储层研究现状及发展趋势[J].地质科技情报，2001，20(1):55-60.

[4]侯俊胜.煤层气储层测井评价方法及其应用[M].北京:冶金工业出版社，2000.

[5]洪有密.测井原理与综合解释[M].东营:中国石油大学出版社，2008.

[6]杨东根,范宜仁,邓少贵，等.利用测井资料评价煤层煤质及含气量的方法研究[J].勘探地球物理进展，2010，33(4):262-265.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.06.016

P631.8

A

1673-1409(2012)06-N048-03