储罐液体晃荡问题的有限元分析

贾善坡，赵友清，许成祥 朱成安 谭继可

(长江大学城市建设学院，湖北 荆州 434023)(中石油唐山液化天然气项目经理部，河北 唐山 063000)(长江大学城市建设学院，湖北 荆州 434023)

储罐液体晃荡问题的有限元分析

贾善坡，赵友清，许成祥 朱成安 谭继可

(长江大学城市建设学院，湖北 荆州 434023)(中石油唐山液化天然气项目经理部，河北 唐山 063000)(长江大学城市建设学院，湖北 荆州 434023)

采用有限元方法数值求解了任意容器内液体晃动的固有频率、模态和地震响应动力学问题。基于液体晃动的泛函极值原理，在晃动自由面上忽略液体的表面张力，对液体晃动有限元方程进行静态缩聚，计算了矩形容器内液体晃动的特征频率，并与解析解进行比较。研究表明，利用该方法计算的结果具有较高精确度，可以为研究储罐晃动动力特性分析提供参考。

液体晃动；有限元法；充液容器；地震响应

晃荡是指部分充满液体的容器在外部激振力的作用下产生可自由移动的自由表面的现象，它是一种非常复杂的流体运动，呈现出很强的非线性和随机性。液体的晃动问题在石油化工设备、高层建筑减振、城市供水、船舶等领域均有应用，具有广泛的工程背景[1-2]。储罐、液体储槽及水塔等地面设备在地震中由于内部所储存液体的剧烈晃动而遭破坏；在罐装汽车行业中，必须要对液化气体、石油、化学剂等的大型液体运输罐进行晃动分析；在船舶工程领域，船舶被用来运输大量液体，大体积液体的晃动对船舶结构稳定性的影响尤为突出[3]。容器液体晃动和控制问题的研究受到众多研究人员的广泛重视，李遇春等[5]利用边界元方法对液体非线性晃动问题进行了数值分析；包光伟等[6]采用VOF方法对液体晃动进行了数值仿真；周宏等[7]采用ALE方法对带有自由液面的晃动问题进行了分析讨论；尚春雨等[8]提出用FLUENT计算液体晃动问题的方法；李青等[9]推导了任意三维贮箱内液体晃动的等效力学模型，采用有限元方法建立计算等效力学模型参数的数值算法，并采用商用分析软件FLOW-3D 验证了等效力学模型的有效性。下面，笔者基于液体晃动的泛函极值原理，采用静态缩聚技术，进而提出了储罐流体晃动特征问题的有限元计算方法。

1 基本方程

将储罐容器壁简化为刚性，把储液看成无旋和不可压缩流体，则液体在域V内满足连续性方程和Euler水动力学方程，在容器湿表面∂Vw(固壁边界)上满足不可渗透性条件，在自由面∂Vf(自由面边界)上满足运动学边界条件和动力学边界条件。设液体的速度势为Φ(x,y,z)，则Φ液体在域V满足如下方程[10]：

▽2Φ(x,y,z)=0

(1)

在容器壁面和自由表面上满足的边界条件如下：

(2)

式中，g是重力加速度；∂Vw、∂Vf分别是壁面边界、自由面边界。

令Φ(x,y,z)=iωφ(x,y,z)eiωt，代入式(1)和式(2)，构造如下泛函：

(3)

将液体域V上的解函数写成如下形式：

(4)

式中，Nj(x,y,z)为流体单元形函数；φj为单元节点变量。

将式(4)代入泛函表达式(3)，则泛函成为节点变量(φ1,φ2,…,φn)的函数，即：

Ψ=Ψ(φ1,φ2,…,φn)

(5)

求解泛函极值问题等价于求解下列方程组

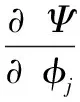
(6)

的解(φ1,φ2,…,φn)，从而确定液体域V上的解函数(4)。

2 液体晃动问题的有限元模型

液体晃动的有限元方程为：

(7)

式中，Φ为液体节点速度势阵；M为流体质量阵；K为流体刚度阵；F为流体力矢量阵。

将Φ写为Φ=[Φ1,Φ2]，其中，Φ1、Φ2分别对应于自由液面节点和液体域节点，则式(7)可写为：

(8)

对于液体晃动问题，系统的自由度相当多，计算费时且求解困难，因而采用静态凝聚技术对流体晃动计算问题进行简化[11-12]。

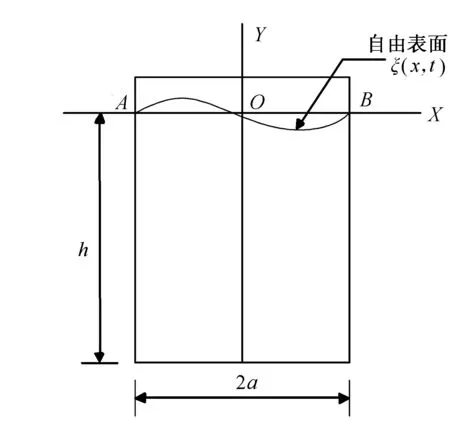
图1 矩形容器示意图

由式(7)可以发现，式(1)为拉普拉斯方程，对质量阵M无贡献，只有自由液面边界条件对质量阵M有贡献，故M12=M22=0，而M11正是自由液面边界条件对质量阵的贡献。对式(8)进行静态缩聚，可得到：

(9)

3 计算实例

选取二维矩形容器(见图1)内液体晃动问题作为计算实例，相关参数如下：容器宽度2a=3m，充液深度h=4m，液体密度ρ=1000kg/m3。

假定容器内的液体是无旋和不可压缩的，则液体晃动的自然频率解为[13]：

(10)

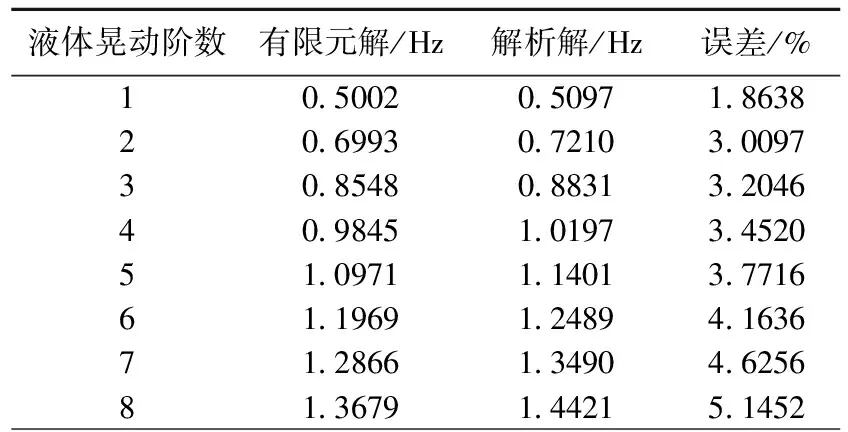
表1 有限元解与解析解的比较

3.1液体自由晃动分析

液体自由晃动分析的数值解和理论解如表1所示。从表1可以看出，流体晃动前7阶频率的误差一般控制在5%以内，说明利用该方法分析的误差较小。

图2 矩形容器前6阶液体晃动模态图

3.2地震响应分析

输入El-Centro地震波，其最大峰值加速度为35×10-2m/s2，时间为40s，El-Centro地震波波形如图3所示，液体在地震激励El-Centro波作用下自由液面中点O的液面晃动高度随时间的反应曲线如图4所示(液体晃动波高的数量级为10-8，接近于不晃动状态)。

自由液面中点A处液面波高时程曲线如图5所示。由图5可知，在El-Centro地震荷载作用下，点A处液面的晃动波高在t=12.78s时达最大值(0.120m)。自由液面中点B处液面波高时程曲线如图6所示。由图6可知，在t=5.37s时，点B处液面晃动的最大波高为0.148m。同时,可以看出，点A处与点B处的晃动形态相反，并且液体晃动具有明显的非线性性能。

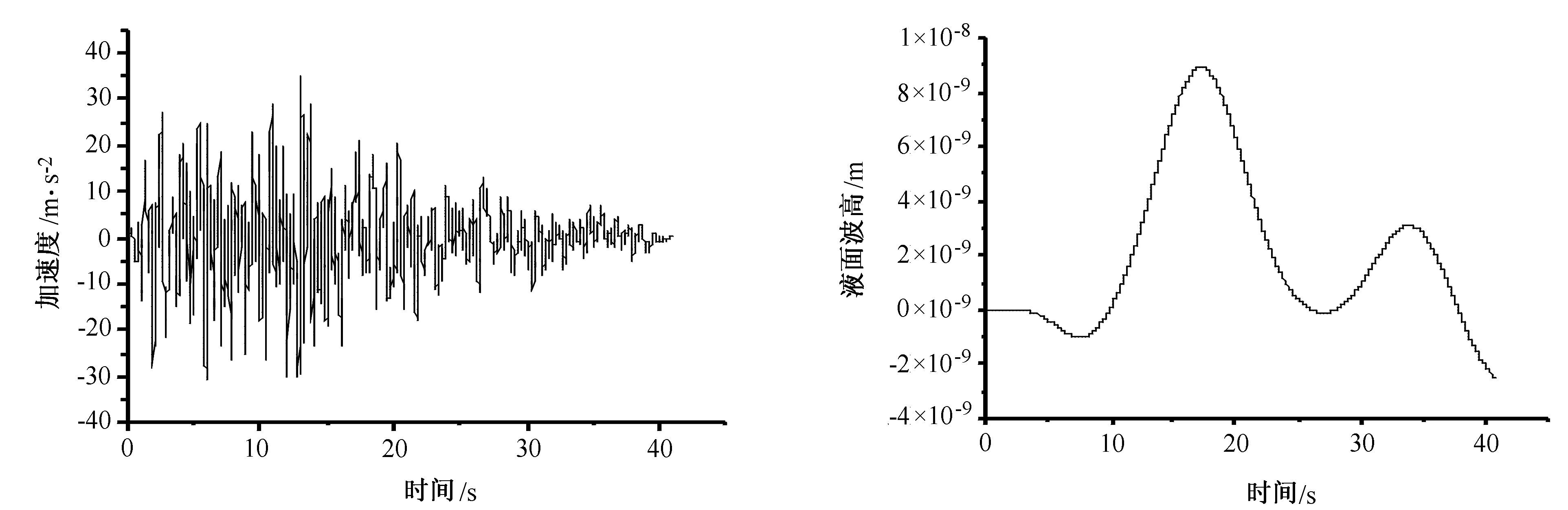
图3 El-Centro地震波时程曲线 图4 自由液面点O处液面波高时程曲线

图5 自由液面中点A处液面波高时程曲线 图6 自由液面中点B处液面波高时程曲线

4 结 语

采用有限元法建立了任意充液容器内液体晃动问题的数值计算方法，研究中假定容器壁面是刚性的，在晃动自由面上忽略了液体的表面张力，采用静态缩聚技术来了解容器内液体的晃动动力特性，并通过算例验证了该方法的正确性。该方法可适于分析二维和三维等复杂形状容器内液体的晃动问题，但对流固耦合问题，特别是抑制防晃问题以及流体-储罐-地基相互耦合问题有待进一步研究。

[1]贾善坡,许成祥.储液容器内液体自由晃动的有限元分析[J].船舶力学, 2012, 16(1-2):21-26.

[2]许成祥,贾善坡.储罐结构有限元动力模型修正及参数辨识研究[J].武汉理工大学学报,2010,32(9):286-290.

[3]岳宝增,祝乐梅,于丹.储液罐动力学与控制研究进展[J].力学进展, 2011,41(1):79-92.

[4]王照林，刘延柱.充液系统动力学[M].北京:科学出版社，2002.

[5]李遇春,楼梦麟.渡槽中流体非线性晃动的边界元模拟[J].地震工程与工程振动,2000,20(2):51-56.

[6]包光伟,王振强,张天翔,等.火箭推进剂液体晃动关机响应的数值仿真[J].宇航学报,2002,23(2):84-88.

[7]周宏,李俊峰,王天舒.用ALE有限元模拟的网格更新方法[J].力学学报,2008,40(2):267-272.

[8]尚春雨,赵金城.用FLUENT分析刚性容器内液面晃动问题[J].上海交通大学学报,2008,42(6):953-956.

[9]李青,马兴瑞,王天舒.非轴对称贮箱液体晃动的等效力学模型[J].宇航学报,2011,32(2):242-249.

[10]LIU Dongming,LIN Pengzhi.A numerical study of three-dimensional liquid sloshing in tanks[J]. Journal of Computational Physics,2008,227: 3921-3939.

[11]赵玉成，张亚红，白长青，等.固体火箭发动机模态分析的缩聚方法[J].固体火箭技术,2004，27(2)：98-100.

[12]朱安文，曲广吉，高耀南.航天器结构动力模型修正中的缩聚方法[J]. 中国空间科学技术，2003(2)：6-10.

[13]梅强中.水波动力学[M].北京：科学出版社，1984.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.11.035

TE972 107

A

16731409(2012)11N10703